AP Calculus AB Exam Answers and Solutions

The journey to mastering advanced mathematics requires both strategic study and focused practice. The key to success lies not only in understanding fundamental concepts but also in applying them efficiently under timed conditions. Preparing for this challenging assessment involves honing problem-solving skills, familiarizing oneself with question formats, and practicing with real-world examples.
Success in this test requires more than just memorization–it demands the ability to think critically and analytically. Recognizing patterns, applying formulas, and solving complex problems quickly are essential skills that contribute to a high score. In this section, we will explore various methods to prepare for the test, including detailed strategies for answering different types of questions and key topics to focus on.
Whether you’re revising for the first time or aiming to refine your skills, understanding the structure and expectations of the test will allow you to approach each question with confidence. The following tips and techniques will help you improve your performance and ensure you’re fully prepared for the challenges ahead.
AP Calculus AB Exam Overview
This test is designed to assess your ability to solve complex mathematical problems and apply critical thinking to various scenarios. It evaluates your knowledge of foundational principles, as well as your ability to manipulate mathematical concepts in both theoretical and applied contexts. Success on this assessment requires a comprehensive understanding of key topics, along with the ability to perform under timed conditions.
The structure of the assessment includes multiple sections that require different strategies and approaches. To prepare effectively, it is important to understand the types of questions you will encounter and how they are weighted. The test consists of two main parts: multiple-choice questions and free-response questions, each testing distinct skills.
- Multiple-choice section: Focuses on quick problem-solving and conceptual understanding. It is important to read each question carefully and eliminate incorrect options to maximize your score.
- Free-response section: Tests your ability to explain your reasoning and work through problems in detail. This section requires clear, logical steps and thorough justification for each solution.
Each part of the test is weighted to reflect the relative importance of different topics, and the scoring is designed to reward both accuracy and depth of understanding. Being familiar with the structure and timing of each section will help you manage your time effectively and improve your performance.
Understanding the Exam Format
The structure of this assessment is designed to test both your theoretical knowledge and practical problem-solving skills. The test is divided into two main components, each targeting different aspects of your mathematical abilities. Understanding how each section works and how to approach them is crucial for success.
The first component consists of multiple-choice questions. These questions require quick thinking and the ability to apply concepts in a time-constrained environment. You’ll need to interpret each problem carefully and use your knowledge to select the correct answer from the given options. This section tests both your speed and accuracy in solving mathematical problems.
The second part of the test focuses on free-response questions. Here, you are expected to show your work in detail and explain your reasoning step by step. This section evaluates your ability to approach problems methodically, break them down into solvable steps, and present your findings in a clear and logical manner. It is essential to demonstrate not only the correct solution but also the process used to arrive at it.
Key Topics Covered in AP Calculus AB
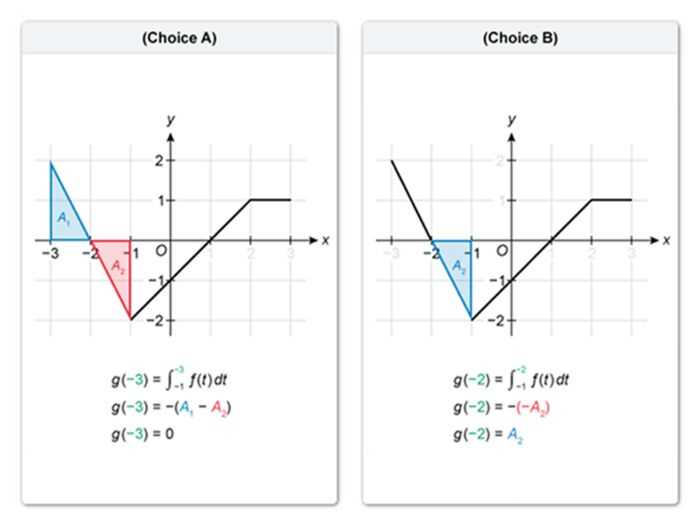
This assessment covers a broad range of mathematical concepts, each designed to test your understanding of core principles and your ability to apply them in different contexts. The key topics focus on fundamental concepts of functions, limits, derivatives, and integrals. Mastery of these areas is essential for performing well on the test, as they form the foundation for the majority of questions.
The table below outlines the main areas of focus, highlighting the core concepts and skills you need to be familiar with:
| Topic | Description |
|---|---|
| Functions and Graphs | Understanding different types of functions and their graphs, including linear, polynomial, exponential, and trigonometric functions. |
| Limits and Continuity | Exploring the behavior of functions as they approach specific values and understanding the concept of continuity. |
| Derivatives | Calculating and interpreting derivatives, including rules for differentiation and applications like velocity and optimization problems. |
| Integrals | Understanding integration techniques, including definite and indefinite integrals, and their applications in areas such as area under curves. |
| Fundamental Theorem of Calculus | Connecting differentiation and integration, and understanding how to apply this theorem in problem-solving. |
These topics are integral to the structure of the test, and a strong grasp of each will help you navigate the different sections with confidence. Focus on building a solid foundation in these areas to ensure success in the assessment.
How to Approach Multiple-Choice Questions

Multiple-choice questions are designed to assess your ability to quickly apply concepts and solve problems accurately. These types of questions require a strategic approach to ensure you maximize your score while managing your time effectively. Understanding how to tackle these questions can significantly improve your performance and reduce the likelihood of making mistakes.
Here are some key strategies to help you navigate multiple-choice questions with confidence:
- Read the question carefully: Make sure you fully understand what is being asked before you look at the answer choices. Pay attention to key terms and conditions in the problem.
- Eliminate obviously incorrect answers: Start by crossing out answers that are clearly wrong. This increases your chances if you need to guess later.
- Look for clues in the question: Sometimes, the wording of the question or the structure of the options can give you hints about the correct answer.
- Don’t rush: Take your time to consider each option carefully. Rushed decisions are often incorrect. If you’re unsure, move on and return to the question later if time permits.
- Check for consistency: Ensure that your chosen answer makes sense in the context of the problem. Double-check that the calculations or reasoning behind it align with the question’s conditions.
- Use estimation: If you’re stuck, try estimating the answer by working through the problem mentally. Often, rough calculations can help guide you to the right choice.
By applying these strategies, you can approach multiple-choice questions with greater precision and reduce unnecessary mistakes. Practice with sample questions can further refine these techniques and enhance your ability to make quick, informed decisions under pressure.
Free Response Question Strategies

Free-response questions require a deeper level of analysis and problem-solving than multiple-choice questions. These questions ask you to demonstrate your thought process and provide detailed explanations for your solutions. A well-organized and clear response can significantly impact your score, as this section evaluates not only your ability to find the correct answer but also how you approach and articulate each step.
Break Down the Problem Step by Step

Start by carefully reading the problem and identifying the key components. Break the problem into smaller, manageable parts and solve each part one at a time. This approach helps you stay organized and ensures that you don’t overlook important details. As you work through the steps, write out each stage of your reasoning clearly, even if it seems obvious. This will help ensure you get full credit for your method.
Show All Work and Justify Your Steps
In free-response questions, showing your work is just as important as finding the correct answer. Be sure to explain your reasoning and provide all necessary calculations, including intermediate steps. Avoid skipping steps, even if they seem simple. Each part of your process contributes to your overall score, so make your logic easy to follow and well-supported.
By following these strategies, you can improve the clarity and completeness of your responses, ensuring that you showcase both your problem-solving skills and your ability to communicate mathematical reasoning effectively.
Time Management Tips for the Exam
Effective time management is crucial when preparing for and taking this type of assessment. With a limited amount of time to complete all sections, it’s important to stay organized and prioritize tasks efficiently. By managing your time wisely, you can ensure that you have enough time to work through every question and still review your answers before submitting.
Here are some key strategies to help you make the most of your time during the test:
- Allocate time for each section: Before starting, assess the time available and divide it proportionally among the different sections of the test. This ensures that you spend enough time on each question without rushing.
- Start with easier questions: Begin with the questions that you feel most confident about. This will help you build momentum and leave the more difficult questions for later when you have more time to think.
- Keep track of time: Periodically glance at the clock to ensure that you’re staying on schedule. If you’re spending too much time on a single problem, move on and return to it later if needed.
- Don’t overthink questions: If you’re stuck on a question, trust your preparation and make your best guess. Spending too long on one problem can eat into the time you need for others.
- Leave time for review: Set aside the last 5-10 minutes of the test to go back and review your answers. This will give you a chance to catch any mistakes and double-check your work.
By following these strategies, you’ll be able to approach the test with confidence, manage your time efficiently, and maximize your performance on each section.
Common Pitfalls to Avoid

When tackling complex mathematical problems, it’s easy to fall into certain traps that can negatively affect your performance. Recognizing these common mistakes in advance can help you avoid them and improve the accuracy of your responses. Whether it’s overlooking key details or rushing through calculations, staying aware of these pitfalls can make a big difference in your results.
The table below outlines some of the most common mistakes and tips on how to avoid them:
| Mistake | How to Avoid It |
|---|---|
| Skipping Steps | Always show your work, even for simple calculations. This ensures that you don’t miss important details and helps you track your thought process. |
| Misreading the Question | Read each question carefully, paying attention to the specifics. Look for words like “not,” “always,” or “exactly,” which can change the meaning of the problem. |
| Overcomplicating Solutions | Avoid unnecessary steps. Stick to straightforward methods, and remember that simpler approaches are often more effective. |
| Rushing Through Calculations | Take your time to ensure every calculation is correct. If you’re unsure, double-check your work before moving on. |
| Failure to Review | Leave time at the end to go back and review your answers. A fresh perspective often reveals mistakes that were overlooked during the initial pass. |
By staying mindful of these common mistakes, you can approach each problem more methodically and avoid costly errors that can lower your score.
How Scoring Works on AP Calculus AB
Understanding how your performance is evaluated is essential for maximizing your potential score. The scoring system for this type of assessment is designed to reward both accuracy and the process of arriving at solutions. It takes into account not only whether your final answer is correct but also how well you demonstrate your understanding through the steps you take to solve the problems.
The test is typically divided into multiple sections, each with its own set of rules for scoring. Some sections focus on solving problems quickly, while others assess the depth of your reasoning and explanation. Below is an overview of how the scoring generally works:
- Multiple-Choice Questions: Each correct response in the multiple-choice section is awarded one point. There are no penalties for incorrect answers, so it is always beneficial to attempt each question.
- Free-Response Section: This section is scored based on both the correctness of your final answer and the steps you show in your solution. Partial credit is often given for demonstrating the right process, even if the final answer is incorrect.
- Point Distribution: The total score is calculated by combining the points from both sections, with each section contributing a set percentage to the overall score. The free-response section usually accounts for a larger portion of the final score.
- Scoring Scale: After the raw scores are calculated, they are converted to a scale from 1 to 5. A score of 3 or higher is typically considered passing, indicating that you have mastered the key concepts and skills assessed.
Being aware of how your work is scored can help you approach the test strategically. Focus not only on getting the right answers but also on showing your thought process clearly and accurately to maximize your score.
Best Study Resources for AP Calculus AB
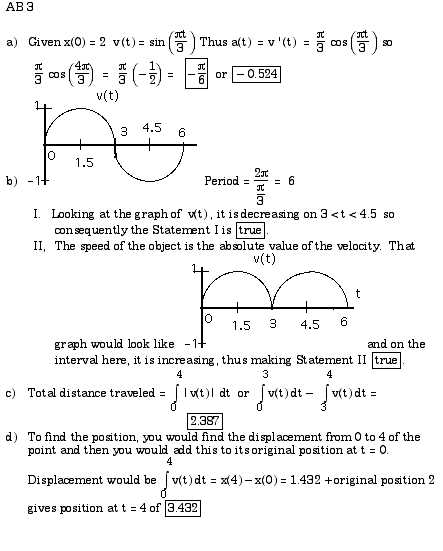
Having the right study materials is key to mastering the concepts and performing well on this type of assessment. There are a variety of resources available that can help you prepare effectively, whether you prefer interactive tools, textbooks, or practice questions. A well-rounded study plan incorporates different types of resources to reinforce your understanding and strengthen your problem-solving skills.
Here are some of the best study resources to help you succeed:
- Textbooks and Review Guides: Comprehensive study guides like Barron’s AP Calculus and Princeton Review’s AP Calculus provide clear explanations of key concepts, along with practice problems and tips for success. These resources offer in-depth coverage of the material and are great for building a strong foundation.
- Online Practice Problems: Websites like Khan Academy and College Board provide interactive exercises and practice questions that closely mirror the content of the test. These platforms offer immediate feedback, which helps you identify areas that need more attention.
- Flashcards: Using flashcards can be a great way to memorize important formulas, theorems, and concepts. You can find pre-made sets on platforms like Quizlet, or create your own to tailor them to your needs.
- Video Tutorials: If you’re a visual learner, video tutorials can be incredibly helpful. Websites like PatrickJMT and Professor Leonard offer step-by-step walkthroughs of problems, explaining complex ideas in simple terms.
- Practice Tests: Taking full-length practice tests under timed conditions is one of the most effective ways to prepare. This helps you get familiar with the format and pacing of the assessment. Many prep books and websites offer full-length practice tests that are designed to simulate the actual test environment.
By utilizing a variety of resources, you can develop a well-rounded understanding of the material and be fully prepared for the challenges you’ll face. Consistent practice and a strategic approach to studying will ultimately help you succeed.
Important Calculus Formulas to Remember
In any advanced mathematical assessment, memorizing and understanding key formulas is essential for success. These formulas form the backbone of solving many types of problems, from finding rates of change to determining areas under curves. Mastery of these formulas not only helps you solve problems more efficiently but also ensures you can handle a wide range of challenges that may appear on the test.
Below are some of the most important formulas to keep in mind:
- Power Rule: If f(x) = x^n, then f'(x) = n * x^(n-1). This rule is fundamental for differentiating polynomial functions.
- Product Rule: If f(x) = g(x) * h(x), then f'(x) = g'(x) * h(x) + g(x) * h'(x). This rule is used when differentiating products of two functions.
- Quotient Rule: If f(x) = g(x) / h(x), then f'(x) = (g'(x) * h(x) – g(x) * h'(x)) / h(x)^2. This helps in differentiating functions that are fractions.
- Chain Rule: If f(x) = g(h(x)), then f'(x) = g'(h(x)) * h'(x). This rule is crucial for differentiating composite functions.
- Area under a Curve (Definite Integral): ∫[a, b] f(x) dx = F(b) – F(a), where F(x) is the antiderivative of f(x). This formula is used to find the area between a curve and the x-axis within a specified interval.
- Fundamental Theorem of Calculus: If F(x) is the antiderivative of f(x), then ∫[a, b] f(x) dx = F(b) – F(a). This connects differentiation and integration, which is vital in solving many problems.
By thoroughly learning and applying these formulas, you’ll be better prepared to solve a variety of problems quickly and accurately. Consistent practice using these formulas is key to success in any advanced math test.
How to Prepare for the Free-Response Section

The free-response section is an essential part of any advanced math assessment, where you are required to solve complex problems and demonstrate your reasoning process. Unlike multiple-choice questions, this section allows you to showcase your understanding by working through each problem step-by-step. Preparing for this section effectively involves practicing problem-solving techniques, improving your time management, and mastering the art of clear, structured solutions.
Here are some strategies to help you prepare for the free-response section:
- Understand the Question Format: The free-response section often includes a mix of theoretical questions, word problems, and application-based problems. Be ready to apply a variety of techniques to solve each one.
- Practice Writing Clear Solutions: Showing your work is crucial for earning partial credit. Practice writing out every step clearly and methodically, even if you can solve the problem mentally. This will ensure that your thought process is evident and can be followed by the grader.
- Time Management: Each question in the free-response section is timed, so it’s important to pace yourself. Allocate a set amount of time for each question, and make sure you leave enough time to review your solutions.
- Work on Common Problem Types: Certain types of questions appear more frequently in this section, such as those related to rates of change, areas under curves, or optimization problems. Practice these types of problems regularly to become more efficient at solving them.
- Review Past Papers: One of the best ways to familiarize yourself with the style and difficulty of free-response questions is by reviewing past assessments. Many practice tests and sample problems are available online and in review books.
By following these strategies and consistently practicing, you will be more confident in your ability to handle the free-response section and perform well. A methodical approach to problem-solving, combined with good time management, will maximize your potential to earn a high score.
AP Calculus AB Practice Tests
Practice tests are one of the most effective ways to prepare for any advanced mathematical assessment. They not only allow you to familiarize yourself with the question format but also help you identify areas that need improvement. By regularly practicing under timed conditions, you can build confidence, enhance your problem-solving skills, and improve your time management. These mock tests simulate the real testing environment, providing you with a realistic preview of what to expect.
Benefits of Practice Tests

Practice tests offer several advantages in your preparation journey:
- Familiarity with Question Types: Practice tests help you understand the types of problems that are commonly asked, allowing you to become more comfortable with them.
- Improving Speed: Timed practice tests help you develop the ability to work efficiently, ensuring you can answer all questions within the given time frame.
- Identifying Weak Areas: By taking practice tests, you can pinpoint areas where you need more focus and practice, which helps optimize your study time.
- Boosting Confidence: Regular practice builds confidence, reducing test-day anxiety and allowing you to approach the real assessment with a calm mindset.
Where to Find Practice Tests
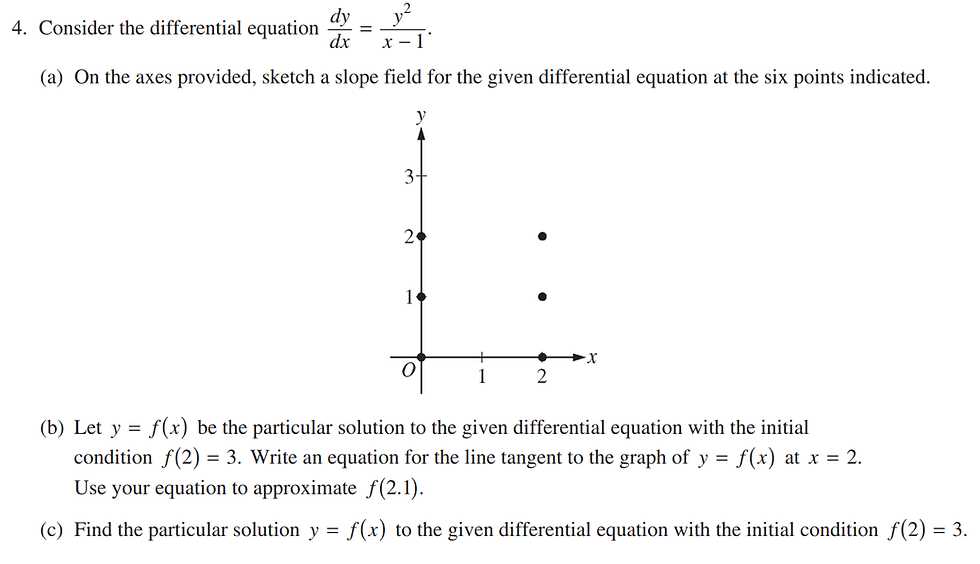
There are many resources available for accessing high-quality practice tests. These can range from official materials published by testing organizations to free resources provided by online platforms. Here are some common places where you can find practice tests:
| Resource | Type of Material | Details |
|---|---|---|
| Official AP Website | Sample Tests | Free practice tests and exam outlines from the official website. |
| Review Books | Practice Tests, Solutions | Books from publishers like Barron’s or Princeton Review that offer practice exams and detailed solutions. |
| Online Platforms | Online Mock Tests | Websites like Khan Academy or College Board provide free or paid access to practice tests. |
Taking practice tests regularly will help ensure that you are fully prepared for the real test, improving your performance and increasing your chances of success.
Understanding Derivatives and Integrals
Derivatives and integrals are two fundamental concepts in advanced mathematics, often working together to describe the relationship between quantities. They are essential tools for analyzing rates of change and areas under curves, helping to model and solve real-world problems. While derivatives focus on the rate at which a quantity changes, integrals calculate the accumulated total or area, providing a powerful way to analyze complex systems.
Grasping the connection between these two ideas is crucial for a deeper understanding of mathematical concepts. Derivatives give insight into how functions behave locally, while integrals provide a broader view of how those behaviors accumulate over a given interval. Together, they offer a complete picture of how quantities interact and change in various contexts.
By mastering these concepts, you can approach a wide range of problems, from calculating speeds and velocities to determining areas and volumes, with greater clarity and precision. Whether you’re analyzing motion, growth patterns, or optimization problems, derivatives and integrals are indispensable tools for mathematical modeling and real-world applications.
Advanced Tips for Problem Solving
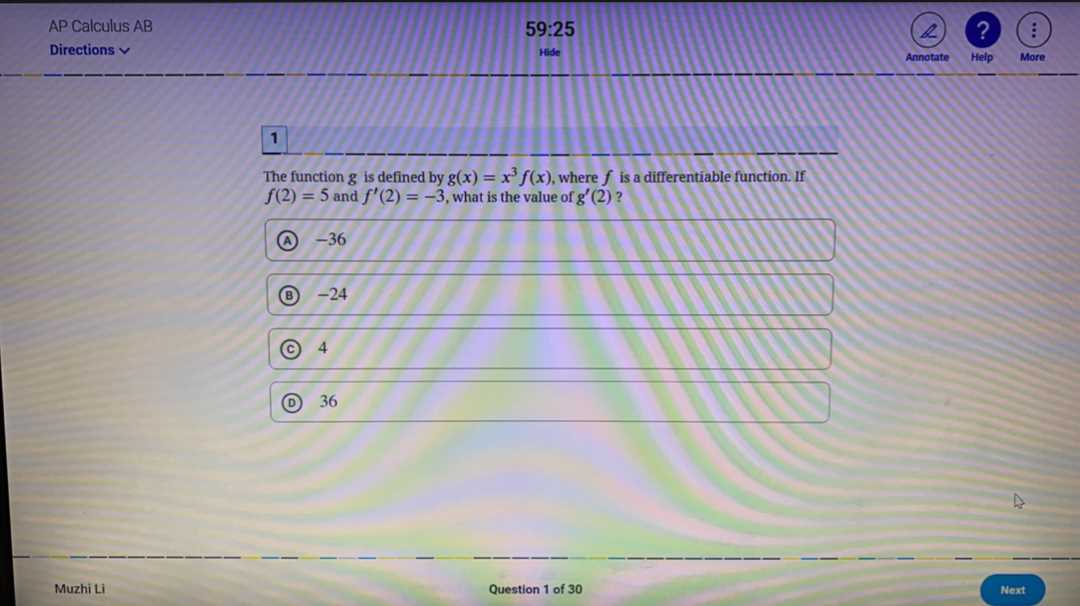
Solving complex mathematical problems requires more than just memorizing formulas or following standard procedures. To approach difficult problems efficiently, it’s important to develop strategic thinking and enhance problem-solving techniques. Whether tackling challenging questions or aiming for faster solutions, employing advanced methods can improve both accuracy and speed.
Break Down the Problem

One of the key strategies for solving tough problems is to break them down into smaller, more manageable parts. Start by identifying the main components of the problem, and consider how each part relates to the others. Simplifying the problem in this way allows you to focus on individual aspects and reduces the chances of getting overwhelmed. Often, solving one smaller piece leads naturally to the solution of the larger problem.
Use Logical Reasoning and Estimation
Another effective approach is to use logical reasoning and estimation to gauge possible solutions. If the exact answer is elusive, try estimating based on known information or using approximate values. This method can help you eliminate clearly incorrect choices in multiple-choice questions and guide you toward the correct solution in free-response scenarios. Logical reasoning can also be used to recognize patterns or relationships that may not be immediately obvious but are crucial for solving the problem efficiently.
By combining these advanced strategies with regular practice, you can enhance your ability to approach even the most complex mathematical challenges with confidence and clarity.
AP Calculus AB Test Day Checklist
The day of the test can be stressful, but having a well-prepared checklist ensures that you are organized and ready to perform your best. By making sure you have all the necessary materials and have reviewed key concepts, you can approach the test with confidence and calm. The checklist below covers everything you need to ensure a smooth test-taking experience.
Start by gathering all the essential tools you’ll need during the test. These items are necessary for answering questions accurately and staying organized throughout the process. Additionally, a solid plan for managing your time during the test can help you stay focused and avoid rushing through questions.
Essential Materials
- Two pencils with erasers
- Approved calculator (check the rules beforehand)
- A valid photo ID
- Comfortable clothing
- Water and snacks for a break (if allowed)
Pre-Test Preparation
- Get a good night’s sleep before the test
- Eat a balanced breakfast
- Arrive at the test center early
- Review key formulas and concepts briefly
- Stay calm and mentally prepared
By following this checklist and staying organized, you can minimize stress and be fully prepared for the challenges ahead. Proper preparation before and on the test day will help you focus on what matters most: performing your best.
How to Handle Test Anxiety
Feeling anxious before or during a test is a common experience, but managing that stress effectively can greatly improve performance. Anxiety can disrupt your focus and make it difficult to recall important information. By understanding the triggers of anxiety and applying certain strategies, you can stay calm and approach the test with confidence.
It’s essential to adopt a proactive mindset. Developing effective stress-management techniques ahead of time can help you stay grounded and perform to your full potential. In this section, we will explore methods that can help you reduce anxiety and maintain focus throughout the test-taking process.
Effective Relaxation Techniques
- Deep breathing exercises: Take slow, deep breaths to help calm your nervous system. Inhale for 4 seconds, hold for 4, and exhale for 4. Repeat this a few times to relax.
- Progressive muscle relaxation: Tense and then relax different muscle groups in your body, starting from your toes and working your way up. This helps release physical tension.
- Visualization: Imagine yourself calmly navigating through the test and succeeding. This positive imagery can reduce anxiety and increase confidence.
Test-Day Mindset
- Prepare early: The more prepared you are, the less anxious you’ll feel. Review key concepts and practice problems regularly leading up to the test.
- Avoid last-minute cramming: Trying to learn new material the night before can increase anxiety. Instead, focus on reviewing and reinforcing what you’ve already studied.
- Stay positive: Replace negative thoughts with positive affirmations. Remind yourself that you’ve prepared and are capable of handling the test.
By implementing these strategies, you can reduce test-related anxiety and approach the situation with a calmer, more focused mindset. Remember, managing stress effectively takes practice, but with the right techniques, you can perform at your best even under pressure.
After the Test: What’s Next?
Once the test is over, it’s time to shift focus to the next steps. The feeling of relief might be immediate, but understanding what happens afterward is important for maintaining momentum. Whether you’re anxiously waiting for results or planning your future steps, the period after a challenging assessment can be a time for reflection and action.
In this section, we will discuss what to do once the test is finished, how to manage your expectations, and what actions you can take while you wait for results. It’s essential to maintain a balanced approach and use the time wisely, whether for further learning or preparation for upcoming challenges.
Reflect on Your Performance
- Review your answers: If allowed, review your test responses to identify areas where you struggled. This self-assessment can help you understand where you need improvement for future tasks.
- Learn from mistakes: Recognizing errors and learning from them will improve your skills and increase your confidence in the long run.
- Seek feedback: Discuss the test with a teacher or a study group to gain valuable insights into your strengths and weaknesses.
Manage Expectations and Results

- Stay patient: Test results often take time, so don’t stress over waiting. Focus on other goals and maintain a positive outlook while awaiting your score.
- Focus on next steps: If the results are as expected, plan for future studies or courses. If they fall short, seek advice on how to improve or retake assessments when necessary.
- Celebrate progress: Regardless of the outcome, celebrate the effort you’ve put in and the progress you’ve made. Growth is just as important as the final result.
After the test, remember that it’s a learning process. Whether you succeeded or faced challenges, there is always room for growth. Use this time to reflect, learn, and prepare for whatever comes next in your academic journey.
How AP Calculus AB Affects College Admissions
Participating in advanced coursework, such as the rigorous assessment in mathematics, can significantly impact your college application process. High school students who take challenging courses like this are often viewed more favorably by admissions committees. By demonstrating strong performance in such subjects, students not only strengthen their academic record but also highlight their ability to handle college-level work.
This section will explore how excelling in these advanced subjects can influence your chances of being accepted into competitive colleges, as well as how it might help in earning college credits or placing out of introductory courses.
How High School Advanced Courses Influence College Applications
- Shows academic readiness: Taking advanced subjects signals to colleges that you are prepared for the demands of higher education. It reflects your intellectual curiosity and your capacity to tackle challenging material.
- Enhances the transcript: A high score in advanced subjects often improves your high school transcript, making you a more competitive applicant, especially at top-tier universities.
- Distinguishes you from other candidates: Many students apply with similar GPA ranges, but those who have pushed themselves with tough coursework stand out.
How Advanced Courses Can Affect College Placement and Credits
- Earn college credits: Many colleges grant credit for high-level coursework, allowing students to bypass introductory courses and advance to more specialized classes sooner.
- Potential for accelerated academic paths: Performing well may even give students the opportunity to place out of foundational classes, thus saving time and tuition fees.
- Impact on scholarship opportunities: Strong performance in difficult subjects can also help qualify students for merit-based scholarships.
In summary, excelling in challenging high school coursework can set you apart in the college admissions process. Not only does it enhance your academic profile, but it can also provide tangible benefits such as college credit or advanced placement, positioning you for success in your higher education journey.