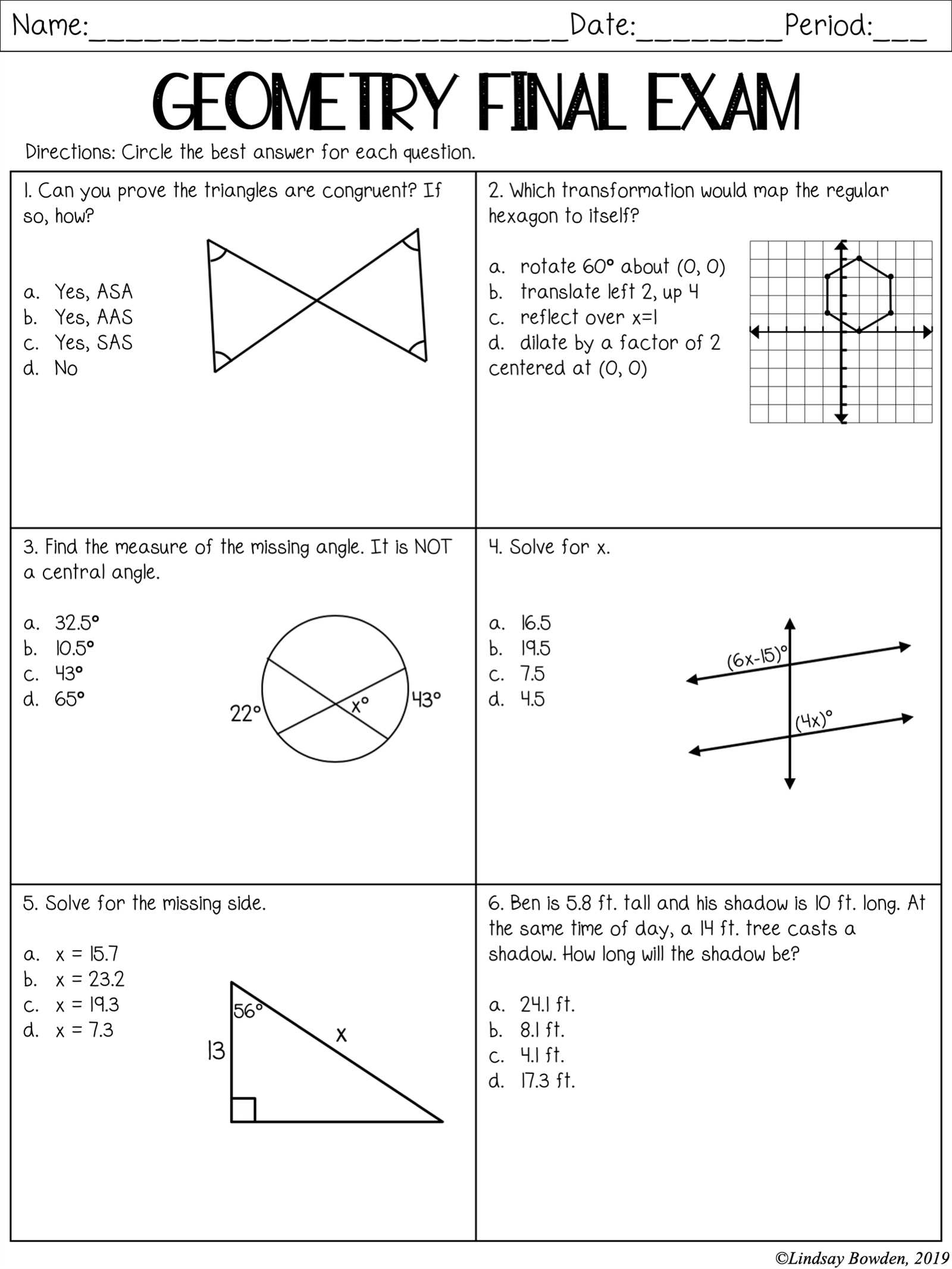
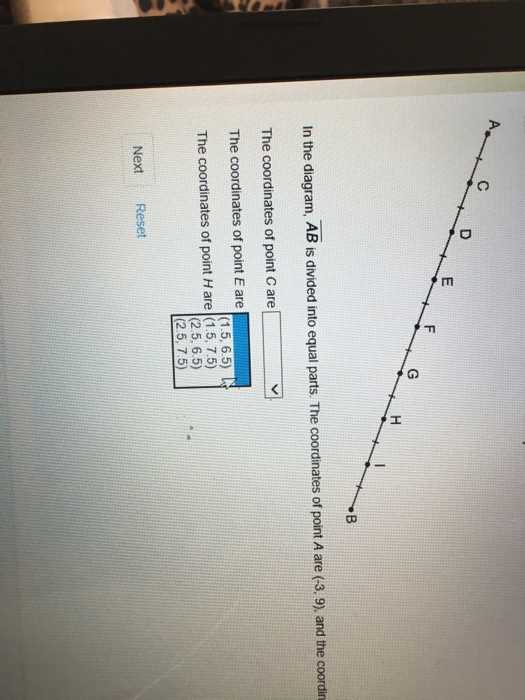
Geometry Semester 2 Final Exam Answer Key

Understanding and mastering the essential concepts covered in advanced mathematical assessments can be challenging. This section is designed to provide clear solutions to the most common questions students face in their academic journey. By reviewing the provided solutions and explanations, you can improve your problem-solving skills and boost your confidence.

Throughout this guide, we will explore various methods for tackling complex mathematical challenges, offering detailed instructions on how to approach each type of problem. Whether it’s mastering formulas or navigating intricate calculations, these resources will help clarify difficult topics and sharpen your analytical abilities.

Emphasis is placed on clarity and precision, ensuring that each step is easy to follow and understand. By familiarizing yourself with these solutions, you will be better equipped to tackle similar problems in future assessments and coursework. With the right tools and strategies, success is within reach.

Mathematical Problem Solutions for Assessment Review

This section offers detailed solutions to a range of questions commonly found in advanced mathematical evaluations. The goal is to provide students with clear guidance, helping them understand the correct methods and techniques for solving complex problems. By reviewing these examples, learners can gain confidence in their abilities and improve their understanding of key topics.

Each problem is broken down into manageable steps, allowing students to follow along and replicate the process on their own. The solutions aim to clarify concepts and demonstrate effective problem-solving strategies that can be applied to similar challenges in the future.

• Step-by-step breakdowns for each problem type
• In-depth explanations of mathematical operations and principles
• Practical tips for approaching difficult questions
• Common mistakes to avoid during problem-solving
• How to verify and double-check your solutions

By carefully studying the provided solutions, students can better grasp the reasoning behind each method, which will help them perform well in future assignments and evaluations. Whether you’re revising or preparing for upcoming challenges, this guide is designed to be a helpful tool on your academic journey.

Overview of Mathematical Assessment for the Term

This section provides a comprehensive look at the evaluation for the end of the term. It is designed to help students understand the scope and structure of the assessment, outlining the key areas that will be tested. By reviewing this, learners can gain clarity on what to expect and focus on the most critical topics for a successful performance.

Topics Covered in the Assessment

The assessment will focus on a range of important concepts, requiring a deep understanding of various mathematical techniques. From working with shapes and figures to solving algebraic expressions, each question is crafted to challenge your knowledge and reasoning skills.

Approach and Strategies for Success

Effective preparation is key to excelling. By familiarizing yourself with the most common types of problems and practicing step-by-step problem-solving methods, you can approach the evaluation with confidence. Reviewing past materials and honing specific skills will help improve your speed and accuracy during the assessment.

Key Concepts Covered in the Term

This section highlights the essential ideas and skills developed throughout the term. The focus is on the core topics that students need to understand thoroughly in order to succeed. By exploring these concepts, learners can reinforce their knowledge and prepare themselves for the challenges ahead.

Understanding Shapes and Their Properties

One of the central themes involves mastering the characteristics of different figures. From triangles to circles, understanding how to calculate dimensions, areas, and volumes is crucial. These skills form the foundation for solving complex problems involving various geometric objects.

Solving Equations and Proofs

Another critical area is the ability to work through logical steps and prove mathematical statements. Whether it’s solving algebraic expressions or proving theorems, mastering this aspect is key to navigating more difficult challenges. Developing a systematic approach to solving problems will improve both efficiency and accuracy.

Common Mathematical Problems in Assessments

During assessments, students frequently encounter a variety of challenges that test their understanding of core concepts. These problems often require a combination of analytical thinking and practical application of formulas. Recognizing the most common types of questions can help students prepare more effectively and develop strategies for solving them with confidence.

Among the most common challenges are those involving calculations related to the properties of different shapes. Problems might include determining areas, perimeters, or volumes, as well as solving for unknown angles in geometric figures. Additionally, students are often asked to apply theorems to prove relationships between elements of figures, which requires logical reasoning and attention to detail.

Another frequent problem type involves working with coordinates and graphs, where students are tasked with finding distances, midpoints, or slopes. These problems combine spatial reasoning with algebraic manipulation, testing both understanding of geometric principles and computational skills. Mastery of these topics is crucial for success in any assessment focused on this subject.

Step-by-Step Solutions for Major Topics

This section provides detailed, step-by-step breakdowns of key problems typically encountered in assessments. Each solution is designed to help students understand the process behind solving complex questions, making it easier to replicate the steps during practice or real challenges. The focus is on clarity and precision, ensuring that each part of the solution is fully explained and easy to follow.

Calculating Areas and Perimeters

One of the most common types of problems involves calculating the area or perimeter of various shapes. Whether dealing with squares, circles, or more complex polygons, students are guided through the specific formulas and how to apply them effectively. By following the steps outlined here, learners will gain the confidence to solve these types of problems accurately.

Proving Theorems and Relationships

Another essential skill is the ability to prove mathematical statements or relationships between different elements in a figure. The process involves logical reasoning, using known properties and theorems to establish new facts. This section explains how to approach these problems systematically, ensuring that each step is backed by solid reasoning.

Understanding Mathematical Formulas and Theorems

To succeed in solving complex problems, it’s essential to have a strong grasp of the fundamental formulas and theorems used to determine unknown values and relationships. This section explores key mathematical concepts, providing the tools necessary for solving a wide range of problems. Whether it’s finding the area of a figure or proving relationships between angles, understanding these formulas is critical for success.

Common Formulas for Area and Volume

Mathematical formulas for calculating the area and volume of different shapes are essential tools in problem-solving. Each formula is derived based on the properties of the shape, and learning how to apply them correctly is crucial for accuracy. Below is a table of commonly used formulas:

Shape	Formula	Description
Square	Area = side²	Calculates the area by squaring the length of one side.
Rectangle	Area = length × width	Determines the area by multiplying length and width.
Circle	Area = π × radius²	Finds the area by squaring the radius and multiplying by π.
Triangle	Area = ½ × base × height	Uses half the base times the height to calculate area.
Sphere	Volume = 4/3 × π × radius³	Calculates the volume by using the cube of the radius.

Key Theorems in Mathematical Problem Solving

Theorems form the foundation for proving relationships between different elements. Understanding the application of these principles can simplify complex problems and lead to logical solutions. Some key theorems include the Pythagorean theorem, properties of parallel lines, and angle relationships in polygons.

Tips for Solving Complex Mathematical Questions

When faced with challenging problems, having a strategy can make a significant difference in your approach and outcome. This section provides practical tips for tackling difficult questions, helping you break down complex tasks into manageable steps. By following these strategies, you can enhance your problem-solving abilities and improve your efficiency during assessments.

• Understand the Problem Thoroughly: Before jumping into calculations, take time to read the problem carefully and identify the key elements involved. Recognizing what is given and what needs to be found is crucial for effective problem-solving.
• Draw Diagrams: Visualizing the problem can help you understand the relationships between different parts. Create diagrams or sketches to clarify the scenario and assist in identifying the correct approach.
• Break the Problem into Smaller Parts: Large problems can seem overwhelming, but breaking them down into smaller, simpler parts makes them more manageable. Solve each part step by step to avoid errors and confusion.
• Apply Relevant Formulas: Ensure that you are using the correct formulas for the problem at hand. Always check that the formula matches the type of figure or relationship described in the question.
• Check for Patterns or Symmetry: Many problems involve repetitive patterns or symmetrical properties. Identifying these can simplify the solution process and save time.
• Double-Check Your Work: After solving, go over your steps to ensure there are no mistakes. Verifying your calculations and reasoning helps to confirm the accuracy of your solution.

By implementing these strategies, you’ll be better equipped to approach and solve even the most difficult problems, turning complex challenges into opportunities to showcase your skills and understanding.

Common Mistakes to Avoid in Assessments

When working through problems in assessments, it’s easy to make mistakes, especially under time pressure. Being aware of the most frequent errors can help students avoid common pitfalls and improve their performance. This section highlights some of the mistakes to watch out for and offers tips for preventing them.

Mistake	Description	How to Avoid It
Forgetting to label figures	Often, students forget to mark important points, lines, or angles in diagrams, which can lead to confusion.	Always label key elements in the figure to ensure clarity and avoid missing critical information.
Incorrect use of formulas	Using the wrong formula for a given shape or problem is a common error, especially when under pressure.	Double-check the formula before applying it, and ensure it matches the problem’s requirements.
Skipping steps	Rushing through problems can result in skipping essential steps, leading to incomplete or incorrect answers.	Take your time and solve problems methodically, writing out each step clearly.
Misinterpreting the question	Sometimes students misread the question, leading to a misunderstanding of what is being asked.	Carefully read the problem multiple times and highlight key information before starting your solution.
Not checking work	Failing to review calculations and reasoning often leads to avoidable mistakes in the final answer.	Always review your work to catch errors in calculations or logic before submitting your response.

By staying mindful of these common mistakes, students can approach problems more confidently and ensure they apply their knowledge accurately. Taking the time to carefully check each step and avoid hasty assumptions will lead to better results and improved performance on assessments.

Mathematical Problem-Solving Techniques

Solving complex mathematical problems requires a combination of strategy, knowledge, and critical thinking. Understanding and applying the right problem-solving techniques can significantly improve the ability to tackle a wide range of challenges. This section explores some of the most effective methods to approach difficult questions, making them more manageable and ensuring accurate results.

Logical Step-by-Step Approach

One of the most important techniques is to break down a problem into smaller, more manageable parts. Start by identifying what is known and what needs to be determined. Then, proceed step by step, using logical reasoning to move from one part of the problem to the next. This method helps ensure no critical elements are overlooked and minimizes the risk of errors.

Utilizing Visual Aids

Drawing diagrams or creating charts can simplify complex problems by providing a visual representation of the relationships between different elements. By organizing the given data visually, it’s easier to spot patterns, identify missing information, and develop a clearer understanding of the problem. This technique is particularly useful in spatial or measurement-based problems.

How to Use the Solution Guide Effectively

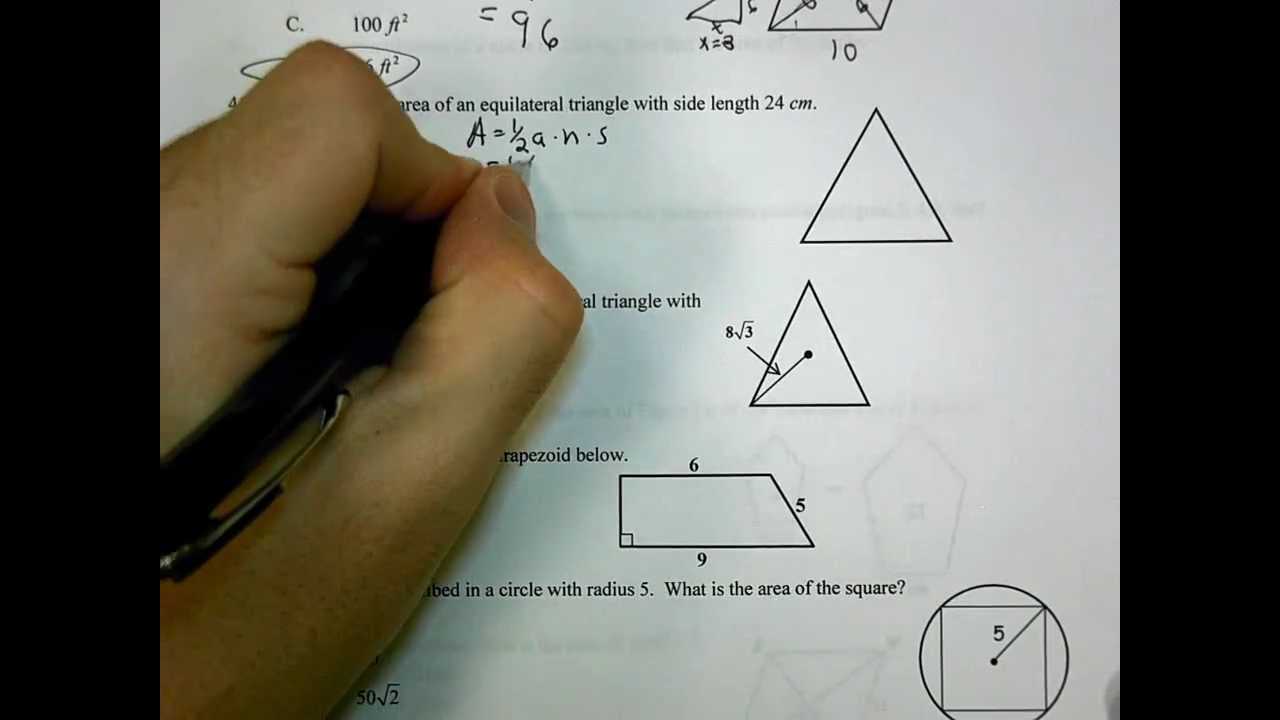
Having access to a solution guide can be incredibly helpful for reinforcing concepts and verifying results. However, it’s important to use it in a way that supports learning rather than just providing quick fixes. This section outlines how to make the most of a solution guide to enhance your understanding and improve your problem-solving skills.

Review Solutions After Attempting Problems

It’s tempting to check the solution guide right away, but it’s more beneficial to try solving the problems on your own first. Once you’ve made your attempt, compare your solution with the provided answers. This process will help you identify areas where you went wrong and give you insight into the correct approach.

• Compare your steps with those in the solution guide.
• Focus on understanding the reasoning behind each step, not just the final result.
• Identify any mistakes in your approach and learn from them.

Use the Guide to Clarify Concepts

The solution guide is not only for checking your answers but also for deepening your understanding of the concepts. When you encounter a problem that you struggled with, refer to the guide to see the methodology used. Take note of any new techniques or formulas introduced, and try to apply them to similar problems to strengthen your grasp of the topic.

• Pay attention to patterns in how solutions are structured.
• Revisit any formulas or theorems you didn’t fully understand during your initial attempt.
• Use the guide as a resource to reinforce your conceptual knowledge.

By approaching the solution guide as a learning tool rather than just a shortcut, you’ll not only improve your performance but also build a stronger foundation for future challenges.

Reviewing Key Mathematical Terms and Definitions

Understanding the fundamental terminology is crucial when tackling mathematical problems. Mastery of essential concepts, definitions, and terms ensures clarity when solving problems and helps build a solid foundation for more complex challenges. In this section, we will revisit some of the most important terms to solidify your grasp of key ideas and improve your problem-solving abilities.

Key terms like angles, shapes, and equations form the building blocks of many problems. These terms often define how you approach a question and influence the steps you take to find the solution. Becoming familiar with their meanings and applications will lead to a better understanding of the problem-solving process.

• Angle: The space between two intersecting lines, measured in degrees or radians.
• Perimeter: The total distance around a shape, calculated by adding the lengths of its sides.
• Area: The measure of the surface enclosed within a shape, typically expressed in square units.
• Congruence: When two shapes have the same size and shape, although they may be oriented differently.
• Similarity: When two shapes have the same shape but may differ in size.

By continuously reviewing and reinforcing these key terms, you’ll be better equipped to handle problems and apply the correct formulas or strategies as needed. Knowing the definitions and how they relate to each other is fundamental for both basic and advanced problem-solving.

How Mathematical Questions Are Graded

Understanding how mathematical problems are graded is essential for knowing what to focus on during preparation. Grading often goes beyond just providing the correct result; it involves evaluating the entire process, from the initial steps to the final solution. In this section, we will explore the general grading criteria and what instructors typically look for when assessing responses.

Typically, grading involves evaluating both accuracy and the methodology used to solve the problem. While the final result is important, the steps taken to reach that solution demonstrate the depth of understanding. A strong response not only shows the correct answer but also includes a clear and logical process that can be followed and understood by others.

• Clarity of Steps: It’s crucial that the steps taken to solve the problem are well-organized and easy to follow. Even if the final result is correct, unclear or missing steps can lead to partial credit deductions.
• Correct Application of Formulas: The use of appropriate formulas and the correct substitution of values is critical. Mistakes in applying formulas often lead to significant point reductions.
• Logical Reasoning: Demonstrating clear reasoning and justifying each step is important. Instructors look for evidence that the student understands why certain operations are performed and how they contribute to the solution.
• Final Answer: The accuracy of the final answer is essential. However, even when the answer is correct, instructors may award partial points for the process if the steps are logically sound.

By keeping these grading criteria in mind, you can improve your ability to perform well on assessments and ensure that your work demonstrates both thorough understanding and accuracy. Grading focuses not only on the destination but also on the journey you take to reach the solution.

Time Management During the Assessment

Effectively managing your time during a high-stakes evaluation is crucial for maximizing performance. Proper time allocation allows you to approach each problem with focus and ensures that you can complete all tasks within the allotted time. In this section, we will discuss strategies for managing time efficiently, helping you avoid rushing through questions and maximize the quality of your responses.

Strategies for Efficient Time Allocation

To ensure that you make the most of your time, it is essential to break the assessment into manageable parts. Here are some tips for managing your time effectively:

• Read Through the Entire Paper: Before starting, quickly review all the questions to get a sense of their difficulty and allocate time accordingly. This will help you identify easier questions to solve first and more challenging ones later.
• Time Allocation per Question: Set a specific time limit for each question based on its complexity. Stick to these limits and move on if you find yourself spending too much time on a single question.
• Prioritize Easier Questions: Tackle the questions you find easiest first. This will give you a sense of accomplishment and leave more time for tougher problems.
• Leave Time for Review: Make sure to reserve some time at the end to review your answers. This is especially important for catching mistakes or recalculating answers to verify accuracy.

Avoiding Common Time Traps

There are common time-wasting behaviors that can easily hinder your performance if you aren’t careful. Be mindful of the following:

• Overthinking: Don’t overcomplicate simple questions. If you’re unsure, move on and come back later with fresh eyes.
• Skipping Steps: It may be tempting to skip certain steps in the problem-solving process, but this can lead to mistakes. Stay consistent in showing your work to avoid unnecessary errors.
• Rushing at the End: In the final moments, don’t rush to finish. Carefully check your work, especially for errors that may have been overlooked during the initial pass.

By following these time management strategies, you can approach each question confidently and ensure that you complete the assessment to the best of your ability.

Preparing for the Assessment with Practice

One of the most effective ways to prepare for a rigorous test is through consistent practice. By engaging with a variety of problems and applying learned concepts, you can strengthen your understanding and increase confidence. In this section, we will explore the benefits of practice, different approaches to practicing, and how to incorporate it into your study routine for optimal results.

Why Practice Matters

Practice plays a crucial role in reinforcing knowledge and improving problem-solving skills. It helps you become familiar with the types of questions you may encounter, reduces anxiety, and enhances your ability to apply the concepts in real-world situations. Consistent repetition allows you to identify patterns and develop strategies for approaching different kinds of challenges.

• Reinforces Learning: Repetition strengthens the neural pathways associated with each concept, making it easier to recall when needed.
• Boosts Confidence: As you solve more problems, you build the confidence needed to tackle even the most challenging questions.
• Improves Time Management: Regular practice helps you become familiar with the time constraints and learn how to allocate time efficiently.

Effective Practice Techniques

To get the most out of your practice sessions, focus on variety and gradual progression. Here are a few techniques to help structure your practice:

• Work on Sample Problems: Practice with a wide range of sample questions to cover all potential topics. This allows you to identify areas of weakness and focus your efforts on improving them.
• Use Past Assessments: If available, review previous assessments or practice tests. These offer a realistic idea of the types of questions to expect and the format of the test.
• Set Timed Sessions: Mimic actual testing conditions by timing yourself. This helps build the ability to solve problems under pressure.
• Review Solutions: After attempting a problem, review the correct solution to understand where you made errors and how to improve your approach.

Tracking Progress

As you continue to practice, it’s essential to monitor your progress and adapt your study plan accordingly. Here’s a table that can help you track your improvement:

Topic	Initial Score	Current Score	Next Steps
Basic Equations	65%	85%	Continue practicing, focus on complex problems
Shapes and Properties	70%	90%	Review theory and apply to more problems
Proofs and Theorems	50%	75%	Study definitions and solve related exercises

By tracking your performance and adapting your study sessions, you can maximize the effectiveness of your preparation and approach the assessment with confidence.

How to Check Your Responses Accurately

Reviewing your work carefully is an essential step in ensuring accuracy and avoiding simple mistakes. By adopting effective strategies, you can verify your solutions methodically and increase the likelihood of identifying errors before submitting your work. In this section, we’ll explore different techniques to double-check your results and ensure everything is correct.

The first step is to take your time and avoid rushing through the verification process. Even if you’re confident in your solutions, it’s important to step back and examine each step of your work. Look for common issues like calculation mistakes, overlooked details, or missed steps in the logic. To make the review process smoother, break your tasks into smaller sections and focus on one aspect at a time.

• Verify Calculations: Go through your computations carefully. Check each arithmetic operation, as small errors can lead to incorrect results.
• Check Consistency: Ensure that all parts of your work align logically. For example, if you’re solving a multi-step problem, confirm that each solution step is consistent with the previous one.
• Use Different Methods: If possible, try solving the same problem in an alternative way. Comparing different approaches can help verify the correctness of your solution.
• Work Backwards: In some cases, working backward from your final answer can help identify discrepancies or logical flaws in your reasoning.

Additionally, take advantage of available resources to cross-check your work. Refer to example solutions, guidelines, or textbooks to ensure that your answers meet expected standards. It’s also helpful to ask someone else, like a peer or instructor, to review your solutions. A fresh perspective often catches mistakes that you may have overlooked.

By following these tips, you can ensure that your responses are not only accurate but also carefully considered, boosting your overall performance and confidence in your abilities.

Final Assessment Tips for Students

Preparing for a comprehensive evaluation requires strategic planning and effective study methods. Whether you’re facing a written test or problem-solving challenges, having a clear approach can significantly enhance your chances of success. In this section, we provide valuable tips to help students perform at their best during the assessment period.

First and foremost, ensure that you fully understand the scope of the material. Review your notes, assignments, and any practice exercises that were completed during the course. Identifying key topics and revisiting any areas where you struggled will help reinforce important concepts. Time management is also essential–organize your study sessions so you can focus on one topic at a time without feeling overwhelmed.

Tip	Action
Prioritize Key Topics	Identify the main concepts likely to appear and focus your study on these areas.
Practice with Past Materials	Work through previous assignments, practice problems, and sample questions to familiarize yourself with the format.
Take Breaks	Give yourself time to rest between study sessions to avoid burnout and retain information better.
Review Mistakes	Go over errors from past assignments or tests to understand what went wrong and how to correct it.
Stay Organized	Keep your study space and materials organized for easy access to notes, tools, and resources.

Additionally, practice problem-solving under time constraints to improve your ability to think critically and respond quickly during the actual assessment. This approach helps to build confidence and reduce anxiety. If you encounter any challenging topics, don’t hesitate to seek assistance from classmates, instructors, or online resources.

By following these effective strategies, you can maximize your chances of performing well and showcasing your understanding of the material. Success in your upcoming evaluation will be a result of smart preparation, focus, and persistence.

Additional Resources for Students

In addition to regular study sessions and practice problems, there are many other tools available to help you deepen your understanding and improve your performance. Whether you’re seeking additional explanations, practice materials, or interactive learning experiences, these resources can offer valuable support. Below are several options that students can explore to enhance their study routines and boost their learning process.

Online Platforms

There are many websites dedicated to providing tutorials, practice exercises, and interactive learning experiences. These platforms often include step-by-step guides and video explanations that can make complex concepts easier to understand.

• Khan Academy: Free educational videos and exercises covering various topics, including mathematical reasoning and problem-solving strategies.
• Wolfram Alpha: A computational search engine that can help solve equations and visualize concepts.
• Coursera: Offers courses from universities around the world, many of which provide deeper insights into problem-solving and theoretical concepts.
• Brilliant.org: Interactive learning platform with courses focused on critical thinking and problem-solving skills in various fields, including mathematics.

Books and Study Guides

Books can provide a more comprehensive approach to the material, with detailed explanations and worked-out examples. Some popular titles include:

• “The Art of Problem Solving” by Richard Rusczyk: An excellent resource for students looking to improve their problem-solving techniques and mathematical reasoning.
• “Precalculus: Mathematics for Calculus” by James Stewart: Offers a thorough review of mathematical principles, ideal for students preparing for higher-level studies.
• “The Humongous Book of Basic Mathematics” by W. Michael Kelley: A great study guide for strengthening foundational skills in various mathematical areas.

These additional resources offer students a range of options to expand their learning. By utilizing a combination of online tools, textbooks, and guided practice, you can reinforce the concepts covered in class and gain a deeper understanding of the material. Keep in mind that the best resources are those that align with your learning style and specific areas of need.