Geometry Regents Exam Questions and Answers by Topic

Success in high school mathematics assessments requires a strategic approach that aligns with the specific curriculum and essential concepts. Understanding how to navigate the various problems presented, and honing skills in applying mathematical principles, is crucial for achieving strong results. The key to performing well lies in consistent practice, reviewing the right material, and mastering the methods that frequently appear on these evaluations.

In this section, we will explore a structured way to tackle the challenges that often arise in the mathematical assessments required for graduation. By breaking down the material into manageable sections, students can focus on areas that need improvement while reinforcing their strengths. This methodical review ensures a deeper understanding of the subject matter, helping learners to approach problems with confidence.

Preparation involves not only knowing the formulas and techniques but also practicing how to apply them under timed conditions. With the right resources and focused effort, you can gain the skills necessary to approach each problem efficiently and accurately.

Geometry Regents Exam Preparation Tips

Proper preparation is key to mastering any assessment. By organizing your study plan and focusing on the most important aspects of the material, you can boost your confidence and improve your performance. A structured approach to learning helps identify weak areas, allowing for targeted review and practice.

Here are some essential tips to guide your preparation:

• Familiarize Yourself with the Format: Understand the types of problems you will encounter and the format of the evaluation. Knowing the structure will help you feel more comfortable on the day of the test.
• Practice Regularly: Consistent practice with sample problems is crucial. The more problems you solve, the more familiar you become with the question styles and techniques needed to solve them.
• Master Key Concepts: Focus on fundamental principles such as shapes, measurements, and transformations. These concepts form the backbone of many problems and mastering them will make solving others easier.
• Use Timed Practice Sessions: Simulate test conditions by timing yourself while solving problems. This helps you manage your time effectively during the actual test.
• Review Mistakes: Analyze the problems you got wrong and understand why you made those mistakes. This helps you avoid repeating them in the future.

By following these strategies and staying focused on the key areas, you’ll be well-prepared to approach any problem with confidence and accuracy.

Overview of Geometry Regents Exam Structure

Understanding the structure of the assessment is an essential step in preparing effectively. The format of the test is designed to evaluate a student’s ability to apply various mathematical concepts in problem-solving situations. This section will break down the key components, providing insight into how the test is organized and what you can expect during each part.

Sections of the Test

The assessment is divided into several sections, each focusing on different areas of mathematical understanding. These sections test a variety of skills, ranging from basic principles to more complex problem-solving strategies. Each part is carefully constructed to ensure that students demonstrate both conceptual knowledge and practical application of techniques.

Time Allocation and Scoring

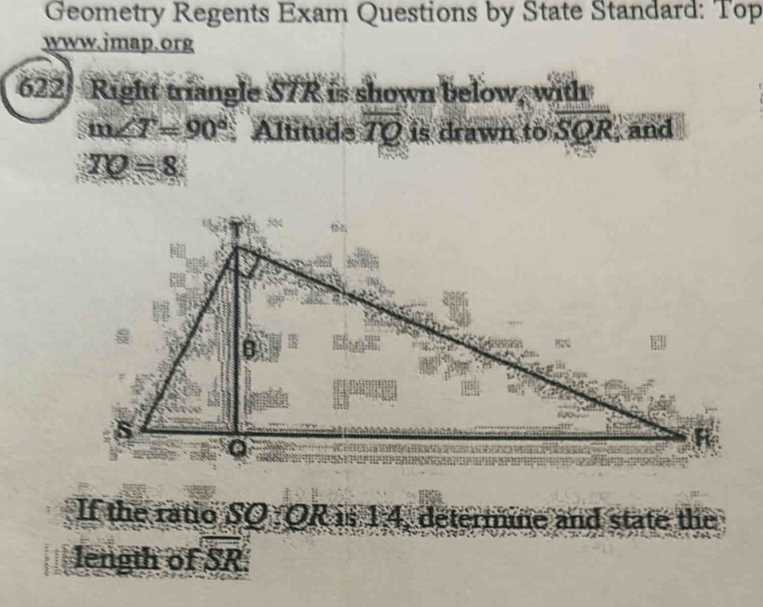
Time management is an important aspect of the assessment. The test is structured to be completed within a set timeframe, with each section allotted a specific duration. Understanding how to allocate your time across different sections is crucial to completing the test successfully. Scoring is based on the accuracy and thoroughness of your solutions, and partial credit may be awarded for correct reasoning, even if the final answer is not fully accurate.

Key Topics Covered in Geometry Exams

In order to succeed on the assessment, it’s essential to have a strong grasp of the core mathematical concepts that are commonly tested. These topics cover a broad range of principles and problem-solving techniques that are integral to understanding shapes, their properties, and how they interact within various systems. Mastery of these areas will provide a solid foundation for tackling the challenges on the test.

Core Mathematical Concepts

The areas covered include a mix of fundamental and advanced topics, each contributing to your overall understanding. These concepts range from basic geometric properties to more complex applications such as transformations and spatial reasoning. Below is a breakdown of some of the most important themes to focus on:

Topic	Description
Angles and Triangles	Understanding the relationships between angles, side lengths, and triangle properties.
Circles	Properties of circles, including radius, diameter, and circumferences, as well as related theorems.
Transformations	Exploring the effects of translations, rotations, reflections, and dilations on geometric figures.
Coordinate Geometry	Using the coordinate plane to solve problems involving distance, midpoints, and slopes.
Solid Figures	Understanding three-dimensional shapes and calculating volume and surface area.

Problem-Solving Techniques

In addition to conceptual understanding, it is important to practice applying these concepts in a variety of problem-solving scenarios. Developing strategies for recognizing patterns and making logical deductions is critical for solving more complex challenges during the test. Familiarity with these key areas will allow you to approach problems with confidence and precision.

How to Approach Geometry Questions

When faced with a set of mathematical problems, a systematic approach is essential for solving them efficiently and accurately. By breaking down each problem into manageable steps, you can increase your chances of success. Understanding how to interpret the given information and applying the right strategies will allow you to navigate through the challenges effectively.

Step-by-Step Problem Solving

Before attempting to solve any problem, take a moment to understand what is being asked and identify the key elements. Here’s a recommended approach to tackling each problem:

• Read Carefully: Make sure you understand all the given details before starting. Look for known values, unknowns, and any relationships between them.
• Draw Diagrams: If the problem involves shapes or figures, drawing a diagram can help you visualize the situation and clarify the relationships between different elements.
• Identify Key Concepts: Determine which mathematical principles or formulas apply to the problem at hand. These could be related to angles, lengths, areas, or transformations.
• Work Step by Step: Break the problem into smaller, more manageable steps. Solve one part at a time, rather than trying to tackle the entire problem at once.
• Check Your Work: After reaching a solution, review the steps and the final answer to ensure accuracy. Make sure it makes sense in the context of the problem.

Handling Complex Problems

Some problems may appear difficult at first glance, but with the right approach, they can be simplified. If a problem seems complicated, try the following:

1. Look for Patterns: Identify recurring elements or relationships that may simplify the problem.
2. Use Approximations: If exact calculations are difficult, estimate values to get a rough idea of the solution.
3. Break the Problem into Sub-Problems: If the problem involves multiple parts, tackle each one individually before combining them for the final solution.
4. Stay Organized: Keep track of your work and maintain clarity in your reasoning. This will help avoid mistakes and keep the process on track.

Understanding State Standards for Geometry

Familiarizing yourself with the expectations set for academic proficiency in mathematics is crucial for successful preparation. These guidelines outline the specific knowledge and skills that students should master by the time they complete their studies. By understanding the key areas that are regularly tested, you can focus your efforts on mastering the necessary material.

Core Concepts and Skills

The guidelines highlight essential mathematical concepts that form the foundation for problem-solving. These concepts are designed to ensure students can demonstrate their ability to apply mathematical reasoning and techniques in real-world contexts. Key areas include:

• Spatial Understanding: Recognizing and manipulating shapes, understanding their properties, and applying this knowledge to solve problems.
• Measurement and Calculation: Accurate measurement of lengths, areas, and volumes, as well as using formulas to calculate different properties of figures.
• Logical Reasoning: The ability to make deductions, justify steps, and use logical sequences to solve problems effectively.
• Problem-Solving Strategies: Developing a systematic approach to addressing mathematical challenges and applying appropriate techniques.

Application of Skills

In addition to theoretical knowledge, it is important to be able to apply the learned skills to various types of problems. The guidelines emphasize the importance of understanding how these principles can be used to solve practical and abstract problems. This ensures that students not only know the material but can also demonstrate their understanding in varied situations.

Essential Formulas for Geometry Regents

Mastering key mathematical formulas is a fundamental part of succeeding in any assessment that involves spatial reasoning and problem-solving. These formulas serve as the tools needed to solve various types of problems involving shapes, distances, and other geometric relationships. By becoming familiar with these essential equations, you can approach challenges with confidence and precision.

Basic Formulas

Below are some of the most important formulas that you should memorize and understand. These equations are frequently used in various problems and are critical for solving geometry-related tasks.

Formula	Application
Area of a Rectangle	Length × Width
Area of a Triangle	1/2 × Base × Height
Area of a Circle	π × Radius²
Circumference of a Circle	2 × π × Radius
Pythagorean Theorem	a² + b² = c² (for right triangles)
Surface Area of a Rectangular Prism	2lw + 2lh + 2wh

Advanced Formulas

For more complex problems, you will also need to know advanced formulas that involve three-dimensional shapes and other mathematical relationships. These formulas help calculate volumes, surface areas, and other measurements in more intricate scenarios.

Formula	Application
Volume of a Cylinder	π × Radius² × Height
Volume of a Cone	1/3 × π × Radius² × Height
Volume of a Sphere	4/3 × π × Radius³

By practicing these formulas and understanding when to apply each one, you’ll be better equipped to solve the mathematical challenges presented during the assessment.

Top Strategies for Solving Geometry Problems

Successfully solving mathematical problems requires a combination of logical thinking, familiarity with key concepts, and efficient problem-solving techniques. To enhance your ability to tackle challenges, it’s important to adopt strategies that can help you systematically approach and resolve each problem. Developing these methods can significantly improve your problem-solving speed and accuracy.

Step-by-Step Approach

One of the most effective methods for solving any problem is to break it down into smaller, manageable steps. Here are a few strategies to consider:

• Understand the Problem: Carefully read the problem to ensure you understand all the details and what is being asked. Look for any hidden information or relationships between elements.
• Draw Diagrams: Visual representation of the problem can simplify complex situations, especially when dealing with shapes and distances. Sketching helps you visualize the problem and organize your thoughts.
• Identify Key Relationships: Recognize the mathematical relationships at play, such as symmetry, congruence, or proportionality. This can guide you to the right approach for solving the problem.
• Apply Relevant Formulas: Use known equations or theorems that relate to the shapes and values in the problem. Ensure you know which formulas to apply in different scenarios.
• Check Your Work: After solving, review the steps and results to confirm that they make sense. This ensures accuracy and helps catch any mistakes made during the process.

Handling Complex Problems

For more complicated problems, it’s essential to stay organized and patient. Here are additional strategies to help you manage difficult challenges:

• Look for Patterns: In more complex problems, identifying repeating elements or patterns can simplify the solution process. These patterns often point to shortcuts or faster methods for solving.
• Work Backwards: In some cases, starting from the desired outcome and working backwards can reveal the necessary steps to reach the solution. This approach helps in reverse engineering the problem.
• Use Approximation: If exact calculations are difficult, consider estimating values to narrow down the possibilities. This can guide you towards the correct answer when the problem becomes overwhelming.

Common Mistakes to Avoid in Geometry

While solving mathematical problems, it’s easy to make simple mistakes that can derail your solution. Recognizing common errors is an important step in improving your problem-solving skills. By being aware of these pitfalls, you can prevent them and ensure more accurate and effective results.

Careless Calculation Errors

One of the most frequent mistakes students make is failing to perform basic calculations correctly. Here are some common errors to watch out for:

• Sign Errors: Neglecting to account for negative signs when adding or subtracting can lead to incorrect results.
• Misapplying Formulas: Sometimes, students confuse or misuse formulas, applying them in the wrong context or leaving out essential components, which leads to errors.
• Incorrect Units: Forgetting to include proper units when working with measurements can result in a solution that doesn’t make sense.
• Arithmetic Mistakes: Simple addition, subtraction, multiplication, or division errors are often made under time pressure, but they can dramatically affect the outcome of your problem-solving process.

Conceptual Misunderstandings

Understanding the underlying principles of the subject is key to solving problems effectively. Some errors stem from a lack of grasp of basic concepts:

• Ignoring Relationships Between Elements: Failing to recognize how different shapes or parts of a problem are connected can cause confusion and lead to incorrect conclusions.
• Misunderstanding Symmetry and Proportions: Problems that involve symmetry or proportions require careful attention to detail. Many students make mistakes when interpreting these properties.
• Forgetting Theorems or Postulates: Certain problems rely on specific theorems or postulates (like the Pythagorean theorem or the properties of parallel lines). Forgetting these can lead to unnecessary confusion or missed opportunities to apply shortcuts.

Poor Time Management

Time pressure can sometimes cause students to rush through problems, which increases the likelihood of mistakes. Here are a few ways poor time management can lead to errors:

• Rushing Through Steps: When you’re pressed for time, it can be tempting to skip steps or overlook important details. This often leads to incomplete or incorrect solutions.
• Neglecting to Double-Check Work: Not reviewing your calculations or reasoning can allow small errors to slip through. Taking a moment to check your work at the end of each problem can save you from simple but costly mistakes.

Time Management During the Exam

Effective time management is crucial when working under pressure. Whether you’re tackling complex problems or multiple-choice questions, knowing how to allocate your time wisely can make a significant difference in your performance. By prioritizing tasks and staying organized, you can maximize your chances of success.

The key to mastering time management is to stay focused and avoid getting stuck on a single problem. It’s important to pace yourself and not dwell too long on any one question, as this can lead to missed opportunities and unnecessary stress. Here are some strategies to help manage your time efficiently during a timed assessment.

Prioritize the Easier Problems

Start by tackling the questions that are easiest for you. These typically take less time and can help build confidence early on. Once you have completed the simpler problems, you’ll have more time and mental energy for the more challenging ones. This approach can also ensure that you don’t leave any questions unanswered.

• Scan the Entire Paper: Quickly review the full set of problems to get an idea of the time needed for each one.
• Identify Low-Effort Questions: Pick the ones that require less time to solve and work on them first.
• Avoid Perfectionism: Don’t waste too much time trying to achieve perfect solutions on easier problems.

Set Time Limits for Each Section

Breaking the assessment into sections and setting time limits for each one can help keep you on track. This prevents you from spending too much time on any one section and ensures that all areas are covered within the allotted time. Use a watch or clock to stay mindful of your progress and adjust your pace if necessary.

• Use a Timer: Set a timer for each section of the assessment to help you stay on schedule.
• Move On When Stuck: If you encounter a problem that seems difficult, move on to the next one and come back to it later if time allows.
• Be Mindful of Remaining Time: Regularly check the time to make sure you’re keeping pace and haven’t fallen behind.

Leave Time for Review

Reserving some time at the end for a final review is essential. During this time, check your work for any simple mistakes or overlooked details. Having a few minutes to revise your answers can help you catch errors that may have been missed during the initial solving process.

• Check for Calculation Mistakes: Quickly review your calculations to ensure there are no simple arithmetic errors.
• Ensure Completeness: Verify that all parts of each question are answered fully.
• Review Complex Problems: If time allows, return to the more challenging problems to check your reasoning and solution.

Reviewing Practice Questions by Topic

Focusing your review on specific areas of study is an effective strategy for mastering material. By organizing your preparation around key concepts, you can identify areas of strength and target areas that need improvement. Breaking down your practice into distinct sections helps reinforce your understanding and boosts confidence before taking on more complex challenges.

Rather than simply reviewing all material in a random order, it’s important to focus on particular themes or concepts. This approach allows you to address any weak spots while reinforcing knowledge in stronger areas. Reviewing systematically also helps with retention, as it provides a structured way to revisit the material repeatedly.

Focus on Core Concepts

To make the most of your practice, start by focusing on the fundamental principles that are essential to solving most problems. Understanding the core concepts will make it easier to tackle more advanced questions later on. Work through practice problems that focus on these fundamental ideas until you feel comfortable with them.

• Master Basic Formulas: Practice using key equations until they become second nature.
• Review Core Theorems: Familiarize yourself with the most important rules and postulates that govern the subject.
• Strengthen Visualization Skills: Work on visualizing shapes and their properties to improve your understanding of geometric relationships.

Identify Patterns in Problem Types

As you review practice problems, look for recurring problem types. Often, the same concepts appear in different forms, and identifying these patterns will help you anticipate what might appear in a real assessment. Practice answering similar problems so that you can confidently approach these familiar types without hesitation.

• Recognize Common Structures: Learn to quickly identify common figure types and how to approach solving them.
• Understand Problem Formats: Focus on how questions are framed and how to extract the relevant information.
• Practice with Similar Scenarios: Repetition of similar problems allows you to refine your skills and build familiarity with various question styles.

Time Your Practice Sessions

To make your review even more effective, time yourself during practice. Simulating the time constraints of the actual assessment can help you develop time management skills and prepare you for the pressure of working under a clock. Try to solve a set of problems within a set time limit to build both speed and accuracy.

• Set Time Limits: Use a timer to mimic the actual conditions and prevent yourself from spending too much time on any one problem.
• Track Progress: Measure how long it takes you to complete a practice set and aim to improve your speed over time.
• Evaluate Your Efficiency: Check your work afterward to see if you can complete the problems faster or with fewer errors in the future.

Tips for Geometry Word Problems

Word problems can be one of the most challenging parts of any assessment, as they require not only mathematical skills but also the ability to translate a real-world scenario into a solvable problem. The key to mastering these types of questions is developing a clear strategy for approaching them. With a structured approach, you can break down complex situations and solve them step by step.

The first step in solving word problems is to carefully read the problem multiple times. Understanding the scenario and identifying the important information is crucial. Often, word problems contain extra details meant to distract you, so focus on the numbers and relationships that are directly relevant to the question.

Step 1: Highlight Important Information

Before beginning to solve a problem, underline or highlight the key facts and numbers. This will help you quickly identify what information you need to use in your calculations. Pay attention to units of measurement, relationships between different elements, and any specific instructions that guide the steps of the solution.

• Look for Key Numbers: Focus on the quantities given, such as lengths, areas, and angles.
• Identify Relationships: Understand how the numbers are connected, whether they describe proportions, angles, or distances.
• Note Units: Be mindful of the units used (meters, feet, degrees) and convert them if necessary.

Step 2: Draw a Diagram

Whenever possible, draw a diagram to represent the situation. A visual representation can help you better understand the relationships between different elements and give you a clearer picture of the problem. This step can make it easier to see how the different parts of the problem fit together.

• Sketch the Figure: Draw out any shapes, lines, or angles described in the problem.
• Label the Diagram: Mark all known values, such as side lengths or angles, directly on your drawing.
• Visualize Relationships: Look for geometric relationships, such as parallel lines or symmetry, that can help you simplify the problem.

Step 3: Translate Words into Equations

Once you have a good understanding of the problem and a diagram to work with, the next step is to translate the word problem into mathematical equations. Identify the unknowns and use the relationships you’ve identified to form equations. This is where knowing the relevant formulas and principles comes into play, as they will guide your calculations.

• Formulate Equations: Use known relationships, such as Pythagoras’ theorem or properties of angles, to create equations.
• Solve for Unknowns: Solve the equations systematically, paying close attention to any steps that might require simplification or factoring.
• Check for Units: Ensure that your solution matches the units used in the problem and convert as needed.

Step 4: Verify Your Solution

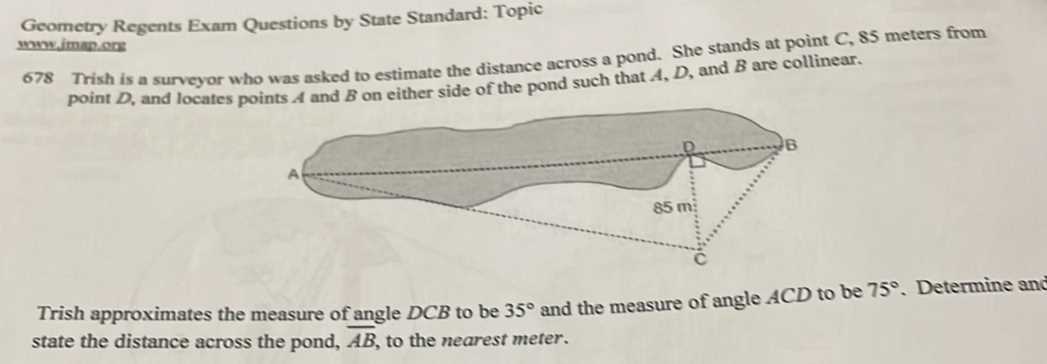
After solving the problem, always take the time to check your work. Review your calculations, ensure that you haven’t made any arithmetic errors, and confirm that your solution makes sense in the context of the problem. A good habit is to revisit the original word problem and make sure your final answer addresses the question asked.

• Double-Check Calculations: Look over each step of your solution to catch any potential mistakes.
• Ensure Logical Consistency: Make sure your solution fits logically with the information provided in the problem.
• Revisit the Question: Make sure your final answer actually answers the question posed in the problem.

Using Diagrams Effectively in Geometry

Diagrams are powerful tools in solving mathematical problems, especially when they provide a visual representation of complex relationships. By translating abstract concepts into tangible images, diagrams allow you to better understand the problem and identify key information. A well-drawn diagram can simplify even the most complicated scenarios, helping you to organize and solve problems with greater clarity.

The first step in using diagrams effectively is to accurately represent the situation described in the problem. Pay attention to the shapes, angles, distances, and other relevant elements mentioned. Even if the problem doesn’t explicitly ask for a diagram, drawing one can help you to visualize the situation more clearly.

Once the diagram is drawn, labeling it becomes an essential step. Labeling helps connect the given information with your diagram, making it easier to work with. Mark all known values, such as side lengths, angles, and any other details provided in the problem. If the diagram involves specific points, lines, or figures, label these as well for easy reference.

Another key aspect of using diagrams is identifying hidden relationships between the elements of the problem. For example, if two lines are parallel or if certain angles are congruent, marking these properties on the diagram can help guide your solution process. Recognizing symmetries, parallelism, or perpendicularity can reveal shortcuts for solving the problem efficiently.

As you solve the problem, keep referring back to the diagram. Sometimes, you may notice additional relationships or patterns that you missed during the initial analysis. Use the diagram as a tool to check your progress and to ensure that each step is consistent with the visual representation.

Geometry Questions on Congruence and Similarity

Understanding the principles of congruence and similarity is crucial when solving geometric problems. These concepts form the foundation for comparing shapes, determining their relationships, and solving various types of geometric problems. Whether dealing with triangles, quadrilaterals, or other polygons, recognizing when figures are congruent or similar can simplify the solution process significantly.

Congruence refers to figures that are identical in shape and size. In other words, two objects are congruent if you can match them exactly by placing one on top of the other. To prove that two shapes are congruent, certain conditions need to be satisfied, such as corresponding sides being equal in length and corresponding angles being equal. For triangles, there are several theorems that help establish congruence, such as the Side-Side-Side (SSS) Postulate, the Side-Angle-Side (SAS) Postulate, and others.

Similarity in Geometric Shapes

On the other hand, similarity deals with shapes that have the same form but may differ in size. Two figures are similar if their corresponding angles are equal, and the lengths of their corresponding sides are proportional. This concept allows for the use of scale factors, which describe how one figure can be resized to match another. The properties of similar figures are widely used in real-world problems, such as finding unknown distances or heights in geometric settings.

Applications of Congruence and Similarity

These concepts are frequently used in problem-solving situations. For example, in construction, architects use similarity to scale models of buildings to full size, ensuring all proportions remain accurate. In contrast, congruence is used to match parts or pieces exactly, ensuring they fit together properly, such as in manufacturing or design.

When solving problems involving congruence and similarity, it’s important to carefully analyze the figures and look for key properties like side lengths, angle measures, and scale factors. Using the correct theorems and reasoning can help identify these relationships and lead to the solution efficiently.

Advanced Geometry Topics for Regents Exam

As you advance in your studies, you’ll encounter more complex concepts that require a deeper understanding of spatial relationships and mathematical reasoning. These higher-level ideas are essential for mastering challenging problems and applying principles in real-world scenarios. Gaining proficiency in these advanced areas can give you the tools needed to tackle difficult questions effectively and with confidence.

Some of the more advanced areas of study include topics that build on basic principles but involve more intricate reasoning, proofs, and applications. Mastery of these concepts can set you apart and ensure you are well-prepared for any higher-level mathematical problems. Below are key areas that often appear in more advanced levels of study:

Coordinate Geometry and Transformations

Understanding the relationship between algebraic equations and geometric shapes is crucial in higher mathematics. Coordinate geometry combines algebra and geometry to solve problems involving distances, midpoints, and slopes. Transformations, such as translations, rotations, reflections, and dilations, also play an important role in geometric reasoning. Recognizing how to manipulate and analyze geometric objects in a coordinate plane is vital for solving many problems.

• Distance Formula: Used to find the distance between two points in a coordinate plane.
• Slope Formula: Helps determine the steepness of a line and is essential for analyzing parallel and perpendicular lines.
• Midpoint Formula: Used to find the center point between two coordinates.
• Transformations: Understand how figures change under various manipulations, including dilations, reflections, and rotations.

Proofs and Logical Reasoning

Another important aspect of advanced geometry involves constructing logical arguments and proofs. These require you to demonstrate why certain geometric relationships hold true under specific conditions. Proofs help in validating theorems and properties and are central to understanding how theorems are applied. There are several proof techniques, such as direct proofs, indirect proofs, and proofs by contradiction, all of which are essential for solving complex problems.

• Direct Proofs: Involves straightforward reasoning from premises to conclusion.
• Indirect Proofs: Uses a method where you assume the opposite of what you’re trying to prove and show that this assumption leads to a contradiction.
• Proof by Contradiction: Assumes that the statement to be proven is false and works towards a contradiction to prove it must be true.

Mastering these advanced topics will allow you to approach even the most challenging problems with a solid foundation of knowledge and logical thinking. With continuous practice and a clear understanding of these concepts, you will be better prepared to handle a wide variety of questions and apply your mathematical skills effectively in real-world situations.

How to Check Your Geometry Answers

After working through a set of problems, it is essential to verify that your results are correct. This process helps ensure that you haven’t overlooked any details or made simple mistakes during calculations. Checking your work not only helps you catch errors but also strengthens your understanding of key concepts and problem-solving techniques.

Here are some strategies to ensure your solutions are accurate and reliable:

• Review the Problem Statement: Carefully reread the question to make sure you understand what is being asked. Look for specific requirements or constraints in the problem that might guide your solution method.
• Double-Check Your Calculations: Go through each step of your solution again to make sure your calculations are correct. Pay special attention to arithmetic operations and formula usage.
• Use Alternative Methods: If possible, solve the problem in more than one way. This can help verify that your initial approach is correct. For example, if you used algebraic methods, try solving it with geometric reasoning and vice versa.
• Check Units and Measurements: Ensure that you have used consistent units throughout the solution and that any conversions (e.g., from centimeters to meters) were done properly. This is especially important for problems involving measurements or real-world applications.
• Estimate Your Answer: Before finalizing your solution, make a rough estimate of what the answer should be. This mental check can help you spot unreasonable answers or prevent you from missing key steps.

By employing these techniques, you can feel more confident in your results and reduce the likelihood of errors in your work. Regular practice and attention to detail will help improve your problem-solving skills and ensure that your answers are as accurate as possible.

Resources for Additional Geometry Practice

To deepen your understanding and sharpen your skills, using supplementary materials can be extremely helpful. These resources offer a variety of methods and approaches that cater to different learning styles, providing ample opportunities for reinforcing concepts and honing problem-solving abilities. Whether you’re looking for practice sets, interactive exercises, or instructional videos, there are many options available to support your preparation.

Online Platforms and Websites

Numerous websites offer extensive practice problems, step-by-step solutions, and detailed explanations. These resources are excellent for reinforcing your knowledge and providing immediate feedback on your work. Some sites also offer timed practice to simulate real testing environments.

• Khan Academy: Offers free video lessons and exercises on a wide range of mathematical concepts. Each lesson includes interactive quizzes to test your understanding.
• IXL: Provides personalized practice problems and immediate feedback. It adapts to your level of proficiency and helps track your progress.
• Brilliant.org: Focuses on building problem-solving skills through interactive courses and challenges designed to test and enhance your critical thinking abilities.

Books and Study Guides

Textbooks and study guides are timeless resources that provide structured practice in various topics. These materials often contain a mixture of conceptual explanations, practice problems, and examples, all carefully organized to guide learners from basic to advanced topics.

• Practice Workbooks: Many publishers offer dedicated workbooks filled with practice problems that cover all essential areas. These books are often organized by difficulty level to help you progress step by step.
• Study Guides: Books like “The Princeton Review” and “Barron’s” offer comprehensive review sections, practice questions, and strategies for tackling complex problems efficiently.

Incorporating a variety of resources into your routine will not only reinforce your understanding of key concepts but also help you become more adaptable in solving diverse types of problems. Regular practice and exposure to different problem-solving techniques will ensure you’re well-prepared for any challenge.