Geometry Chapter 1 Worksheet Answers

In this section, we will explore foundational concepts and key skills necessary for tackling fundamental exercises in mathematics. Understanding the core principles is essential for building a strong foundation in problem-solving and applying mathematical reasoning effectively.

By practicing and reviewing step-by-step methods, you will enhance your ability to approach complex challenges with confidence. Through clear explanations and guided examples, we aim to simplify the learning process and help you grasp the material more thoroughly.

With a focus on precision and clarity, this guide is designed to support you in mastering the essential techniques needed to solve problems accurately and efficiently. Whether you are reinforcing your skills or tackling new topics, these tools will aid in your progress.

Geometry Chapter 1 Worksheet Answers

In this section, we will dive into the essential exercises that help reinforce key mathematical concepts and improve problem-solving skills. By breaking down each challenge, you will better understand the methods needed to find solutions and gain confidence in your abilities.

Step-by-Step Explanation of Key Problems

Breaking down each problem into manageable steps makes it easier to tackle and understand. Below, we’ve provided a structured approach to common exercises, showing how each method leads to the correct solution.

Problem	Solution Method	Result
Find the area of a rectangle with length 5 cm and width 3 cm	Multiply length by width: 5 × 3 = 15 cm²	Area = 15 cm²
Calculate the perimeter of a triangle with sides 4 cm, 6 cm, and 8 cm	Add all sides together: 4 + 6 + 8 = 18 cm	Perimeter = 18 cm

Tips for Solving Similar Problems

When faced with similar types of questions, it’s helpful to apply the same logic and techniques consistently. Pay attention to the shapes and measurements provided, and remember to break the problem down into smaller, simpler parts to make solving it more straightforward.

Understanding Basic Geometry Concepts

Mastering the foundational ideas behind shapes, lines, and measurements is crucial for tackling more advanced mathematical challenges. A solid grasp of these essential principles allows you to approach various problems with confidence and clarity, providing a strong base for future learning.

Key concepts include the properties of different figures, such as angles, sides, and symmetry. By recognizing these characteristics, you can quickly identify patterns and relationships that help in solving a wide range of problems.

For example, understanding the relationship between the sides and angles of triangles or the formulas for calculating areas and perimeters is a critical skill that applies to many mathematical situations. Whether dealing with polygons, circles, or other shapes, the ability to analyze their properties systematically leads to accurate solutions.

Additionally, becoming familiar with terms such as vertices, edges, and faces helps you navigate through more complex problems. The more you practice identifying and working with these elements, the easier it becomes to solve related tasks and apply these concepts in real-world scenarios.

Key Theorems in Geometry Chapter 1

In any study of mathematics, understanding fundamental theorems is essential for problem-solving and logical reasoning. These theorems provide a framework for understanding how different elements in a shape or figure relate to each other, guiding you through a variety of tasks and calculations.

Below are some of the most important principles to master early on:

• The Pythagorean Theorem: This theorem establishes the relationship between the sides of a right triangle, stating that the square of the hypotenuse equals the sum of the squares of the other two sides.
• Angle Sum Property: The sum of the interior angles of any triangle is always 180 degrees. This principle helps determine unknown angles when working with triangular shapes.
• Properties of Parallel Lines: When two parallel lines are cut by a transversal, several angle relationships are formed, such as alternate interior angles being equal and corresponding angles being congruent.

By thoroughly understanding these key theorems, you’ll gain the tools to approach and solve a wide range of mathematical problems with confidence.

Step-by-Step Solutions for Geometry Exercises

Solving mathematical problems becomes easier when broken down into manageable steps. A systematic approach not only makes complex tasks more understandable but also helps to ensure accuracy in your calculations. Below, we’ll walk through several examples using clear and structured methods that can be applied to a variety of problems.

Example 1: Finding the Area of a Rectangle

To find the area of a rectangle, you simply multiply the length by the width. For instance, if the length is 8 units and the width is 5 units, the area would be:

Area = length × width

Area = 8 × 5 = 40 square units

Example 2: Calculating the Perimeter of a Triangle

The perimeter of a triangle is the sum of the lengths of its three sides. If a triangle has sides measuring 3 cm, 4 cm, and 5 cm, the perimeter would be:

Perimeter = side1 + side2 + side3

Perimeter = 3 + 4 + 5 = 12 cm

By following these steps, you can solve similar problems quickly and effectively, ensuring that you understand the underlying principles behind each solution.

Common Mistakes in Geometry Worksheets

While working through mathematical problems, it’s easy to make certain errors that can lead to incorrect solutions. Identifying and understanding these mistakes is essential for improving problem-solving skills and avoiding repeated errors. Below are some of the most common pitfalls students encounter when solving problems related to shapes, measurements, and calculations.

Common Errors to Avoid

• Misinterpreting the Question: Sometimes, the problem may ask for a specific measurement or property, and it’s easy to confuse it with another value, such as calculating area instead of perimeter.
• Incorrect Application of Formulas: Using the wrong formula for a specific type of figure is a common mistake. For example, applying the area formula for a triangle to a rectangle.
• Forgetting Units of Measurement: It’s important to include the correct units when calculating answers. Leaving them out can result in incomplete or unclear solutions.
• Not Double-Checking Calculations: Simple arithmetic mistakes, such as addition or multiplication errors, can lead to wrong answers. Always double-check each step to ensure accuracy.

How to Avoid These Mistakes

1. Read the Problem Carefully: Always take the time to understand exactly what is being asked before starting to solve the problem.
2. Know the Correct Formulas: Familiarize yourself with the formulas relevant to different shapes and always ensure you’re using the appropriate one for each problem.
3. Use a Systematic Approach: Break down the problem into smaller, manageable parts and solve step by step to minimize mistakes.

By being aware of these common errors and practicing attention to detail, you can improve your problem-solving accuracy and gain confidence in tackling more challenging tasks.

Key Terms You Should Know

Understanding the fundamental vocabulary is essential for working through mathematical problems efficiently. Familiarity with key terms helps you identify the properties of different shapes, relationships between angles, and methods for solving various types of problems. Below are some important concepts that are commonly used in this field.

Basic Terms to Get Started

• Angle: The space between two intersecting lines, usually measured in degrees.
• Vertex: The point where two lines or sides meet, forming an angle.
• Side: A straight line that forms part of the boundary of a shape or figure.
• Perimeter: The total length around the boundary of a two-dimensional shape.
• Area: The amount of space inside a shape, typically measured in square units.

Advanced Terms for Deeper Understanding

• Parallel Lines: Two lines that run in the same direction and are equidistant from each other, never meeting.
• Congruent: When two shapes or figures are identical in size and shape.
• Symmetry: The property of a shape that allows it to be divided into two identical parts by a line or plane.
• Radius: The distance from the center of a circle to any point on its boundary.
• Hypotenuse: The longest side of a right triangle, opposite the right angle.

By mastering these terms, you’ll have a solid foundation for solving problems and understanding more complex concepts as you progress.

How to Solve Geometry Problems Effectively

Solving mathematical challenges requires a strategic approach to ensure accuracy and efficiency. By following a clear process, you can break down complex problems into manageable steps, making them easier to understand and solve. Here are some tips to help you approach these problems with confidence and precision.

First, it’s important to thoroughly read the problem and understand what is being asked. Identify the key elements, such as the shapes, dimensions, and relationships between different components. Once you have a clear understanding, decide which formula or method applies to the situation. This step is crucial for selecting the right approach to solve the problem.

Next, break the problem into smaller steps. Don’t try to solve it all at once–start with the simplest calculations and build up. Keep track of your work, checking each step for accuracy. This method not only prevents errors but also helps you understand the reasoning behind each calculation.

Finally, always double-check your final answer to ensure it makes sense within the context of the problem. Revisiting your work and verifying the solution can help you catch mistakes that might have been overlooked initially.

Tips for Mastering Geometry Concepts

Mastering mathematical concepts requires both understanding the theory and practicing application. Success comes from building a strong foundation, reinforcing key ideas, and developing problem-solving strategies. Below are some effective tips to help you become more proficient in working with shapes, angles, and spatial relationships.

Focus on Understanding, Not Memorization

While it’s important to know formulas, true mastery comes from understanding why those formulas work. Focus on grasping the relationships between different elements of shapes and figures. This deeper understanding will help you solve problems more effectively, even when the questions are phrased differently.

Practice Regularly to Build Confidence

Repetition is key to mastering any skill. The more problems you work through, the more familiar you will become with the various methods and formulas. Practice different types of problems to ensure that you are comfortable with all aspects of the topic.

Strategy	Description
Draw Diagrams	Visualizing the problem can help you better understand the relationships between different elements and make calculations easier.
Break Problems into Steps	Start by identifying the simplest knowns and build up to find unknowns. This approach minimizes errors and ensures clarity.
Review Mistakes	Look back at incorrect answers to understand where you went wrong, and try to avoid making the same mistake again.

By combining these strategies with consistent practice, you can improve your ability to solve problems and strengthen your overall grasp of key concepts.

Helpful Resources for Geometry Practice

Effective learning often involves utilizing a variety of resources that can enhance your understanding and provide additional practice. From online platforms to textbooks, there are many tools available that can help reinforce key concepts and improve problem-solving skills. Below are some useful resources that can help you strengthen your abilities in tackling mathematical challenges.

1. Online Learning Platforms: Websites like Khan Academy and Coursera offer free courses and tutorials on a wide range of mathematical topics. These platforms provide step-by-step explanations, interactive exercises, and video lessons, making it easier to grasp complex concepts.

2. Practice Problems Websites: Platforms such as IXL or Brilliant allow you to practice problems at different levels of difficulty. These sites also provide instant feedback, helping you learn from your mistakes and improve your skills over time.

3. Educational Apps: Many apps are designed to help you practice problem-solving on the go. Apps like Photomath and Wolfram Alpha can assist in solving specific problems while explaining the steps involved in each solution.

4. Textbooks and Study Guides: Comprehensive textbooks often provide a wide range of examples and practice problems, along with detailed explanations. Study guides and reference books can also help clarify difficult concepts and provide additional practice questions.

5. Peer Study Groups: Sometimes discussing problems with others can provide new insights. Study groups, whether in person or online, offer a collaborative way to solve problems together, share techniques, and learn from one another.

By exploring these resources and consistently practicing, you can improve your skills and gain confidence in solving mathematical problems.

Visualizing Problems and Solutions

When faced with mathematical challenges, visualization is a powerful tool that can help clarify complex situations. By creating a mental or physical image of the problem, you can better understand the relationships between different elements, making it easier to find a solution. Visual aids such as diagrams, graphs, and sketches often simplify the problem-solving process.

One effective approach is to draw the figures involved in the problem. Whether it’s a triangle, a circle, or any other shape, seeing the components visually can help you grasp their connections. Once the image is in front of you, labeling key points, lines, and angles can provide additional clarity and guide your reasoning.

In many cases, breaking down the problem into smaller, more manageable parts is crucial. This allows you to focus on one element at a time and gradually work toward the solution. Visualizing these steps can prevent you from feeling overwhelmed and keep you on track as you solve the problem.

Additionally, tools like graphing calculators and interactive software can provide dynamic visual representations of problems. These resources are particularly useful for exploring different scenarios and understanding how changes to one element affect the overall situation.

Overall, developing the skill to visualize mathematical problems can enhance both comprehension and problem-solving efficiency. By incorporating this technique into your study routine, you’ll be better equipped to tackle even the most challenging problems.

Exploring Real-World Applications

Mathematics isn’t just an abstract subject confined to textbooks–it’s a tool used in various real-life situations. From architecture to engineering, the principles you learn in solving problems can be applied to create and understand the world around us. The ability to solve spatial problems and understand shapes, sizes, and relationships plays a crucial role in a variety of fields.

In construction, for example, precise measurements and calculations are necessary to design buildings, bridges, and other structures. Engineers rely on these principles to ensure that the structures they build are stable and functional. Similarly, in the field of art and design, understanding spatial relationships allows artists to create realistic works or design functional, aesthetically pleasing objects.

Additionally, many technological innovations, including computer graphics and robotics, rely on principles of spatial reasoning. Whether it’s designing virtual environments for video games or creating movements in robotics, understanding the properties of shapes and how they interact in space is essential.

In everyday life, geometry can also help with tasks like organizing space efficiently, from arranging furniture in a room to optimizing the layout of a garden. By applying the same principles, you can improve practical problem-solving and spatial awareness in daily activities.

By exploring the real-world applications of mathematical principles, you can gain a deeper appreciation for their relevance and importance. These skills are not only valuable in academic contexts but also in making decisions and solving problems in various careers and everyday scenarios.

Improving Your Problem-Solving Skills

Enhancing your ability to tackle mathematical problems requires a combination of practice, strategy, and a solid understanding of fundamental principles. Developing strong problem-solving skills not only helps with academic success but also fosters critical thinking and logical reasoning. Below are several effective methods to improve your approach to solving problems in mathematics.

• Understand the Problem: Carefully read through the problem and ensure you grasp what is being asked. Break it down into smaller, manageable parts if necessary.
• Identify Key Information: Highlight or write down important details such as numbers, shapes, and relationships that are critical to finding a solution.
• Visualize the Situation: Draw diagrams or sketches to help represent the problem. This allows you to see the relationships between different elements more clearly.
• Use Logical Steps: Approach each problem in a systematic way. Identify the steps that logically lead to a solution, and follow them one at a time.
• Practice Regularly: The more problems you solve, the better you become at recognizing patterns and applying appropriate techniques. Consistent practice is key to mastering any skill.
• Review Mistakes: After solving a problem, revisit any mistakes or challenges you encountered. Understand why an approach didn’t work and how you can improve next time.

By implementing these strategies and consistently practicing, you’ll gradually become more confident and efficient in solving problems. Problem-solving is a skill that can be honed with time, and the more you practice, the more intuitive it becomes.

Explaining Key Definitions

Understanding the foundational terms used in mathematics is essential for building problem-solving skills and grasping more advanced concepts. Whether working with shapes, angles, or spatial relationships, having a clear understanding of the key definitions allows you to approach challenges with confidence and clarity. Below are some important terms and their meanings that serve as building blocks in mathematical reasoning.

• Point: A point represents a specific location in space. It has no width, length, or depth, only position.
• Line: A line is a one-dimensional figure that extends infinitely in both directions. It is made up of an infinite number of points connected in a straight path.
• Angle: An angle is formed by two rays or lines that share a common endpoint, called the vertex. The amount of rotation between the two rays determines the angle’s measure.
• Parallel Lines: Parallel lines are lines that never intersect and remain equidistant from each other throughout their length.
• Perpendicular Lines: Perpendicular lines are lines that intersect at a right angle (90 degrees) to each other.
• Triangle: A triangle is a three-sided polygon formed by connecting three non-collinear points with straight lines. It has three angles, and the sum of these angles always equals 180 degrees.

These definitions serve as the foundation for understanding more complex concepts and problem-solving strategies. By familiarizing yourself with these basic terms, you create a strong base for tackling mathematical challenges with greater ease and accuracy.

How to Approach Word Problems

Word problems in mathematics often require a combination of reading comprehension and logical reasoning. The goal is to translate the information provided in a verbal format into a mathematical framework that can be solved systematically. By following a series of steps, you can break down complex scenarios into manageable parts and identify the best approach to find a solution.

Steps to Solve Word Problems

Start by understanding the situation described in the problem. Carefully read the text and identify key information such as numbers, relationships, and any conditions that apply. Once you’ve gathered the necessary details, it’s time to translate them into mathematical terms. Here’s a general approach to tackling word problems:

1. Read the problem carefully: Understand what is being asked and identify the known values and unknowns.
2. Visualize the scenario: If possible, draw a diagram or sketch that represents the situation. This helps you see the relationships between different elements more clearly.
3. Set up equations: Translate the word problem into mathematical equations based on the relationships described in the problem.
4. Solve the equations: Use appropriate mathematical techniques to solve for the unknown values.
5. Check your solution: Ensure that your answer makes sense in the context of the problem and double-check your calculations.

Example of a Word Problem

Here’s an example to illustrate the process:

Problem	Solution
Find the perimeter of a rectangle with a length of 10 units and a width of 5 units.	The perimeter of a rectangle is calculated by the formula: P = 2 × (length + width). Substituting the given values: P = 2 × (10 + 5) = 2 × 15 = 30 units.

By following these steps, you can approach word problems methodically and solve them more effectively. Practicing this approach will improve your problem-solving skills over time.

Review of Important Postulates

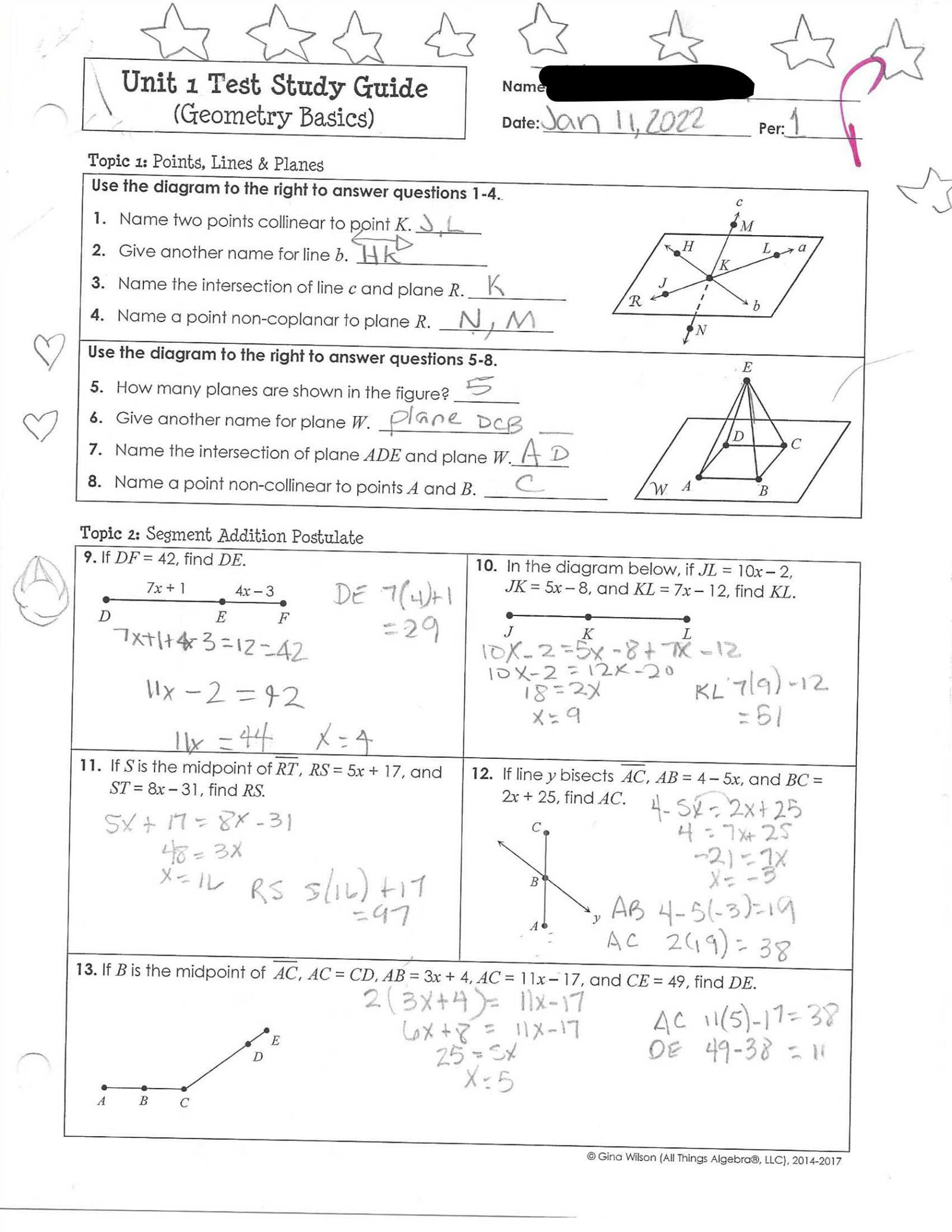
In mathematics, postulates serve as the foundational principles upon which further reasoning and theorems are built. These basic assumptions are accepted as true without the need for proof and provide the necessary framework for solving problems and understanding relationships. A solid understanding of these key postulates is essential for working through various problems and constructing logical arguments in mathematical contexts.

Key Postulates You Should Know

Below is a list of fundamental postulates that are frequently used in solving problems:

• Postulate 1: Through any two distinct points, there is exactly one straight line.
• Postulate 2: A line segment can be extended indefinitely in both directions.
• Postulate 3: All right angles are congruent.
• Postulate 4: If two lines intersect, they do so at exactly one point.
• Postulate 5: Through any three non-collinear points, there is exactly one plane.

How to Use Postulates Effectively

Understanding and applying these postulates is key to solving more complex problems. Here are some strategies to help you use postulates effectively:

1. Start with simple relationships: Use the basic postulates to identify simple geometric relationships before attempting more complicated reasoning.
2. Check consistency: Postulates help ensure that your reasoning is consistent. When you encounter contradictions, recheck your assumptions and apply relevant postulates.
3. Apply them to proofs: Postulates are often used as the starting point for logical proofs, so it’s important to be familiar with them to build your arguments step by step.

Mastering these postulates will provide a solid foundation for tackling a variety of problems and help you approach more complex mathematical ideas with confidence.

Strategies for Test Preparation

Preparing for a test requires a focused approach, especially when dealing with subjects that involve logical reasoning and problem-solving. Developing a clear understanding of the fundamental concepts and practicing regularly can make a significant difference in your performance. Effective preparation strategies will help you tackle different types of problems and strengthen your confidence before the test.

Effective Study Techniques

To improve your test performance, consider implementing the following strategies:

• Review Core Concepts: Start by revisiting the fundamental concepts and definitions. Make sure you understand key terms and postulates that form the foundation of the subject.
• Practice Regularly: Solve a variety of problems from different topics. The more you practice, the more familiar you’ll become with different problem types and methods of solving them.
• Create Summary Notes: Write concise notes summarizing important formulas, theorems, and techniques. This will help with quick revision and reinforce your understanding.
• Work Through Sample Problems: Practice solving problems that are similar to those you expect to encounter on the test. This allows you to test your skills and identify areas where you may need further improvement.

Time Management and Focus

Effective time management is crucial during both preparation and the test itself:

• Set a Study Schedule: Break your study time into manageable sessions. Avoid cramming the night before, and instead spread out your revision over several days or weeks.
• Stay Focused: Minimize distractions while studying and take regular breaks to refresh your mind. Staying focused during practice will help build your problem-solving speed and accuracy.
• Simulate Test Conditions: Take timed practice tests to simulate real exam conditions. This helps you manage time effectively and get comfortable with the test format.

By combining consistent practice, a deep understanding of key concepts, and effective time management, you will be well-equipped to succeed in your upcoming test.

Understanding Formulas and Equations

In any subject involving shapes and spatial relationships, formulas and equations serve as essential tools for solving problems and finding unknown values. Mastery of these mathematical expressions is crucial for successfully navigating through various types of problems. Whether it’s calculating the area of a figure, determining the length of a side, or solving for an unknown angle, a strong understanding of the formulas at hand is vital.

Key to Success: Each formula is derived from fundamental principles and relationships between different elements. It’s important not just to memorize these equations but to understand their underlying concepts and how they apply to real-world situations. This approach helps in quickly identifying which formula to use and how to manipulate it when necessary.

Commonly Used Formulas

Some of the most commonly used formulas in solving problems include:

• Area of a Rectangle: Area = length × width
• Perimeter of a Square: Perimeter = 4 × side
• Circumference of a Circle: Circumference = 2 × π × radius
• Volume of a Rectangular Prism: Volume = length × width × height
• Pythagorean Theorem: a² + b² = c²

Applying Formulas in Problem-Solving

To apply these formulas effectively, it’s crucial to identify the key information provided in the problem. From there, you can substitute the known values into the appropriate formula. For example, if you are asked to find the area of a triangle, you would first identify the base and height, then apply the formula for area: Area = ½ × base × height.

Understanding how to rearrange and adapt formulas is another important skill. Sometimes, you might need to solve for a different variable, so knowing how to isolate the desired value is essential. With consistent practice, these equations become intuitive, and you will be able to solve problems with greater speed and accuracy.

Additional Practice for Mastering Key Concepts

To truly grasp the foundational principles of working with shapes, spatial relationships, and measurements, it is essential to engage in additional exercises beyond initial lessons. This practice helps reinforce your understanding and improves your ability to apply what you’ve learned in various contexts. Repetition and application are key to mastering any mathematical discipline.

Exercises for Solidifying Understanding

Below are a series of exercises that target different aspects of problem-solving. These problems will allow you to deepen your knowledge of key concepts and improve your confidence in using formulas, theorems, and logical reasoning to solve complex tasks.

• Find the area of a parallelogram with a base of 8 cm and a height of 5 cm.
• Determine the perimeter of a triangle with sides measuring 6 cm, 7 cm, and 8 cm.
• Use the Pythagorean theorem to find the hypotenuse of a right triangle with legs measuring 9 cm and 12 cm.
• Calculate the volume of a cylinder with a radius of 4 cm and a height of 10 cm.
• Find the circumference of a circle with a diameter of 14 cm.

Tips for Success

When tackling these problems, ensure that you carefully read each question and identify the relevant measurements and relationships between the elements involved. Don’t rush the process–take the time to set up the correct formula and work step-by-step. Over time, with continued practice, you’ll improve both your speed and accuracy.

Additionally, reviewing your mistakes and understanding why certain approaches didn’t work will help strengthen your problem-solving strategies. Use these practice problems regularly to develop a deeper understanding and boost your performance.