Algebra 1 Final Exam Review Guide

As you approach the culmination of your studies in mathematics, it’s essential to refresh your knowledge of the core concepts that will be tested. This guide will help you focus on the most important areas, offering a structured path to ensure you feel confident on test day.

Whether it’s solving equations, graphing functions, or simplifying expressions, understanding the underlying principles is crucial. Strengthening these skills will not only prepare you for this assessment but also provide a solid foundation for future learning.

Throughout this guide, we’ll highlight effective strategies, common pitfalls to avoid, and practice exercises to help reinforce key topics. By breaking down each area into manageable sections, you’ll be able to approach the test with a clear plan and a greater sense of readiness.

Mathematics Assessment Preparation

In the final stages of your studies, reviewing the key concepts and techniques is essential to achieving success. This section focuses on the most critical areas of your course, providing targeted practice and strategies to help you approach the test with confidence.

Core Topics to Focus On

• Linear equations and their solutions
• Systems of equations and methods for solving them
• Graphing and interpreting different types of functions
• Working with exponents and powers
• Solving word problems efficiently

Effective Study Strategies

• Break down complex problems into smaller steps
• Review past assignments and practice problems
• Practice time management during mock tests
• Focus on areas of weakness and seek additional help if needed
• Reinforce understanding with interactive tools or online resources

By focusing on these areas and employing effective study techniques, you will be well-prepared for the upcoming assessment and ready to tackle any challenge that comes your way.

​

Understanding Linear Equations

Mastering the concept of equations with a single variable is fundamental for solving many mathematical problems. These types of expressions represent relationships between variables and can be solved through various methods. Developing a clear understanding of how to manipulate and solve these equations will help you tackle more complex challenges in the future.

To begin, it’s important to recognize the general form of such equations. They typically include constants and variables, often written in the form of ax + b = c, where a, b, and c are constants, and x is the variable to solve for. Solving these equations involves isolating x on one side.

Here are the key steps to solving linear equations:

• Identify the variable and constants in the equation.
• Apply the appropriate operations to isolate the variable on one side.
• Simplify both sides of the equation to find the solution.

Consistent practice with linear equations will increase your ability to solve them quickly and accurately, paving the way for more advanced topics.

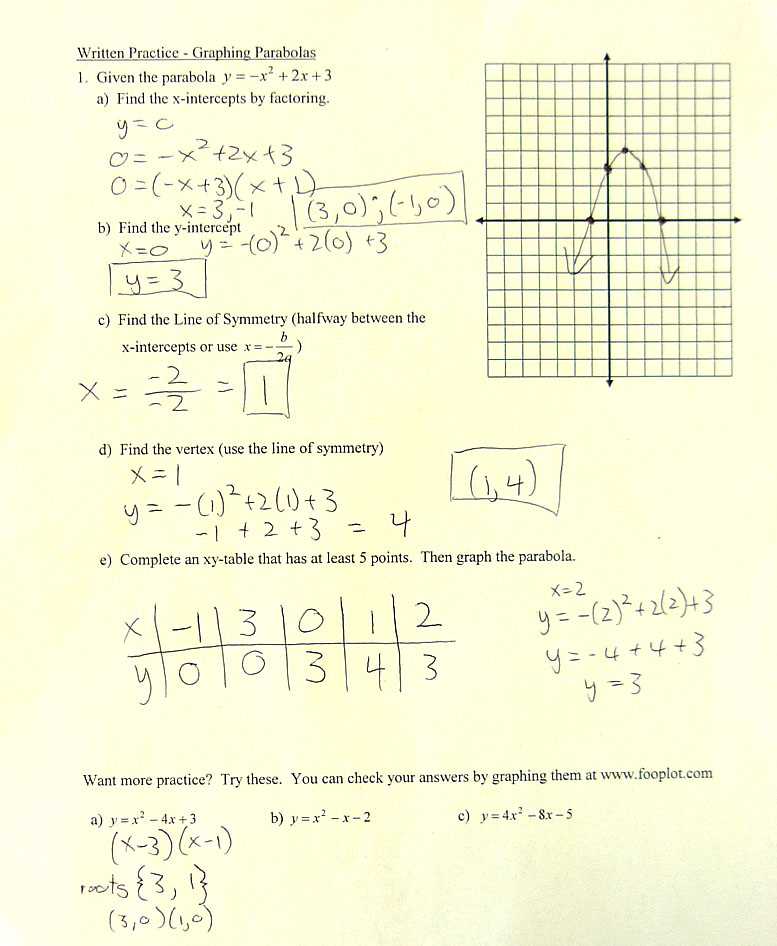
Mastering Quadratic Functions

Quadratic functions are fundamental to understanding more advanced mathematical concepts. These functions, which form a parabolic curve when graphed, play a key role in various fields of study, including physics, engineering, and economics. Gaining proficiency in working with them will enhance your problem-solving skills and prepare you for future challenges.

Key Characteristics of Quadratic Functions

• Standard form: y = ax² + bx + c, where a, b, and c are constants.
• The graph is a parabola, which opens upwards or downwards depending on the value of a.
• The vertex is the highest or lowest point on the graph, depending on the direction of the parabola.

Solving Quadratic Equations

• Factoring: Finding two binomials whose product equals the quadratic expression.
• Quadratic formula: x = (-b ± √(b² – 4ac)) / 2a.
• Completing the square: Rewriting the equation to form a perfect square trinomial.

By practicing these methods and understanding the graphical representation of quadratic functions, you will be able to approach more complex problems with confidence and accuracy.

Solving Systems of Equations

Systems of equations involve finding the values of variables that satisfy multiple equations simultaneously. These problems often appear in real-life situations where different conditions must be met at the same time. Understanding how to solve them is crucial for tackling more complex mathematical scenarios.

There are several methods for solving systems of equations, each with its own advantages depending on the specific problem. Whether you’re dealing with linear equations or a mix of different types, mastering these techniques will greatly improve your ability to solve related problems efficiently.

• Graphing method: Plot both equations on a graph and find the point where the lines intersect.
• Substitution method: Solve one equation for a variable and substitute this expression into the other equation.
• Elimination method: Add or subtract the equations to eliminate one variable, then solve for the remaining variable.

By practicing these approaches and understanding when each is most effective, you’ll be prepared to solve any system of equations that comes your way.

Graphing and Analyzing Functions

Understanding how to graph and analyze functions is an essential skill in mathematics. The ability to interpret graphical representations allows you to visualize relationships between variables and make predictions based on data. Whether dealing with linear, quadratic, or other types of functions, graphing is a powerful tool for solving problems and identifying patterns.

When graphing a function, the goal is to plot the points that satisfy the equation and form a curve or line. Analyzing the graph involves examining key features, such as the slope, intercepts, and the general shape of the curve. This provides insight into the behavior of the function and helps you understand how changes in one variable affect another.

• Slope: Indicates the steepness of a line and the direction of change between variables.
• Intercepts: The points where the graph crosses the axes, which help determine the function’s values at specific points.
• Vertex: The turning point of a parabola, which represents either the maximum or minimum value of the function.

By mastering graphing techniques and analyzing the resulting graphs, you can gain a deeper understanding of mathematical relationships and apply this knowledge to real-world problems.

Factoring Polynomials Effectively

Factoring polynomials is a crucial skill for simplifying expressions and solving equations. By breaking down complex expressions into simpler factors, you can more easily analyze and manipulate them. Mastering this technique not only enhances problem-solving abilities but also serves as a foundation for more advanced mathematical topics.

Key Methods of Factoring

• Greatest Common Factor (GCF): Start by identifying and factoring out the largest common factor from all terms.
• Factoring by Grouping: Group terms in a way that allows you to factor each group separately, and then factor out the common binomial.
• Difference of Squares: Recognize and apply the formula a² – b² = (a – b)(a + b) to factor expressions of this type.
• Trinomial Factoring: Look for two numbers that multiply to give the product of the first and last terms while adding up to the middle term.

Steps to Successful Factoring

• Identify the type of polynomial and the appropriate factoring method.
• Carefully apply the chosen technique to break down the expression.
• Check your work by multiplying the factors to ensure they result in the original polynomial.

By practicing these methods, you will be able to factor polynomials more efficiently, making it easier to solve complex mathematical problems.

Solving Inequalities with Variables

Solving inequalities involves determining the range of values for a variable that satisfy a given condition. Unlike equations, inequalities express relationships where one side may be greater than or less than the other, rather than equal. Mastering how to solve these expressions is essential for interpreting real-world situations where exact values are not always required, but rather a range of possible outcomes.

When solving inequalities with variables, it is important to apply similar strategies to solving equations, with some key differences, especially when multiplying or dividing by negative numbers. These changes can flip the direction of the inequality sign, which is an essential point to remember during the process.

Basic Steps for Solving Inequalities

• Isolate the variable on one side of the inequality.
• Perform operations like addition, subtraction, multiplication, or division, keeping track of the inequality sign.
• If multiplying or dividing by a negative number, reverse the inequality sign.
• Check the solution by testing values from the solution set.

Common Types of Inequalities

Type	Example	Solution
Linear Inequality	x + 3 > 7	x > 4
Compound Inequality	2	1
Quadratic Inequality	x² – 5x + 6	x ∈ (1, 6)

By understanding these techniques and recognizing different types of inequalities, you’ll be able to solve them confidently and accurately.

Understanding Rational Expressions

Rational expressions are algebraic fractions where both the numerator and the denominator are polynomials. Working with these expressions involves simplifying, multiplying, dividing, and solving equations that include fractions. Understanding the properties of these expressions is essential for solving a variety of mathematical problems, particularly those involving proportional relationships or rates.

To simplify rational expressions, it’s important to identify common factors in both the numerator and denominator. By factoring and canceling out these common factors, the expression becomes easier to work with. Additionally, recognizing restrictions on the domain of the expression is crucial, as certain values for the variable can make the denominator equal to zero, which would make the expression undefined.

Simplifying Rational Expressions

• Factor the numerator and denominator separately.
• Cancel out common factors between the numerator and the denominator.
• Ensure that the simplified expression is in its lowest terms.

Solving Equations with Rational Expressions

• To solve, first eliminate the fractions by multiplying both sides of the equation by the least common denominator (LCD).
• Solve the resulting equation as you would any polynomial equation.
• Check for extraneous solutions, as multiplying by the LCD could introduce values that make the denominator zero.

By practicing the simplification and solving techniques, you’ll become more comfortable working with rational expressions, which are commonly found in many fields like engineering, economics, and physics.

Working with Exponents and Powers

Exponents and powers are mathematical concepts that help in expressing repeated multiplication in a compact form. These tools allow for more efficient calculations, especially when dealing with large numbers or complex expressions. Understanding how to apply the rules of exponents is crucial for simplifying expressions and solving equations efficiently.

When working with exponents, it is important to know the basic laws that govern their operations. These rules allow you to manipulate and simplify expressions involving powers, making calculations easier and faster. Whether multiplying, dividing, or raising a power to another power, mastering these rules will help you handle more advanced mathematical concepts.

Key Exponent Rules

• Product Rule: When multiplying terms with the same base, add the exponents. For example, a^m * a^n = a^(m+n).
• Quotient Rule: When dividing terms with the same base, subtract the exponents. For example, a^m / a^n = a^(m-n).
• Power of a Power: When raising a power to another power, multiply the exponents. For example, (a^m)^n = a^(m*n).
• Zero Exponent: Any non-zero number raised to the power of zero equals one. For example, a^0 = 1.
• Negative Exponent: A negative exponent means the reciprocal of the base raised to the positive exponent. For example, a^(-n) = 1/a^n.

Applying Exponent Rules

• Start by simplifying the base and applying the appropriate exponent rule.
• Rearrange the expression to ensure all terms are in the simplest possible form.
• Check your work by verifying the calculated result through substitution or other methods.

By consistently practicing these rules, you will be able to manipulate powers and exponents with ease, improving your ability to solve a wide range of mathematical problems.

Tips for Word Problems Success

Word problems can often seem challenging because they require translating real-world scenarios into mathematical expressions. However, with the right approach, they can become much easier to tackle. The key is to break down the problem into manageable steps and carefully analyze each part before applying mathematical operations.

Start by carefully reading the problem and identifying the given information and what is being asked. Highlighting key details can help ensure that nothing important is missed. Once you understand the context, set up an equation or expression that reflects the relationships between the variables. Afterward, solve the equation and interpret the solution in the context of the problem.

Steps for Solving Word Problems

• Read the Problem Carefully: Take your time to understand all the details and highlight important numbers or phrases.
• Define Variables: Assign variables to the unknown quantities you’re trying to find.
• Write an Equation: Translate the word problem into a mathematical expression based on the relationships described in the text.
• Solve the Equation: Use the appropriate mathematical techniques to solve for the unknowns.
• Check the Solution: Verify your answer by plugging it back into the context of the problem to ensure it makes sense.

Common Strategies for Word Problems

• Identify Key Words: Words like “sum,” “difference,” “product,” and “quotient” often indicate the type of operation to use.
• Draw Diagrams: For problems involving distances, areas, or geometric shapes, sketching a diagram can help visualize the situation.
• Use Units of Measurement: Pay attention to the units (e.g., miles, hours, money) to ensure consistent measurements throughout the problem.

By following these tips and practicing regularly, you can become more comfortable with word problems and approach them with greater confidence and accuracy.

Important Properties of Algebra

Understanding the foundational properties of mathematical operations is essential for solving a wide variety of problems. These properties provide the rules that govern how numbers and expressions can be manipulated, allowing for simplification and more efficient calculations. Familiarity with these properties helps build a strong base for solving complex equations and tackling more advanced topics.

There are several key properties that apply to operations like addition, subtraction, multiplication, and division. Mastering these properties enables you to transform and simplify expressions, making it easier to find solutions. These rules can also be applied in different combinations to solve a range of problems more effectively.

Commutative, Associative, and Distributive Properties

• Commutative Property: The order of operations does not affect the result of addition or multiplication.
  • a + b = b + a
  • a * b = b * a
• Associative Property: The grouping of numbers does not affect the result of addition or multiplication.
  • (a + b) + c = a + (b + c)
  • (a * b) * c = a * (b * c)
• Distributive Property: Multiplication distributes over addition or subtraction.
  • a * (b + c) = a * b + a * c
  • a * (b – c) = a * b – a * c

Identity and Inverse Properties

• Identity Property: There are specific numbers that do not change the value of another number when used in addition or multiplication.
  • a + 0 = a (Additive Identity)
  • a * 1 = a (Multiplicative Identity)
• Inverse Property: Every number has an opposite or reciprocal that can “cancel out” its effect.
  • a + (-a) = 0 (Additive Inverse)
  • a * (1/a) = 1 (Multiplicative Inverse, for a ≠ 0)

Mastering these properties allows for easier manipulation of expressions and equations, ensuring that problems can be solved in the most efficient way possible. With consistent practice, these properties become second nature, helping you approach more complex mathematical challenges with confidence.

Mastering Absolute Value Equations

Understanding how to solve equations involving absolute values is an important skill in mathematics. These types of equations can often seem tricky at first, but by applying a systematic approach, they become much more manageable. The key to solving absolute value equations is recognizing that the absolute value of a number represents its distance from zero, regardless of whether the number is positive or negative.

When solving these equations, it’s important to remember that the absolute value function yields two possible solutions: one where the expression inside the absolute value is positive, and one where it is negative. This duality means that every equation of this type may have two solutions, one for each case. By breaking the problem into two separate equations, you can easily solve for the unknown variable.

Steps to Solve Absolute Value Equations

• Step 1: Isolate the absolute value expression on one side of the equation. This makes it easier to handle the equation and apply the next steps.
• Step 2: Set up two separate equations: one where the expression inside the absolute value is positive, and another where it is negative.
• Step 3: Solve both equations individually to find the possible values for the unknown variable.
• Step 4: Check the solutions by substituting them back into the original equation to ensure they are correct.

Example Problem

Consider the equation |x – 3| = 5. To solve this:

• First, create two cases:
• Case 1: x – 3 = 5, which simplifies to x = 8.
• Case 2: x – 3 = -5, which simplifies to x = -2.
• So, the solutions are x = 8 and x = -2.

By following these steps and practicing a variety of problems, you’ll become more comfortable with solving absolute value equations and be able to tackle similar challenges with ease.

Using the Distributive Property

The distributive property is a fundamental concept in mathematics that allows you to simplify expressions and solve equations more efficiently. It involves distributing a number or variable across terms inside parentheses. By applying this property, you can expand or simplify expressions that initially appear complicated, making them easier to handle. This property is often used in various mathematical operations, such as simplifying expressions, solving equations, and factoring.

In its simplest form, the distributive property states that for any numbers a, b, and c, the following holds true: a(b + c) = ab + ac. This means that when you multiply a by the sum of b and c, you multiply a by both b and c separately, and then add the results together.

Steps for Using the Distributive Property

• Step 1: Identify the number or variable outside the parentheses and the terms inside the parentheses.
• Step 2: Multiply the outside number by each term inside the parentheses.
• Step 3: Simplify the resulting expression by performing the multiplication.
• Step 4: Combine like terms, if necessary, to further simplify the expression.

Example Problem

Consider the expression 3(x + 4). Using the distributive property:

• Multiply 3 by both x and 4:
• 3 * x = 3x
• 3 * 4 = 12
• The simplified expression is 3x + 12.

Distributive Property with Negative Numbers

When dealing with negative numbers, the distributive property still applies. For example, consider the expression -2(y – 5). Using the distributive property:

Expression	Multiplication Step	Simplified Result
-2(y – 5)	-2 * y = -2y, -2 * -5 = 10	-2y + 10

The simplified expression is -2y + 10.

By mastering the distributive property, you will be able to handle more complex expressions with confidence and ease. This skill is invaluable in solving problems involving polynomials, equations, and more.

Understanding Functions and Relations

In mathematics, relationships between sets of values are explored to understand how different variables interact. These relationships can be represented in various ways, but two of the most important concepts are functions and relations. Understanding the distinction between the two is crucial for solving problems and applying mathematical principles in different scenarios.

A relation refers to any connection or association between two sets of values, where each element in one set is paired with one or more elements in the other. For example, a relation could be represented by a set of ordered pairs, where each pair connects a value from one group to a corresponding value in another group. However, not all relations are functions.

A function is a specific type of relation where each input is associated with exactly one output. In other words, for every element in the domain (the set of inputs), there must be one and only one corresponding element in the range (the set of possible outputs). This restriction makes functions a more structured and predictable form of relationship, which is essential for modeling real-world situations.

Key Characteristics of a Function

• One-to-One Mapping: Each input in the domain corresponds to exactly one output in the range.
• Vertical Line Test: A graphical test to determine if a relation is a function. If any vertical line crosses the graph at more than one point, it is not a function.
• Domain and Range: The set of all possible inputs (domain) and outputs (range) of a function.

Examples of Functions and Relations

Consider the following examples to illustrate the difference between a function and a general relation:

• Example 1: The set of ordered pairs {(1, 2), (2, 3), (3, 4)} represents a function because each input has one unique output.
• Example 2: The set of ordered pairs {(1, 2), (2, 3), (3, 3)} also represents a function, but with repeated outputs for different inputs.
• Example 3: The set {(1, 2), (2, 3), (3, 2), (3, 4)} is not a function because the input “3” has two different outputs (2 and 4).

By mastering the concepts of functions and relations, you will be able to better analyze patterns and relationships in mathematical problems and real-world situations, from basic graphing to more advanced applications. Understanding how to properly classify and interpret these relationships will help improve your problem-solving skills and lead to a deeper comprehension of mathematics.

Preparing with Practice Tests

One of the most effective strategies for reinforcing your understanding and boosting confidence is to practice solving problems under timed conditions. Simulating the experience of working through problems, similar to those you will face, helps identify areas of weakness and provides an opportunity to solidify your knowledge. Practice tests offer an ideal environment to improve both speed and accuracy in solving mathematical challenges.

By engaging with sample problems, you become more familiar with the types of questions that may appear and learn to approach each problem methodically. These exercises also give you insight into the format and structure of questions, allowing you to manage your time more effectively and avoid unnecessary mistakes.

Benefits of Practice Tests

• Improved Problem-Solving Skills: Practicing allows you to refine your methods and strategies for tackling different types of problems.
• Time Management: Completing practice sets within a set time limit helps develop pacing techniques, ensuring you don’t spend too much time on any one question.
• Confidence Boost: Repeated exposure to questions and problem types leads to greater confidence and reduces test anxiety.

How to Maximize Practice Test Results

• Review Mistakes: After completing a practice test, carefully analyze your mistakes. Understanding where you went wrong is key to improving.
• Focus on Weak Areas: Spend extra time on topics that gave you trouble during practice tests to ensure you’re fully prepared.
• Simulate Real Conditions: Try to replicate actual test conditions as closely as possible, including time limits and a distraction-free environment.

Ultimately, consistent practice is key to mastering the material and performing confidently. As you continue to work through practice problems, you’ll not only improve your ability to solve them but also build a deeper understanding of the concepts involved.

Time Management During the Exam

Efficiently managing the available time during a test is essential for maximizing performance. One of the most crucial skills to develop is the ability to allocate your time wisely, ensuring that you can tackle every problem with sufficient focus. Knowing how much time to spend on each question and how to move through the test systematically can prevent unnecessary stress and last-minute rushing.

The key to effective time management is a balance between working quickly and ensuring accuracy. Prioritizing certain sections and leaving more challenging problems for later can help you maintain a steady pace. Additionally, staying aware of the clock and making adjustments to your strategy as needed will give you a better chance of completing all questions within the allotted time.

Effective Time Management Strategies

• Preview the Test: Quickly skim through the entire test before you begin, noting the easier and more challenging sections. This helps you plan where to allocate more time.
• Set Time Limits for Each Section: Divide the available time across sections based on difficulty and the number of questions. Stick to these time limits to avoid spending too much time on any single part.
• Start with the Easy Questions: Begin with the questions you find easiest, building momentum and confidence. This allows you to accumulate quick points and reserve more time for difficult problems.

How to Avoid Time Pressure

• Watch the Clock: Regularly check the time to make sure you’re on track. If you’re spending too long on a question, move on and come back later.
• Skip and Return: If you encounter a difficult question, don’t get stuck. Skip it temporarily and return once you’ve completed the easier questions.
• Stay Calm: If you feel rushed, take a few deep breaths to stay calm. Anxiety can lead to mistakes, so maintaining composure is key to a successful outcome.

By developing these strategies and practicing time management, you’ll be better equipped to perform efficiently, avoid unnecessary stress, and complete the test confidently. Remember, mastering the balance between speed and accuracy can significantly impact your performance on test day.

Common Mistakes to Avoid

When working through problems, certain pitfalls can often lead to incorrect solutions or missed opportunities for points. Being aware of these frequent mistakes is crucial for improving performance and avoiding unnecessary errors. By recognizing where others commonly stumble, you can take proactive steps to avoid them and approach each question with greater precision.

These errors often arise from misinterpreting instructions, skipping over essential steps, or rushing through problems without double-checking work. Developing habits that focus on thoroughness and attention to detail will significantly enhance the accuracy of your solutions.

Frequent Mistakes to Watch Out For

• Misreading the Problem: It’s easy to overlook key details or misinterpret what is being asked. Always take the time to read each question carefully and underline or highlight important information.
• Skipping Steps: Jumping ahead without showing all the steps can lead to errors, even if the final answer looks correct. Always write out each step to ensure logical consistency and make it easier to catch mistakes.
• Not Checking Work: Failing to review answers is a common mistake. Even if you’re confident, take a few minutes at the end to check your calculations and final answers.

How to Prevent These Mistakes

• Take Your Time: Rushing can lead to overlooking small details. Manage your time, but also give yourself a moment to review each question thoroughly before answering.
• Double-Check Key Steps: Ensure each part of the problem has been addressed correctly before moving on. This is especially important in multi-step questions.
• Stay Organized: Write your work neatly and systematically. Disorganized notes can confuse you and lead to mistakes that could have been easily avoided.

By staying mindful of these common mistakes and incorporating these preventative strategies into your problem-solving approach, you can reduce the risk of errors and improve your overall performance. Remember, careful preparation and attention to detail are key to success.