Geometry Final Exam Review Answer Key

Mastering the fundamentals of geometry requires a deep understanding of various concepts and techniques. As you approach your upcoming assessment, it’s essential to reinforce your knowledge and familiarize yourself with the most commonly tested topics. With the right approach, you can boost your confidence and enhance your ability to solve even the most complex problems.

Throughout this section, we will explore critical areas that are often highlighted in assessments, providing a structured path for reinforcing your skills. Whether it’s learning key formulas, practicing problem-solving strategies, or mastering essential principles, this guide will help ensure you’re fully prepared for any challenge that comes your way.

Focus on comprehension and consistent practice is key to achieving success. By the end of this guide, you’ll have a clear roadmap for tackling questions efficiently and confidently, setting yourself up for a strong performance.

Geometry Final Exam Review Answer Key

Achieving success in a mathematics assessment requires a clear understanding of the topics that are frequently tested. A strong foundation in problem-solving, critical thinking, and application of principles can significantly improve performance. This section will provide insights into effective strategies and methods for solving the types of problems often encountered in these types of evaluations.

Understanding Key Principles and Techniques

One of the most important steps in preparing for any math-based assessment is mastering essential principles. These core concepts form the backbone of most questions and help you navigate through more complex problems with ease. Familiarizing yourself with the most frequently tested topics ensures you’re well-equipped for success.

Effective Problem Solving Strategies

Successful problem-solving goes beyond simply memorizing formulas. It involves developing a strategic approach to each question, from understanding the problem to applying the right techniques. Practicing different types of problems will allow you to identify patterns and common approaches, ensuring you can tackle challenges efficiently under pressure.

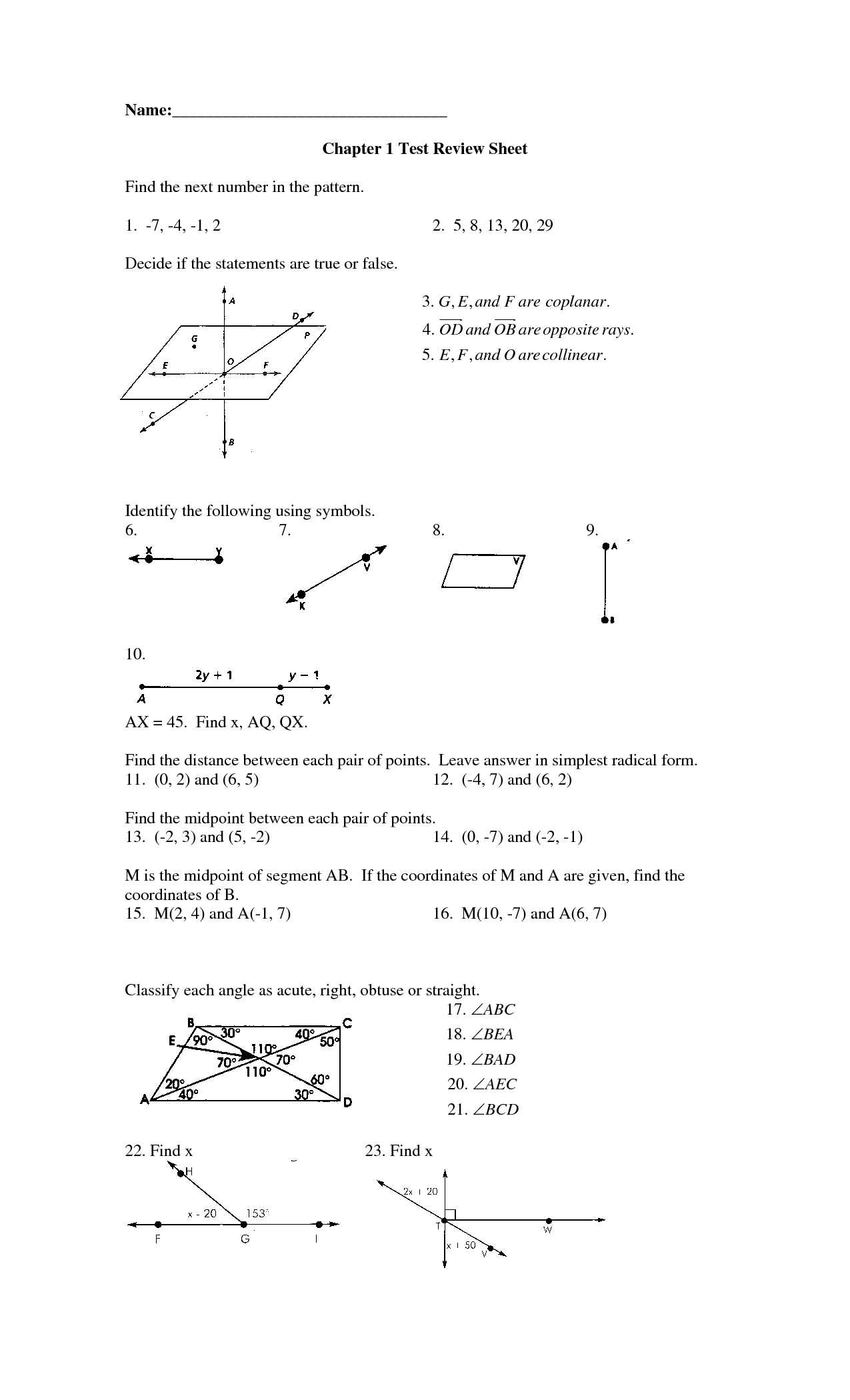
Practice and consistency are crucial to strengthening your abilities. With a solid grasp of core topics and a methodical approach to problem solving, you can approach any challenge with confidence.

Understanding Key Concepts for Success

To excel in any mathematical assessment, it’s essential to have a solid understanding of the core principles that form the foundation of most questions. These fundamental ideas are not just theoretical knowledge but practical tools that allow you to solve problems accurately and efficiently. Recognizing the most important concepts will help you approach any challenge with clarity and confidence.

Mastering these foundational elements enables you to tackle more complex problems with ease. It’s not enough to memorize formulas or steps; comprehension and the ability to apply concepts in different contexts is what sets top performers apart. By focusing on the essentials, you build the confidence needed to face any problem, no matter how challenging.

Essential Formulas to Remember

In any mathematical challenge, having a set of key formulas at your fingertips can make a significant difference in solving problems quickly and accurately. These formulas are the building blocks for a variety of calculations and problem-solving techniques. By understanding and memorizing the most commonly used equations, you can approach even the most complex tasks with greater ease and efficiency.

Basic Geometric Relationships

Some of the most frequently applied formulas are related to basic shapes and their properties. For example, knowing how to calculate the area and perimeter of common polygons, such as triangles, squares, and circles, is essential for solving many questions. Each of these formulas is straightforward but crucial for accurate results.

Volume and Surface Area Calculations

In addition to two-dimensional shapes, understanding how to compute the volume and surface area of three-dimensional objects is key. Formulas for spheres, cylinders, and cones often appear in various problem types, and familiarity with them ensures you can handle these more advanced questions effectively.

Top Strategies for Geometry Exam Prep

Preparing for a mathematical assessment involves more than just understanding the material; it requires strategic planning and focused practice. By utilizing the right techniques, you can significantly improve your problem-solving abilities and boost your performance. These strategies help you not only memorize key concepts but also apply them effectively under time pressure.

Structured Study Plan

Creating a detailed study plan ensures that you cover all necessary topics while leaving enough time for practice and revision. Prioritize areas where you’re weakest, but don’t neglect to review the concepts you’re confident with. This balanced approach helps reinforce your strengths while addressing any gaps in your knowledge.

Practice with Real Problems

One of the best ways to prepare is by solving practice problems that closely resemble the types of questions you’ll encounter. This allows you to develop familiarity with the format and helps you improve your speed and accuracy. Working through different problem sets also helps solidify your understanding of formulas and strategies.

Strategy	Benefit
Timed Practice	Improves speed and time management
Focus on Weak Areas	Addresses gaps in understanding
Review Mistakes	Identifies patterns and common errors

Common Geometry Mistakes to Avoid

Even the most prepared individuals can make simple errors during mathematical assessments. These mistakes, though often minor, can have a significant impact on your overall performance. By recognizing and addressing common pitfalls, you can avoid losing valuable points and improve your problem-solving accuracy.

Misunderstanding Problem Instructions

One of the most frequent mistakes occurs when students fail to fully read or misinterpret the instructions. It’s crucial to understand what each question is asking before diving into calculations. Skipping important details, such as units of measurement or specific conditions in the problem, can lead to incorrect solutions.

Forgetting to Check for Special Conditions

Mathematical problems often come with specific constraints or assumptions. For example, in certain problems, figures might be drawn to scale, or certain angles may be congruent without explicitly stating it. Overlooking these conditions can lead to unnecessary confusion and errors in calculations.

How to Tackle Word Problems Effectively

Word problems often seem challenging because they require translating real-world situations into mathematical equations. However, with a structured approach, these problems can be solved efficiently. By breaking down the information and organizing your thoughts, you can simplify even the most complex scenarios and find the correct solution.

Read and Identify Key Information

Start by carefully reading the problem to understand the context and what is being asked. Highlight or underline key details such as quantities, relationships, and any specific conditions given. This helps you focus on the important elements that need to be included in your equation or calculation.

Translate the Words into Mathematical Expressions

Once you’ve identified the key information, the next step is to translate it into a mathematical form. This might involve converting words into numbers, identifying unknowns, and choosing the right formulas to apply. Clear and logical translation is essential for solving the problem accurately.

Reviewing Geometric Proofs and Theorems

Understanding the principles behind mathematical proofs and theorems is vital for tackling more complex problems. These logical arguments form the foundation for many of the concepts you’ll encounter, and mastering them allows you to demonstrate the validity of relationships between different shapes and figures. This section will guide you through the most important proofs and theorems, ensuring you’re prepared to apply them effectively.

Key Theorems to Remember

Several theorems are frequently used to solve a variety of problems. For instance, the Pythagorean theorem, properties of parallel lines, and the triangle congruence postulates are essential tools for deriving solutions. These theorems not only provide a structured way of approaching problems but also enable you to make logical conclusions based on known facts.

Proof Strategies and Approaches

When faced with a proof, it’s important to follow a clear and methodical approach. Start by stating the given information and what needs to be proven. Then, use logical steps, incorporating relevant theorems and properties, to connect the given facts to the desired conclusion. Practicing different types of proofs will help strengthen your reasoning skills and improve your ability to tackle complex challenges.

Mastering Coordinate Geometry for the Exam

Coordinate geometry is a powerful tool that connects algebra and geometry through the use of graphs and equations. By mastering this area, you can solve a variety of problems related to points, lines, and shapes on a coordinate plane. Understanding how to apply formulas and interpret geometric relationships in a coordinate system is essential for tackling these types of questions effectively.

To succeed in this area, focus on key concepts such as the distance formula, midpoint formula, and slope calculations. These are the building blocks that allow you to analyze the positions and relationships between geometric figures on a graph. With consistent practice and a strong grasp of these concepts, you will be well-prepared to approach coordinate-based problems with confidence and precision.

Essential Geometry Graphing Techniques

Graphing is an indispensable skill that allows you to visualize and solve problems involving points, lines, and shapes. Whether you’re dealing with linear equations, geometric figures, or transformations, the ability to plot and interpret graphs is key to solving many types of questions. In this section, we’ll focus on the essential techniques that will help you accurately represent and analyze various mathematical concepts on a coordinate plane.

Plotting Points and Lines

Accurate plotting is the foundation of graphing. Begin by marking key points on the plane using their respective coordinates. Once points are plotted, you can connect them to form lines or curves. Understanding how to calculate and graph the slope of a line, as well as how to interpret the y-intercept, is essential for solving many problems. Practice plotting both vertical and horizontal lines, as well as diagonal ones, to become comfortable with different slopes.

Graphing Transformations

Graphing transformations, such as translations, rotations, reflections, and dilations, is crucial for understanding the movement and changes in figures on a coordinate plane. Each type of transformation follows specific rules, and mastering these can help you solve problems that involve changing the position or size of geometric shapes. Knowing how to apply these transformations to both points and shapes will enhance your ability to visualize and solve related problems effectively.

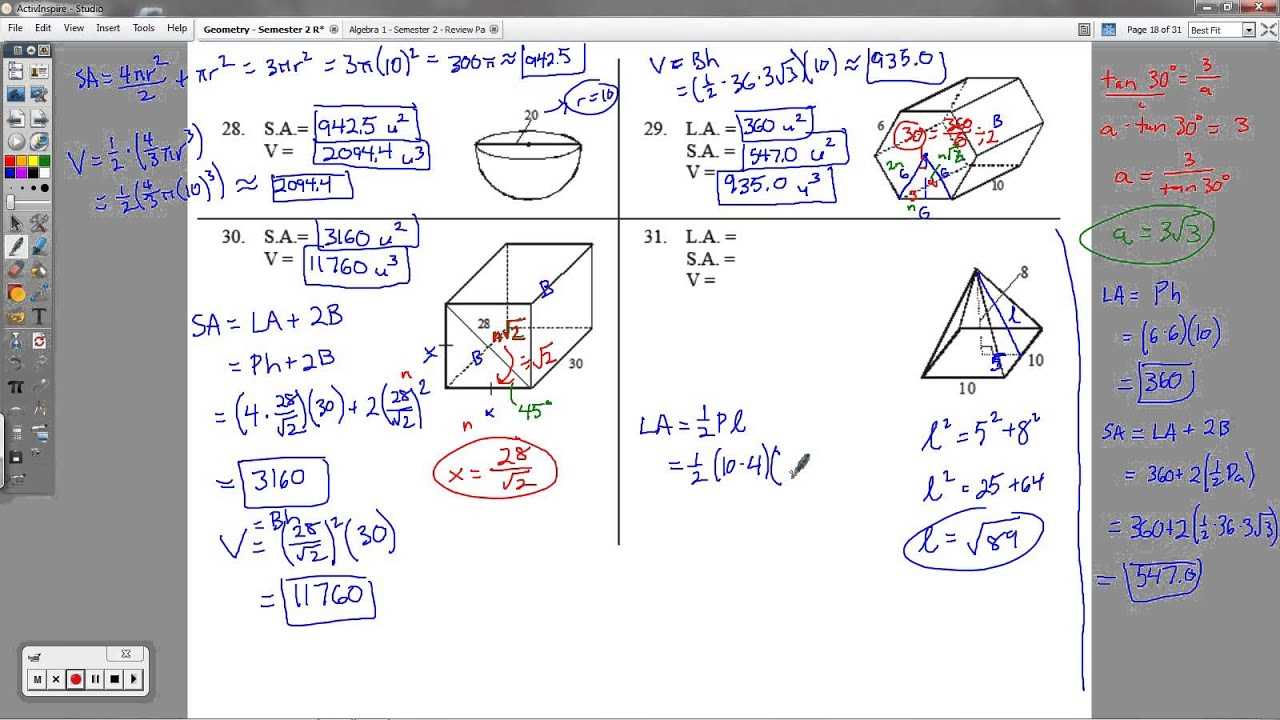
Area and Volume Formulas You Need

Understanding how to calculate areas and volumes is essential for solving problems involving two-dimensional and three-dimensional shapes. Whether you’re working with simple polygons or more complex solids, having the right formulas at your disposal can make all the difference. In this section, we’ll cover the key formulas you need to know, helping you confidently tackle a wide range of problems.

Area Formulas

There are several formulas for calculating the area of common shapes. Here are the most frequently used ones:

• Rectangle: Area = length × width
• Square: Area = side²
• Triangle: Area = ½ × base × height
• Circle: Area = π × radius²
• Parallelogram: Area = base × height

Volume Formulas

For three-dimensional shapes, volume formulas are crucial to understanding the capacity of solids. Here are some of the most important volume formulas:

• Rectangular Prism (Cuboid): Volume = length × width × height
• Cube: Volume = side³
• Cylinder: Volume = π × radius² × height
• Sphere: Volume = (4/3) × π × radius³
• Pyramid: Volume = (1/3) × base area × height
• Cone: Volume = (1/3) × π × radius² × height

By mastering these formulas and understanding how to apply them, you’ll be well-equipped to solve problems related to both surface area and volume. Be sure to practice using these formulas in various scenarios to reinforce your understanding.

Practical Tips for Geometry Problem Solving

When solving mathematical problems involving shapes, measurements, and spatial relationships, having a strategic approach is key. The right techniques can help you break down complex questions into manageable parts and find the solution more efficiently. In this section, we’ll share some practical tips to improve your problem-solving skills and boost your confidence in tackling these types of challenges.

Step-by-Step Approach

One of the most effective ways to approach a problem is by following a clear, logical process. Begin by reading the problem carefully and identifying all the relevant information. Draw a diagram if necessary to visualize the situation. Next, organize the given data and think about which concepts or formulas apply. Break down the steps required to reach a solution, and proceed systematically to avoid confusion or mistakes.

Practice with Different Types of Problems

Exposure to a wide variety of problems helps build your problem-solving skills. Practice different types of questions that involve various shapes, theorems, and techniques. This will allow you to recognize patterns and become familiar with the strategies that work best for different problem types. The more you practice, the faster and more accurate you will become at solving similar problems in the future.

Practice Questions with Solutions

Working through practice problems is one of the best ways to sharpen your skills and prepare for assessments. In this section, we will provide a series of practice questions that cover various aspects of mathematical reasoning involving shapes, measurements, and spatial relationships. Each question will be followed by a detailed solution to help you understand the process and steps involved in finding the correct answer.

Practice Problems

Below are some sample problems to test your understanding:

• Problem 1: Find the area of a triangle with a base of 10 units and a height of 6 units.
• Problem 2: A rectangle has a length of 8 units and a width of 5 units. What is its perimeter?
• Problem 3: Calculate the volume of a cylinder with a radius of 4 units and a height of 10 units.
• Problem 4: A circle has a radius of 7 units. What is its circumference?

Solutions

Here are the solutions to the above problems:

1. Solution to Problem 1: Area = ½ × base × height = ½ × 10 × 6 = 30 square units.
2. Solution to Problem 2: Perimeter = 2 × (length + width) = 2 × (8 + 5) = 26 units.
3. Solution to Problem 3: Volume = π × radius² × height = π × 4² × 10 ≈ 502.65 cubic units.
4. Solution to Problem 4: Circumference = 2 × π × radius ≈ 2 × π × 7 ≈ 43.98 units.

By working through these examples, you can become more familiar with applying formulas and solving problems in a systematic way. Practicing regularly will help reinforce your understanding and prepare you for more complex challenges.

Key Trigonometry Concepts in Geometry

Trigonometry plays a crucial role in understanding the relationships between angles and sides in various shapes, especially when dealing with right-angled structures. This section explores essential trigonometric concepts that are frequently used in solving problems involving angles, lengths, and other geometric properties. Understanding these concepts is vital for mastering various calculations and geometric proofs.

Sine, Cosine, and Tangent

One of the foundational ideas in trigonometry involves the ratios of the sides of a right triangle. These ratios are expressed through sine, cosine, and tangent functions. The sine of an angle is the ratio of the length of the opposite side to the hypotenuse, cosine is the ratio of the adjacent side to the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side. These functions are used to find missing angles and side lengths in right triangles.

The Pythagorean Theorem

The Pythagorean theorem is another key concept in trigonometry that applies to right triangles. It states that the square of the length of the hypotenuse is equal to the sum of the squares of the other two sides. This relationship helps in determining missing side lengths when two sides are known. The formula is expressed as:

a² + b² = c², where a and b are the lengths of the two legs, and c is the length of the hypotenuse.

By mastering these basic trigonometric functions and formulas, you will be able to tackle a wide range of geometric problems involving angles, distances, and various other spatial relationships.

How to Manage Time During the Test

Effective time management is essential for success in any test. Without a clear strategy, it can be easy to run out of time, especially when facing a variety of problems. To maximize your performance, it is crucial to plan your approach, prioritize tasks, and maintain focus throughout the entire process. This section provides strategies to help you manage your time effectively, ensuring you complete the test efficiently and accurately.

Start by allocating a set amount of time to each section based on its difficulty and the number of questions. Begin with easier problems to build confidence and save more time for complex ones. Keep an eye on the clock, but avoid focusing on it too much, as this can cause unnecessary stress. If you get stuck on a question, move on and return to it later if time permits. This prevents you from wasting time on one problem when others may be easier or quicker to solve.

By following these techniques, you can ensure that you make the most of your allotted time and approach each task with a clear, focused mindset.

Effective Study Methods for Geometry

Mastering mathematical concepts requires a focused and systematic approach to studying. When preparing for tests involving spatial reasoning, angles, and measurements, it’s essential to use study methods that reinforce both understanding and application of concepts. This section explores several strategies to help you succeed in mastering these topics and performing well on assessments.

Utilizing Practice Problems

One of the most effective ways to improve your skills is by solving a wide range of practice questions. Repetition helps solidify understanding and exposes you to different problem types. Here are some techniques for making the most out of practice:

• Start with simpler problems to build confidence and gradually move on to more challenging ones.
• Identify areas where you struggle and dedicate extra time to those concepts.
• Track your progress and review mistakes to understand the reasoning behind them.

Study Groups and Collaboration

Collaborating with peers can enhance your understanding. Explaining difficult concepts to others can solidify your own knowledge. Consider these tips for effective study groups:

• Work together to break down complex topics into manageable pieces.
• Ask each other questions and encourage open discussion of problem-solving techniques.
• Practice explaining solutions clearly and logically to improve your communication skills.

By incorporating these study strategies, you can build a deeper understanding of the material and prepare yourself for success on the test day.

How to Handle Test Anxiety

Feeling nervous or anxious before an important assessment is a common experience for many students. These emotions can sometimes hinder your ability to perform at your best. Learning how to manage test anxiety is crucial for maintaining focus and confidence during the assessment process. By adopting certain strategies, you can transform nervous energy into a productive mindset that helps you excel.

Preparation is Key

One of the most effective ways to reduce anxiety is thorough preparation. When you feel confident about the material, you’re less likely to be overwhelmed during the test. Here are some strategies to prepare yourself:

• Practice consistently, focusing on weak areas to boost confidence.
• Establish a routine leading up to the assessment to help manage time effectively.
• Simulate real test conditions by setting a timer and solving practice problems within a set timeframe.

Relaxation Techniques

While preparation helps build confidence, managing your stress levels on the day of the test is equally important. Here are some methods to reduce anxiety and stay calm:

Relaxation Method	How It Helps
Deep Breathing	Slows down your heart rate and calms the nervous system.
Visualization	Helps create a mental image of success, boosting your confidence.
Progressive Muscle Relaxation	Releases physical tension, reducing stress and promoting focus.

Incorporating these techniques before and during the test can help you manage anxiety, allowing you to stay focused and perform at your best.

Resources for Further Practice

To master the concepts covered in this subject, it’s important to continuously practice and reinforce your understanding. Various resources can provide additional exercises, explanations, and interactive tools to help you improve your skills. Whether you prefer structured lessons, self-paced practice, or interactive platforms, there are plenty of options to choose from.

Online Learning Platforms

Several online platforms offer comprehensive tutorials and practice problems to help you deepen your understanding. These resources often provide step-by-step guides and real-time feedback to help you track your progress. Consider exploring the following:

• Khan Academy: Offers free video lessons, practice exercises, and quizzes on a variety of topics.
• Coursera: Provides access to specialized courses from top universities, with interactive assignments.
• EdX: Features free and paid courses, including many that offer self-paced learning options.

Books and Workbooks

If you prefer a more traditional approach, books and workbooks can be invaluable for self-study. Many books are tailored for students at different skill levels, and include a wide range of problems for practice. Look for resources such as:

• “How to Solve It” by George Pólya: A classic that offers strategies for approaching mathematical problems.
• Practice Workbooks: Look for titles from publishers like Barron’s or the Princeton Review, which often offer targeted problem sets with solutions.

By using these resources, you can continue building and strengthening your knowledge, ensuring that you are well-prepared for any challenge that comes your way.