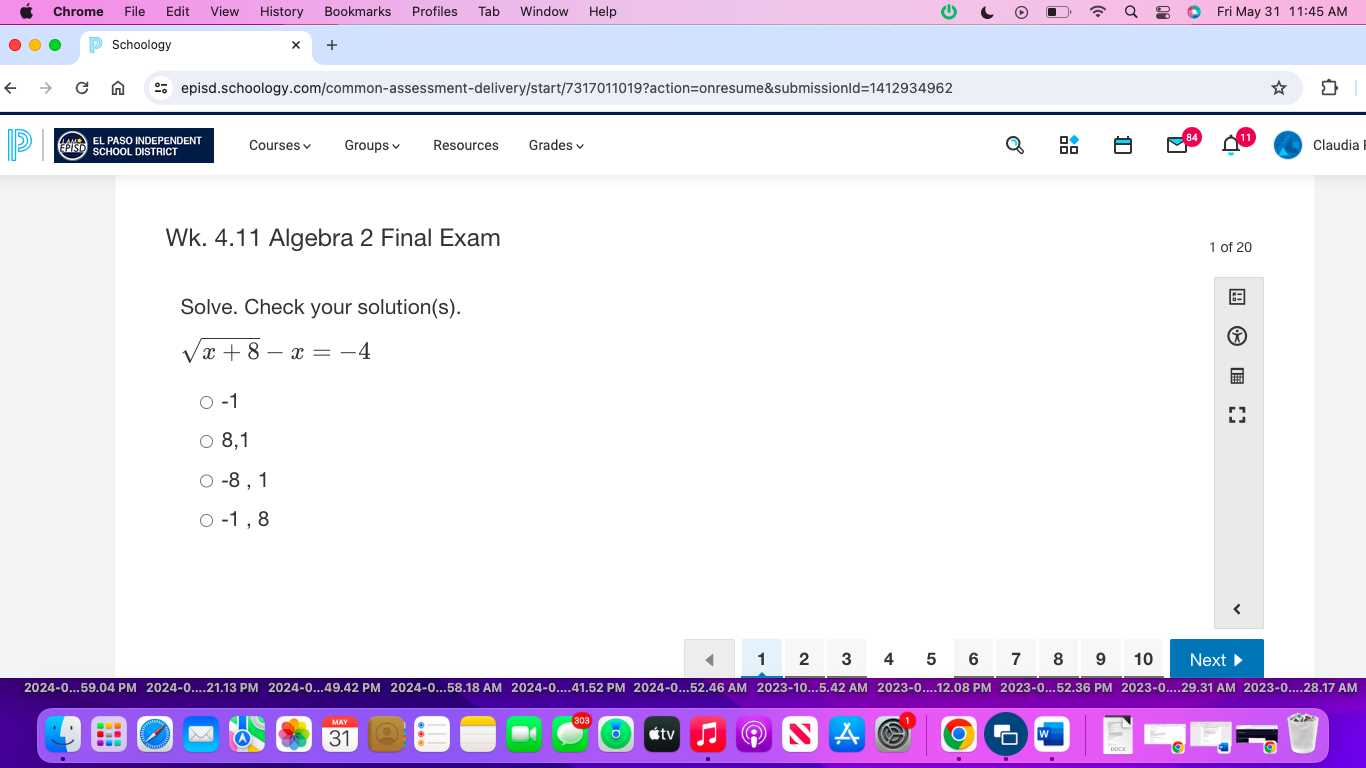
Algebra 2 Final Exam Answers and Solutions

As you prepare to face the challenges of an advanced mathematics assessment, understanding key principles and mastering problem-solving strategies is essential. This process involves not only reviewing theoretical concepts but also applying them in practical scenarios. The key to performing well lies in consistent practice and the ability to think critically about each problem.

Building a solid foundation will help you tackle even the most complex questions with confidence. Being familiar with the underlying methods and recognizing patterns can significantly reduce the time spent on each task. It’s important to approach each problem strategically, breaking it down into manageable steps.

Through effective preparation, you’ll be able to navigate through a variety of question types, from basic calculations to more intricate multi-step problems. Confidence comes from familiarity, and thorough practice ensures you can recall necessary formulas and techniques when needed.

Algebra 2 Final Exam Preparation Tips

Preparing for an important math assessment requires a strategic approach to ensure you understand the material and can apply concepts effectively. Effective preparation involves more than just reviewing notes; it requires practicing problem-solving techniques, identifying common question types, and focusing on areas where you may need additional practice. Building confidence through consistent practice can help reduce stress and increase performance.

Focus on Key Concepts

Identify the core topics that are most likely to appear during the assessment. Concentrate on understanding the underlying principles behind each problem type rather than memorizing formulas. Mastering the foundational concepts will allow you to approach any question with a clear strategy. Practice a variety of problems to become familiar with different ways questions can be framed.

Use Practice Tests

One of the most effective methods of preparing is simulating test conditions. Take timed practice tests to assess your readiness. This will not only help you become more comfortable with the format but also improve your time management. Analyze your performance after each test to pinpoint areas for improvement and adjust your study plan accordingly.

Understanding Key Algebra 2 Concepts

Mastering the essential mathematical principles is crucial for success in any assessment. Focus on grasping the core ideas that underpin a wide range of problems. This includes learning how to manipulate expressions, solve equations, and understand functions, all of which are central to solving more complex questions. A deep understanding of these core concepts helps build confidence and ensures you can approach challenges methodically.

Key areas to focus on include simplifying polynomials, solving systems of equations, and working with different types of functions such as quadratic and exponential. Each of these topics plays a significant role in solving more intricate problems. Familiarity with their structure will make it easier to recognize patterns and apply the right strategies when needed.

How to Tackle Exam Questions Effectively

Approaching assessment questions with a clear strategy is essential for achieving the best results. The key to success lies in staying organized, managing time efficiently, and applying the right problem-solving techniques. By breaking down complex tasks into smaller, manageable steps, you can reduce the likelihood of errors and ensure that you answer each question accurately.

Read Each Question Carefully

Before jumping into solving a problem, take a moment to read it thoroughly. Understanding what is being asked is the first step towards finding the correct solution. Pay attention to key terms and phrases that indicate the operation needed, whether it’s simplifying an expression, solving for a variable, or graphing a function. Highlight important details to ensure that no part of the question is overlooked.

Break Down Complex Problems

If you encounter a challenging problem, break it into smaller steps. Start by identifying what is given and what is being asked for. This approach makes it easier to focus on solving one part at a time. Check your progress as you go along, ensuring that each step logically follows from the last, and review your calculations before finalizing your answer.

Common Mistakes to Avoid in Algebra 2

When working through complex mathematical problems, it’s easy to make simple mistakes that can cost valuable points. Being aware of common pitfalls can help you avoid them and improve your overall performance. Focus on understanding the process behind each calculation, and remember that attention to detail is key. By recognizing typical errors, you can correct them before they become habits.

Common Mistake	How to Avoid It
Misinterpreting the Problem	Read the question carefully, highlighting key terms and operations to ensure you understand the requirements.
Skipping Steps in Calculation	Work through each step systematically and double-check your work as you go along.
Forgetting to Simplify	Always simplify expressions before moving to the next step to avoid unnecessary complexity.
Incorrectly Applying Formulas	Familiarize yourself with formulas and make sure to apply them correctly in the right context.
Not Checking for Errors	Review your answers before submitting, checking for common mistakes such as sign errors or miscalculations.

Top Study Resources for Algebra 2

Utilizing a variety of study resources can enhance your understanding of key concepts and improve your problem-solving skills. The right tools allow you to practice different types of questions, reinforce learning, and clarify any areas of confusion. Here are some of the most effective study materials that can help you succeed.

• Online Tutorials: Websites such as Khan Academy and Coursera offer free lessons and practice exercises that cover essential topics. These platforms often break down complex problems into simpler steps, making it easier to grasp challenging concepts.
• Textbooks and Practice Books: Comprehensive textbooks often provide in-depth explanations and examples for each topic. Practice books are particularly useful for honing skills with a wide variety of problems, giving you an opportunity to apply what you’ve learned.
• Study Apps: Apps like Photomath and Wolfram Alpha allow you to input problems and receive step-by-step solutions. These tools can serve as both a learning aid and a way to check your work.
• Flashcards: Create flashcards for key formulas, rules, and concepts. These can be an excellent way to quickly review and reinforce information while studying on the go.
• Video Lessons: YouTube channels dedicated to mathematics education, such as PatrickJMT and Professor Leonard, offer detailed video explanations for various topics, helping visual learners understand the material more clearly.

By combining these resources, you can strengthen your skills, clarify misunderstandings, and prepare effectively for any challenge you may face.

Breaking Down Complex Algebra Problems

When faced with a challenging problem, breaking it down into smaller, more manageable parts is essential. This method allows you to focus on one step at a time, reducing the risk of errors and increasing your chances of success. By understanding the structure of the problem and addressing each element separately, you can solve even the most complex questions with confidence.

Identify the Key Information

The first step in tackling a difficult problem is to extract the essential details. Carefully read through the question, underlining important terms and numbers. Knowing exactly what is being asked will guide you through the necessary steps and prevent you from getting sidetracked by irrelevant information.

Break the Problem Into Steps

Once you’ve identified the key elements, divide the problem into smaller parts. Start by addressing the simplest operation and work your way through each step methodically. Whether it involves simplifying expressions, solving for variables, or graphing, taking it step by step ensures that you don’t miss crucial steps along the way. Recheck each step before moving forward to confirm your calculations are accurate.

Time Management Strategies for the Exam

Effectively managing your time during an assessment is crucial to ensure you have enough time to tackle every problem without feeling rushed. Developing a clear plan before and during the test will help you allocate time efficiently, allowing you to complete each question thoughtfully and thoroughly. The goal is to work at a steady pace while avoiding spending too much time on any single problem.

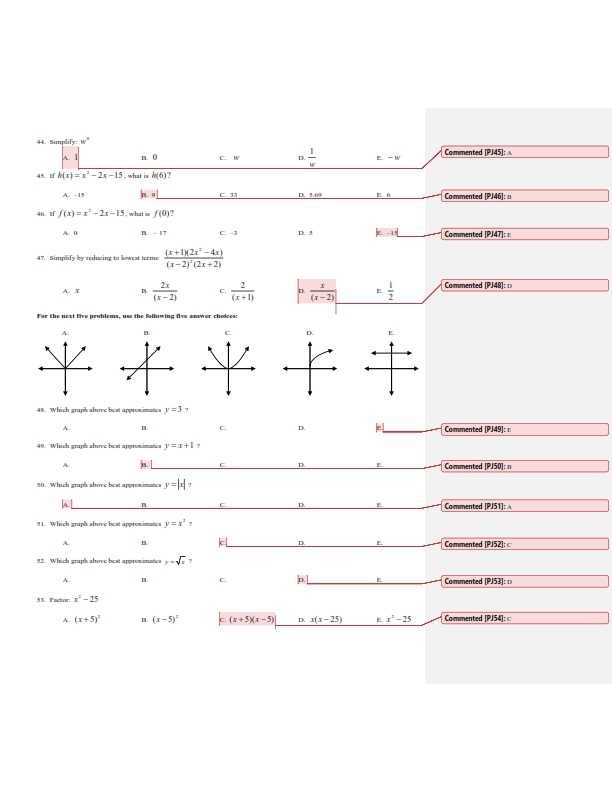
Start by quickly scanning the entire test to get an overview of the questions. This allows you to allocate time based on the difficulty of each section. If a question seems too complex, move on to others and return to it later when you have more time. Another effective strategy is to set a time limit for each section and stick to it, ensuring that you’re not dedicating too much time to any one task. Prioritize easier questions to build confidence and gain quick points before tackling more challenging problems.

Mastering Quadratic Equations for Success

Quadratic equations are a fundamental topic that often appears in assessments, and mastering them is key to achieving success. Understanding the different methods for solving these equations can help you approach a wide variety of problems with confidence. By focusing on the core strategies and practicing regularly, you can significantly improve your ability to solve these problems quickly and accurately.

The most common techniques for solving quadratic equations include factoring, using the quadratic formula, and completing the square. Each method has its strengths, depending on the specific problem at hand. Mastering these techniques allows you to choose the best approach based on the equation you’re facing. Regular practice will help you recognize patterns and improve your speed, which is essential for completing problems efficiently.

Additionally, understanding the relationship between the equation’s coefficients and its graph can provide valuable insight into the problem-solving process. With time and practice, you’ll be able to approach quadratic equations with greater ease, leading to improved performance in your studies.

How to Use the Formula Sheet Wisely

A formula sheet can be a valuable tool during an assessment, providing quick access to essential equations and methods. However, it’s important to use it wisely to maximize its effectiveness. Relying too heavily on the formula sheet without understanding the underlying concepts can lead to mistakes. Instead, the formula sheet should be used as a reference to support your problem-solving process, not as a crutch.

Before the test, familiarize yourself with the layout of the formula sheet. Knowing where each equation is located allows you to quickly find what you need during the assessment. Practice applying formulas in different scenarios so that you don’t have to spend time looking them up during the test. This approach will also help you become more comfortable with how to use the formulas correctly in context.

Additionally, avoid memorizing formulas without understanding them. Knowing how each equation is derived or when it should be used gives you a deeper understanding of the material and prevents reliance on the sheet in stressful moments. Effective use of the formula sheet is about reinforcing your knowledge, not substituting for it.

Graphing Techniques for Algebra 2 Tests

Graphing is an essential skill in many mathematical assessments, and mastering different graphing techniques can greatly improve your performance. Whether you’re working with linear, quadratic, or exponential equations, having a clear strategy for plotting points and interpreting graphs is crucial. Understanding how to visualize equations on a coordinate plane helps you grasp complex concepts and solve problems more efficiently.

Essential Graphing Strategies

• Plotting Points Accurately: Always start by plotting key points on the graph. Identify the x- and y-intercepts, and mark them clearly. This gives you a solid foundation to draw the graph.
• Using the Slope-Intercept Form: When graphing linear equations, the slope-intercept form (y = mx + b) can make the process easier. Start with the y-intercept and use the slope to find other points.
• Identifying Key Features of Parabolas: For quadratic equations, focus on the vertex, axis of symmetry, and direction of opening. This helps you sketch the curve accurately without needing to plot many points.

Tips for Efficient Graphing

• Use a Table of Values: When graphing more complex functions, creating a table of values can help you generate accurate points to plot on the graph.
• Look for Symmetry: Many functions, especially quadratics and absolute value functions, have symmetry. Recognizing this can save time and help you sketch the graph more efficiently.
• Check the Scale: Make sure that your graph is scaled correctly to avoid distorting the shape of the function. A consistent scale helps in interpreting the graph accurately.

By practicing these techniques and familiarizing yourself with different types of functions, you can graph equations quickly and accurately, improving your performance in any mathematical assessment.

Solving Systems of Equations Quickly

Solving systems of equations efficiently is an essential skill that can save you time during any assessment. By using the right methods and strategies, you can quickly find solutions without getting bogged down by complex calculations. Understanding various approaches will help you decide which technique is best for each situation, allowing you to solve problems faster and more accurately.

Effective Methods for Solving Systems

• Substitution Method: If one equation is already solved for one variable, substitute this expression into the other equation. This allows you to reduce the system to a single equation with one variable, making it easier to solve.
• Elimination Method: Add or subtract equations to eliminate one variable, leaving you with a simpler equation. Once you solve for the remaining variable, substitute the value back into one of the original equations to find the other variable.
• Graphing Method: If the equations are simple and can be easily graphed, plotting both equations on the same coordinate plane can quickly show where the lines intersect. The point of intersection is the solution to the system.

Tips for Speed and Accuracy

• Check for Easy Substitutions: Look for opportunities to substitute or eliminate variables early. If one equation is already simplified or if a variable has a coefficient of 1 or -1, use it to simplify your work.
• Multiply to Eliminate: If the coefficients of one variable aren’t the same, multiply one or both equations by appropriate factors to match the coefficients. This will make it easier to eliminate that variable.
• Double-Check Your Work: After finding the solution, substitute the values back into the original equations to ensure they satisfy both equations. This helps avoid errors, especially in multi-step problems.

By mastering these methods and practicing regularly, you can approach systems of equations confidently and solve them in a fraction of the time. This will improve both your speed and accuracy during assessments.

Understanding Exponents and Polynomials

Mastering exponents and polynomials is crucial for solving many advanced problems in mathematics. These concepts form the foundation for more complex operations, including simplifying expressions, solving equations, and analyzing functions. By understanding how to work with exponents and polynomials, you can efficiently manipulate algebraic expressions and solve a wide variety of problems with ease.

Key Concepts in Exponents

• Product Rule: When multiplying terms with the same base, add their exponents. For example, x^a * x^b = x^(a + b).
• Power of a Power Rule: When raising a power to another power, multiply the exponents. For example, (x^a)^b = x^(a * b).
• Negative Exponents: Negative exponents represent the reciprocal of the base raised to the opposite positive exponent. For example, x^(-a) = 1/x^a.

Working with Polynomials

Polynomials are expressions made up of terms that include variables raised to non-negative integer powers, along with their coefficients. Understanding how to add, subtract, and multiply polynomials is essential for simplifying and solving complex algebraic expressions.

Operation	Example	Result
Addition	(2x^2 + 3x) + (4x^2 – x)	6x^2 + 2x
Subtraction	(5x^3 + 2x) – (3x^3 + x)	2x^3 + x
Multiplication	(x + 2)(x – 3)	x^2 – x – 6

By practicing these rules and operations, you’ll be able to simplify complex expressions and solve problems efficiently. A strong understanding of exponents and polynomials is essential for success in advanced mathematical topics and assessments.

Practical Applications of Algebra 2 Knowledge

The concepts learned in this area of study are not just academic–they have real-world applications in a variety of fields. Mastery of these ideas can provide valuable tools for solving everyday problems, making informed decisions, and advancing in technical or scientific careers. Understanding how to manipulate equations, work with functions, and analyze data can open doors to numerous opportunities, both in higher education and in the workforce.

One of the key areas where this knowledge is applied is in engineering and technology. Engineers use mathematical principles to design structures, analyze systems, and solve real-world problems. Whether it’s determining the best materials for a project or calculating the optimal angles for a bridge, the ability to work with mathematical models is indispensable. Additionally, data scientists and software developers rely on similar principles when working with algorithms or creating simulations.

Moreover, business professionals use these concepts in financial modeling, analyzing profit and loss, and even in marketing strategies. Calculating growth rates, analyzing trends, and making predictions all rely on the mathematical principles taught in this discipline. For instance, understanding functions and their behaviors helps in making sense of how markets react over time, enabling businesses to make informed predictions about future performance.

In healthcare and biology, these concepts help with data analysis and modeling. Whether it’s determining the spread of a disease, calculating medication dosages, or even analyzing patient data, the ability to apply mathematical techniques is critical. Researchers and medical professionals use these methods to create models that predict patient outcomes, optimize treatment plans, and develop medical technologies.

In essence, the knowledge gained here is foundational for countless career paths and practical scenarios. By strengthening these skills, individuals can enhance their problem-solving abilities and apply mathematical thinking to both professional challenges and daily life. Whether working in technology, business, healthcare, or other fields, the applications of this knowledge are both broad and valuable.

Reviewing Rational Expressions and Equations

Rational expressions and equations form a crucial part of advanced mathematics. These concepts involve the manipulation of ratios of polynomials and solving equations that contain fractions with variables in the numerator and denominator. Understanding how to simplify, multiply, divide, and solve these types of expressions is key to mastering more complex mathematical problems.

When working with rational expressions, one of the first steps is simplifying them. This often involves factoring both the numerator and the denominator and canceling out common factors. Another critical skill is finding the least common denominator (LCD) when adding or subtracting these expressions. This allows for easier manipulation and solving of the equations.

In equations involving rational expressions, it’s important to be cautious about extraneous solutions, which may arise when both sides of an equation are multiplied by a variable-containing denominator. These solutions may not be valid for the original equation, so it’s essential to check each potential solution by substituting it back into the original equation.

Key Steps in Simplifying Rational Expressions

To simplify rational expressions, follow these steps:

• Factor both the numerator and denominator to their simplest form.
• Cancel out any common factors in the numerator and denominator.
• If necessary, find the least common denominator (LCD) for addition or subtraction.
• Perform any additional operations as needed.

Common Mistakes to Avoid

While working with rational expressions and equations, keep in mind these common mistakes to avoid:

Mistake	Solution
Ignoring restrictions on variable values (denominators cannot be zero).	Always check for values that make the denominator zero and exclude them.
Forgetting to simplify before solving equations.	Simplify the expression as much as possible before performing operations.
Failing to check for extraneous solutions.	Substitute potential solutions back into the original equation to verify their validity.

By reviewing these principles and practicing regularly, you can improve your ability to handle rational expressions and equations efficiently, ensuring greater success in solving more complex problems.

Tips for Word Problems in Algebra 2

Word problems can be one of the most challenging aspects of advanced mathematics. They require not only mathematical skills but also the ability to translate real-world scenarios into mathematical equations. To solve these problems efficiently, it’s essential to follow a systematic approach and break down the given information step by step.

Start by carefully reading the problem to understand what is being asked. Identify key pieces of information, such as quantities, relationships, and any conditions that may apply. Highlight or underline these details to ensure they are not overlooked. Once you have a clear understanding of the situation, translate the words into mathematical expressions or equations. This step can often be the most difficult, but with practice, it becomes easier to recognize common patterns and relationships.

One effective technique is to create a diagram or chart to visually represent the problem, especially when dealing with geometric or motion-related scenarios. This helps to organize the data and can make the problem more manageable. Also, don’t be afraid to assign variables to unknown quantities–this can simplify the problem and make it easier to set up and solve equations.

Finally, after solving the problem, always take the time to check your work. Verify that your solution makes sense in the context of the problem, and make sure you’ve answered the question being asked.

Steps for Solving Word Problems

• Read the problem carefully to understand what is given and what is being asked.
• Identify key information such as numbers, units, and relationships between quantities.
• Translate words into mathematical expressions or equations, using variables for unknowns.
• Draw diagrams or charts if applicable to help visualize the situation.
• Set up and solve the equation based on the relationships identified in the problem.
• Check your solution to ensure it makes sense and answers the original question.

By following these tips, you can increase your confidence and accuracy when solving word problems. Remember that practice is key–working through a variety of word problems will help you develop a strong problem-solving strategy and improve your overall understanding of the material.

Focus on Inequalities and Functions

Understanding the relationships between variables is crucial when solving problems involving inequalities and functions. These concepts form the foundation for many advanced mathematical techniques and real-world applications. Mastering them requires an ability to manipulate expressions, interpret their meaning, and solve for unknowns in various contexts.

When dealing with inequalities, it is important to understand how to represent them graphically and algebraically. Inequalities often describe ranges of possible solutions, and being able to interpret these ranges is key. Functions, on the other hand, involve relationships between inputs and outputs. Recognizing different types of functions and knowing how to solve problems involving them is essential for success in higher-level mathematics.

Key Concepts in Inequalities

• Solving linear inequalities: Manipulate the inequality in a similar way as equations, but remember to reverse the inequality sign when multiplying or dividing by a negative number.
• Graphing inequalities: Use a number line or coordinate plane to represent solutions, shading the appropriate regions based on the inequality.
• Compound inequalities: Handle problems involving “and” or “or” conditions by breaking them into simpler inequalities.

Key Concepts in Functions

• Identifying types of functions: Recognize linear, quadratic, exponential, and other types of functions and their properties.
• Function notation: Understand how to interpret function notation and evaluate functions for given inputs.
• Solving function equations: Learn methods for finding the output of a function, or solving for the input when given the output.

Function Type	Graph Characteristics	Example
Linear	Straight line, constant slope	f(x) = 2x + 3
Quadratic	Parabola, symmetric, vertex	f(x) = x^2 – 4x + 3
Exponential	Curve, increases/decreases rapidly	f(x) = 2^x

By focusing on these critical areas and practicing problem-solving strategies, you can build a strong foundation in inequalities and functions. These skills will not only help you succeed in tests but also equip you with the tools needed for more complex mathematical challenges.

How to Stay Calm During the Exam

Staying composed during a test can make a significant difference in your performance. When faced with pressure, it’s easy to feel anxious, but managing your emotions can help you think more clearly and effectively solve problems. Developing strategies to stay calm not only improves focus but also boosts confidence in your ability to tackle challenges head-on.

The key to maintaining calm is preparation and mindset. By following a few simple techniques, you can reduce stress and approach each question with a clear mind. Whether you’re reviewing materials beforehand or managing your time during the session, every effort you make to stay relaxed will contribute to your success.

Pre-Test Strategies

• Prepare in advance: Review the material well ahead of time so you don’t feel rushed on the day of the test.
• Practice relaxation techniques: Deep breathing, visualization, or mindfulness exercises can help calm your nerves.
• Get plenty of rest: A good night’s sleep ensures that your mind is sharp and ready for the challenge.

In-Test Strategies

• Take your time: Read each question carefully and pace yourself. Rushing leads to mistakes and increases anxiety.
• Stay positive: If you get stuck on a problem, move on to the next one and come back later with a fresh perspective.
• Take deep breaths: If you start feeling overwhelmed, pause and take a few slow, deep breaths to reset your focus.
• Remember your preparation: Trust in the work you’ve put in and remind yourself that you are capable of handling the task.

By incorporating these strategies into your routine, you’ll be better equipped to face any challenge that comes your way. The ability to stay calm will help you maintain focus and make smarter decisions, ultimately leading to a more successful performance.

Key Topics to Memorize

Mastering certain foundational concepts is essential for tackling more complex problems. Whether you’re preparing for a challenging assessment or simply aiming to strengthen your understanding, focusing on key topics ensures a solid grasp of the material. Memorizing these core concepts will enable you to solve problems more efficiently and effectively.

Here are some important topics to focus on:

Important Formulas and Rules

• Quadratic Formula: Know how to apply this formula to find the roots of quadratic equations.
• Exponent Laws: Understand the rules for multiplying, dividing, and raising powers of numbers.
• Factoring: Memorize various methods of factoring, such as factoring by grouping and using the difference of squares.
• Properties of Exponents: Familiarize yourself with the laws that govern how to manipulate powers and roots.

Key Functions and Their Graphs

• Linear Functions: Know the slope-intercept form and how to graph lines.
• Exponential Functions: Learn how these functions behave and how to solve related problems.
• Logarithmic Functions: Understand the relationship between logarithms and exponents.
• Rational Functions: Memorize how to manipulate and graph functions involving fractions and polynomials.

Systems and Inequalities

• Solving Systems: Practice solving linear systems using substitution, elimination, and graphing.
• Inequalities: Know how to solve and graph both linear and quadratic inequalities.
• Absolute Value Equations: Memorize how to handle equations involving absolute values.

By committing these concepts to memory, you’ll be equipped with the necessary tools to approach any problem with confidence. These are the building blocks that will support your problem-solving abilities and give you the flexibility to handle diverse challenges.