Algebra 2 Test 3 Answers and Explanations
Successfully navigating through complex mathematical concepts requires more than just memorizing formulas–it involves a deep understanding of how these principles connect and apply in various scenarios. For many students, tackling advanced problem sets can be challenging, especially when facing time constraints and intricate calculations. This section provides the tools and insights you need to approach your assessments with confidence and clarity.
By breaking down common question formats and reviewing critical areas, you can sharpen your skills and improve your ability to solve problems accurately. Whether you’re grappling with equations, functions, or graphing techniques, having a clear strategy can make all the difference. Here, we focus on providing you with a structured approach to mastering essential topics and applying them effectively under exam conditions.
Algebra 2 Test 3 Answer Breakdown
Understanding the structure and solution strategies for challenging problems is crucial for mastering any assessment. This section will guide you through a thorough analysis of common problem types you might encounter, highlighting key steps to reach accurate results efficiently. By breaking down each question into its core components, you’ll learn how to apply critical thinking and essential techniques to tackle even the most complex scenarios.
We’ll explore various methods for simplifying expressions, solving for unknowns, and interpreting data from graphs. Each example is carefully deconstructed to show the logical steps required to arrive at the correct solution. By gaining a deeper understanding of the reasoning behind each answer, you can develop a systematic approach that boosts both your confidence and performance.
Understanding Key Concepts in Algebra 2

Grasping the fundamental principles behind advanced mathematical topics is essential for successfully solving problems and applying techniques effectively. The ability to identify patterns, manipulate equations, and interpret data is the foundation for excelling in more complex exercises. This section focuses on the core ideas that frequently appear in assessments, breaking them down to ensure a clear and thorough understanding.
By focusing on the relationships between variables, functions, and equations, you’ll build the skills necessary to approach a wide range of problems. Mastering these key concepts is not just about memorizing procedures, but about developing the problem-solving mindset that enables you to tackle unfamiliar challenges with confidence and precision.
How to Solve Common Algebra 2 Problems

Solving mathematical problems requires a combination of logical reasoning and familiarity with key techniques. Many exercises follow similar structures, which means understanding the core methods used to solve them can greatly improve both accuracy and speed. In this section, we will explore step-by-step approaches for solving common problem types, highlighting the most effective strategies for getting to the correct solution.
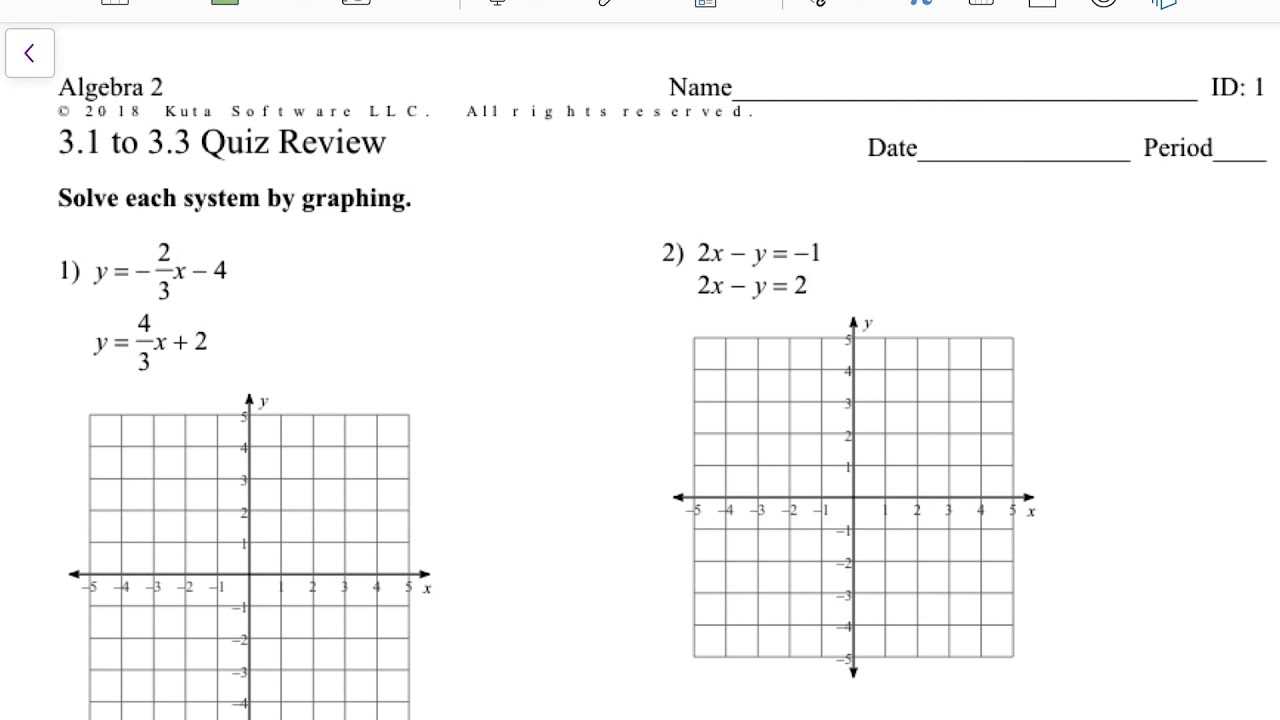
Solving Equations and Inequalities
One of the most common challenges is working with equations and inequalities. These problems often require isolating variables or simplifying expressions to find a solution. The key steps include combining like terms, applying inverse operations, and checking for extraneous solutions when necessary.
| Problem Type | Method | Example |
|---|---|---|
| Linear Equations | Solve for the variable by isolating it on one side | 3x + 5 = 11, x = 2 |
| Inequalities | Use similar steps as equations, but remember to reverse the inequality when multiplying/dividing by a negative number | 2x – 3 > 7, x > 5 |
Graphing Functions
Graphing is another important skill. When tasked with graphing functions, you must understand how to plot key points and interpret the relationships between variables. This involves calculating intercepts, identifying the slope, and understanding how changes in the equation affect the graph’s appearance.
Step-by-Step Solutions for Test 3
Breaking down complex problems into manageable steps is essential for achieving success in assessments. In this section, we will provide a detailed guide for solving typical questions that may appear in the exam, offering clear instructions for each step. By following this approach, you can ensure that you are on the right track and efficiently reach the correct solution.
Solving Linear Equations
When faced with linear equations, the goal is to isolate the variable on one side. Start by eliminating constants and coefficients around the variable, using inverse operations to simplify the equation. It’s important to check your work at each step to avoid common mistakes, especially when dealing with fractions or negative numbers.
| Step | Action | Example |
|---|---|---|
| 1 | Start with the equation | 3x + 4 = 16 |
| 2 | Subtract 4 from both sides | 3x = 12 |
| 3 | Divide both sides by 3 | x = 4 |
Solving Quadratic Equations
Quadratic equations require a different approach. You can solve them using factoring, completing the square, or applying the quadratic formula. Depending on the form of the equation, choose the method that simplifies the process. When solving by factoring, always check if the quadratic expression can be factored easily before moving to more complex methods.
Top Mistakes to Avoid on Algebra 2 Tests
During assessments, it’s easy to overlook key steps or make simple errors that can affect your final result. Recognizing the common pitfalls and taking steps to avoid them will help you improve accuracy and performance. This section highlights the most frequent mistakes students make and provides tips on how to avoid them.
Common Mistakes to Watch Out For
- Skipping important steps when simplifying equations
- Misapplying rules for exponents and radicals
- Forgetting to check for extraneous solutions after solving
- Incorrectly handling negative signs, especially in equations with multiple terms
- Not simplifying the final answer completely
How to Avoid These Mistakes
- Always show your work and check each step carefully before proceeding.
- Review important formulas and operations before starting the problems.
- Ensure that all solutions are valid by plugging them back into the original equation.
- Take your time with negative numbers to avoid sign errors, particularly when distributing.
- Double-check your final answers to ensure they are in the simplest form.
Key Formulas for Algebra 2 Test 3
Mastering key formulas is essential for tackling a wide range of problems in any advanced mathematics exam. These formulas serve as tools to simplify complex calculations and help you solve problems more efficiently. In this section, we will review the most important formulas that are frequently used in assessments, ensuring you’re well-prepared to apply them correctly.
Essential Formulas to Remember
- Quadratic Formula: Used to solve quadratic equations:
x = (-b ± √(b² – 4ac)) / 2a - Slope-Intercept Form: For the equation of a line:
y = mx + b - Point-Slope Form: Another way to express the equation of a line:
y – y₁ = m(x – x₁) - Difference of Squares: Used to factor expressions:
a² – b² = (a + b)(a – b) - Perfect Square Trinomial: For factoring:
a² + 2ab + b² = (a + b)²
Tips for Applying Formulas Effectively

- Understand the context in which each formula is used, as applying the wrong one can lead to mistakes.
- Practice identifying which formulas to use with different problem types to improve speed and accuracy.
- Memorize key formulas early so you can quickly recall them during the assessment.
- When in doubt, break the problem down step-by-step and check that each part of the formula is correctly applied.
Tips for Mastering Algebra 2 Test 3
Achieving success in your assessment requires more than just understanding the material–it’s about developing effective strategies for solving problems efficiently and confidently. In this section, we’ll explore essential tips that will help you sharpen your skills, avoid common pitfalls, and improve your performance during your evaluation.
Effective Study Habits
Establishing a consistent study routine is key to mastering advanced mathematical concepts. Focus on understanding the theory behind each topic, not just memorizing procedures. Practice regularly, and use different methods such as solving practice problems, reviewing notes, and working with peers to reinforce your understanding.
- Set aside dedicated time each day to review concepts and work through problems.
- Use online resources, textbooks, or video tutorials to gain a deeper understanding of complex topics.
- Don’t just passively read–actively solve problems and check your solutions.
Time Management During the Assessment
Managing your time effectively during the evaluation is crucial to ensure you complete all questions thoroughly. Begin by skimming through the entire paper to get an overview, then prioritize questions based on their difficulty. Spend more time on questions that carry higher marks or are more challenging, and make sure to leave time at the end to review your work.
- Allocate a specific amount of time to each section or problem type.
- Start with easier questions to build confidence and gain momentum.
- If stuck on a problem, move on and return to it later if time permits.
How to Manage Your Test Time Effectively
Efficient time management during an examination is essential for maximizing performance. Properly allocating time to different sections of the paper ensures that you have enough time to answer each question thoughtfully while avoiding unnecessary pressure. In this section, we will explore effective strategies for managing your time during assessments.
Planning Your Approach
Before diving into the problems, take a moment to scan the entire exam. This initial review helps you get a sense of the types of questions, their difficulty, and the time needed for each section. Having a clear plan for how to approach the test will help reduce anxiety and keep you focused.
- Quickly review the entire paper before starting.
- Identify the easier questions and tackle them first to build confidence.
- Note which sections or problems are worth more points to prioritize them.
Effective Time Allocation
Once you’ve scanned the exam and formulated a strategy, it’s important to stick to a time limit for each section. Set realistic goals for how long to spend on each problem, ensuring that you don’t get bogged down by one difficult question. Having a clear sense of when to move on can significantly improve your efficiency.
- Divide the total time by the number of sections or questions.
- Spend more time on questions that are more complex or carry higher marks.
- If you’re stuck on a question, move on and come back to it later if time allows.
Reviewing Your Work
Once you’ve completed all the questions, it’s important to leave time to go back and review your answers. This allows you to catch any errors, verify your solutions, and ensure that you haven’t overlooked any questions. A final check can make a significant difference in your overall score.
- Set aside the last 5-10 minutes to review your answers.
- Focus on checking your work for simple mistakes, such as arithmetic errors or missing signs.
- Make sure that every question has been answered to the best of your ability.
Important Topics to Review for Test 3
To perform well on an assessment, it’s crucial to focus on the core concepts that are most likely to appear. By reviewing the key topics in advance, you can ensure that you’re fully prepared to tackle a variety of problems. This section highlights the most important areas to concentrate on for optimal performance.
Key Areas to Focus On
Each problem set may require a deep understanding of specific mathematical principles, and knowing which topics to prioritize can make a significant difference in your ability to answer questions accurately. Here’s a breakdown of the core areas to review:
| Topic | Description |
|---|---|
| Systems of Equations | Understand how to solve systems using substitution and elimination methods, as well as graphing. |
| Factoring Techniques | Be familiar with factoring quadratics, difference of squares, and trinomials. |
| Rational Expressions | Know how to simplify, add, subtract, multiply, and divide rational expressions. |
| Exponents and Radicals | Review the laws of exponents and how to simplify radical expressions. |
| Quadratic Functions | Be prepared to solve problems related to vertex form, standard form, and graphing parabolas. |
Additional Concepts to Review
While the above topics are fundamental, there are other concepts that may appear less frequently but are still essential for comprehensive preparation. These concepts include:
- Logarithmic functions and their properties
- Solving absolute value equations
- Working with exponential growth and decay problems
How to Interpret Algebraic Expressions
Understanding and interpreting mathematical expressions is crucial for solving a wide range of problems. These expressions represent relationships between numbers, variables, and operations, and can often be simplified or manipulated to find a solution. In this section, we will explore strategies for interpreting and breaking down these expressions to help you approach problems with confidence.
The first step in interpreting an expression is identifying the variables, constants, and operations involved. Variables are symbols that stand for unknown values, while constants are known quantities. Operations, such as addition, subtraction, multiplication, and division, define the relationships between these numbers. Once you recognize these components, you can begin to simplify the expression or solve for the unknowns.
For example, in an expression like 3x + 5, x is the variable, 3 is the coefficient (the number multiplying the variable), and 5 is the constant. The operation between the 3 and the variable x is multiplication, and the operation between 3x and 5 is addition. Interpreting this expression involves understanding how these components relate to one another.
By practicing the interpretation of various expressions, you will become more proficient in recognizing patterns and applying the correct methods to solve problems. Whether the expression is simple or complex, breaking it down into its basic parts allows for a clearer and more structured approach to finding a solution.
Common Algebra 2 Test Question Types
Exams often feature a variety of question formats designed to test different mathematical skills and concepts. Understanding the common question types can help you prepare more effectively by focusing on the areas that are most likely to be tested. This section outlines some of the most frequently encountered question types you may face during an assessment.
One common question type involves solving equations. These problems may require you to manipulate algebraic expressions to find the value of a variable. You may be asked to solve linear, quadratic, or rational equations using techniques such as factoring, substitution, or using the quadratic formula.
Another frequent question type involves graphing. These questions require you to plot points or graph functions on a coordinate plane. You may need to graph linear equations, quadratic functions, or other types of mathematical relationships. Some problems might also ask you to interpret the graph, such as identifying the vertex of a parabola or finding the x-intercepts.
There are also word problems that translate real-life scenarios into mathematical equations. These problems test your ability to set up and solve equations based on the information provided. They may involve relationships between quantities, such as rate, time, and distance, or financial scenarios, such as profit and loss calculations.
Additionally, you may encounter problems that test your knowledge of systems of equations. These questions require you to solve for multiple variables simultaneously, often using methods like substitution or elimination.
By familiarizing yourself with these common question types and practicing them in advance, you can approach your assessment with greater confidence and increase your chances of success.
Improving Problem-Solving Speed in Algebra
Mastering the art of solving mathematical problems efficiently is key to performing well under time pressure. Speed doesn’t come from rushing through problems but from a deeper understanding of concepts and practicing effective strategies. In this section, we will explore how to improve your problem-solving speed and accuracy through various techniques and tips.
Practice Mental Math and Shortcuts
One of the best ways to increase your problem-solving speed is to strengthen your mental math skills. Being able to quickly perform basic operations without relying on a calculator can save precious time. For example, learning how to recognize and apply multiplication and division shortcuts can help you tackle larger problems more quickly. Additionally, get comfortable with common formulas and their applications so that you can recall them instantly when needed.
Work on Problem Breakdown and Organization
Another strategy to speed up your problem-solving process is to break problems into smaller, more manageable steps. This approach helps you focus on one part of the problem at a time and prevents you from feeling overwhelmed. Organizing your work in a clear and structured manner, such as writing down intermediate steps, ensures you don’t make careless mistakes and helps you solve the problem more efficiently. Practicing this method regularly will allow you to solve even complex problems with greater speed and confidence.
How to Check Your Algebra 2 Answers
Verifying your solutions is a critical part of problem-solving. After completing a mathematical problem, it’s important to double-check your work to ensure the correctness of your results. This step not only helps you catch mistakes but also reinforces your understanding of the concepts involved. In this section, we will explore effective strategies to verify your solutions and avoid common errors.
Substitute Your Solution Back into the Original Equation
One of the simplest and most reliable methods for checking your work is to substitute your solution back into the original equation. By replacing the variable with your computed value, you can see if both sides of the equation are equal. If they are, your solution is likely correct. This method is especially useful for equations involving variables, as it provides immediate confirmation of your answer.
Check for Consistency and Logical Flow
In addition to substituting values, it’s important to review the logical flow of your solution. Ensure that you followed the correct steps in sequence and didn’t skip any necessary processes. For example, check that you simplified each expression correctly or factored terms when required. Consistency in your approach helps prevent errors and improves the reliability of your results.
Understanding Graphing in Algebra 2
Graphing is an essential tool for visualizing mathematical relationships. By representing equations and inequalities on a coordinate plane, you can gain deeper insights into how different variables interact. In this section, we will explore the fundamental principles of graphing, common techniques, and strategies to ensure accuracy in your graphical representations.
Plotting Points and Understanding Coordinates
To graph any equation, it’s crucial to understand how to plot points correctly on the coordinate plane. Each point is represented by a pair of values (x, y), which correspond to its location relative to the horizontal and vertical axes. Practicing with various equations helps you understand how changing one variable affects the graph’s shape. Start by identifying key points and marking them accurately to form a clearer picture of the relationship between the variables.
Graphing Linear and Non-Linear Equations
Graphing linear equations involves drawing straight lines through points that satisfy the equation, while non-linear equations require more complex curves. For linear equations, identify the slope and y-intercept to plot points and draw a straight line. Non-linear graphs, such as parabolas or hyperbolas, require additional steps, such as identifying key features like the vertex or asymptotes. Understanding the differences between linear and non-linear graphs is key to solving many problems efficiently.
How to Approach Word Problems in Algebra 2
Word problems can often seem overwhelming, but they are an excellent way to apply mathematical concepts to real-world situations. The key to solving these problems is to break them down into smaller, more manageable parts. By identifying the unknowns, setting up the right equations, and translating the words into mathematical expressions, you can solve them efficiently. This section outlines the steps you can follow to approach word problems with confidence.
Step 1: Understand the Problem
Before jumping into solving the problem, take time to read it carefully. Identify the key information provided and determine what is being asked. Highlight or underline important details such as values, relationships, and conditions. Understanding the context of the problem is crucial for setting up the correct equation. It’s also helpful to rephrase the problem in your own words to ensure you fully grasp the scenario.
Step 2: Set Up the Equation
Once you have a clear understanding of the problem, the next step is to translate the given information into a mathematical equation. Identify the variables that represent the unknowns and establish relationships between them based on the problem. Make sure you correctly express the problem’s conditions using appropriate mathematical operations. Below is a simple example:
| Situation | Mathematical Expression |
|---|---|
| A car travels 60 miles per hour for 4 hours. | Distance = Speed × Time (D = 60 × 4) |
| Find the total distance traveled. | D = 240 miles |
By setting up the right equation, you can solve for the unknowns in the problem and verify your solution step by step.
Using Practice Tests for Test 3 Preparation
Practice exams are an invaluable resource when preparing for any examination. They allow you to familiarize yourself with the format of the questions, time constraints, and the types of problems that may arise. Regularly taking these mock exams helps you identify areas of weakness, improve problem-solving speed, and build confidence. This section explores the benefits of using practice tests as a preparation tool and how to effectively integrate them into your study routine.
Step 1: Simulate Real Conditions

One of the main benefits of using practice exams is that they simulate the actual conditions of the examination. Set a timer to replicate the time limits and aim to complete the practice test without interruptions. This will help you manage your time effectively and become accustomed to working under pressure. By practicing under these conditions, you’ll be able to gauge how long you spend on each question and adjust your pace accordingly.
Step 2: Review and Analyze Your Mistakes
After completing a practice exam, take time to carefully review your responses. Identify the questions you struggled with and analyze why you got them wrong. Was it a misunderstanding of the problem? A calculation error? Understanding the source of your mistakes will help you target your review and focus on areas that need improvement. Use this feedback to guide your study sessions, revisiting concepts you found challenging.
Algebra 2 Resources for Further Study
To master the material covered in any advanced mathematical course, it’s essential to go beyond the classroom and make use of various study aids. There are many resources available that can deepen your understanding and help solidify your knowledge. Whether you prefer interactive tools, textbooks, or video tutorials, having access to quality study materials can make a significant difference in your learning process.
Textbooks and Workbooks: A well-structured textbook is invaluable when revisiting foundational concepts and exploring new topics. Workbooks that offer practice problems are especially useful for applying the concepts learned. These materials often provide step-by-step solutions, which can help clarify the approach to solving complex problems.
Online Platforms and Videos: The internet provides an array of interactive platforms and video tutorials. Websites such as Khan Academy, Coursera, and YouTube offer free lessons on a variety of topics, allowing you to watch explanations of difficult concepts at your own pace. Video tutorials often include visual aids, which can be helpful for understanding abstract ideas.
Study Groups and Forums: Connecting with peers in study groups or online forums can be beneficial for collaborative learning. Discussing challenging problems with others allows you to gain different perspectives and insights that you may not have considered on your own. Forums like Stack Exchange or Reddit’s study communities are great places to ask questions and share resources.
By utilizing these resources, you can enhance your preparation and strengthen your understanding of the material.
What to Do After Completing Test 3

Once you’ve finished an assessment, the next step is just as crucial as the preparation itself. It’s important to approach this stage with a clear plan to ensure you reinforce your learning and improve for the future. Reflecting on your performance, identifying areas of weakness, and utilizing effective strategies for review can help solidify your understanding and prevent repeating mistakes.
Steps to Take After Completing the Assessment
- Review Your Work: Carefully go through your completed problems to check for any errors or missed steps. This helps you understand where you might have gone wrong and identify areas to focus on for improvement.
- Analyze Common Mistakes: Pay attention to patterns in your mistakes. Were there specific types of problems you struggled with more than others? Identifying these will help you direct your study efforts more efficiently.
- Ask for Feedback: If possible, discuss your performance with your instructor or a peer. Getting feedback can provide insight into areas that need further attention and clarify any misunderstandings.
Strategies for Effective Follow-Up
- Practice More Problems: Focus on additional problems in the areas you found most challenging. The more you practice, the more comfortable you’ll become with different types of problems.
- Use Resources for Review: Revisit any study guides, videos, or textbooks that cover the material. These resources can reinforce concepts and offer alternative explanations for tough topics.
- Track Your Progress: Keep track of your improvements by re-assessing similar problems in the future. This will help you see your growth and identify any remaining weak spots.
By taking these steps, you ensure that the completion of the assessment is just one part of an ongoing learning process that strengthens your understanding and prepares you for future challenges.