AP Stats 2006 Free Response Answers

When preparing for complex assessments in mathematics, it is essential to develop a solid understanding of the underlying principles and techniques. Tackling advanced questions requires more than just memorizing formulas; it demands the ability to analyze data, think critically, and present logical solutions clearly and concisely.

Practical examples can significantly enhance one’s problem-solving abilities. By carefully studying real test scenarios, students can gain valuable insights into how to approach difficult tasks, recognize patterns, and apply the right methods under time constraints.

In this section, we will explore some key problems from a past examination, breaking them down to show step-by-step solutions and highlighting the thought process behind each. Whether you’re revisiting old material or preparing for future challenges, this guide will provide the tools you need to succeed and improve your skills.

AP Exam Overview

The exam in question is designed to assess a deep understanding of mathematical concepts and the ability to apply them in real-world scenarios. It tests both theoretical knowledge and practical problem-solving skills. Candidates are expected to demonstrate their proficiency in analyzing data, interpreting results, and providing well-reasoned explanations for their solutions.

The assessment is typically divided into multiple sections, each focusing on different aspects of the subject. These sections require students to tackle a variety of problems, ranging from basic calculations to more complex analytical tasks. Preparation involves mastering both fundamental techniques and advanced methodologies, ensuring that students can handle all question types effectively.

Section	Focus Area	Time Allotted
Part 1	Multiple Choice	1 hour
Part 2	Problem Solving	1 hour 30 minutes
Part 3	Written Explanation	1 hour

Success on the exam requires not only mastering content but also practicing time management, ensuring each section is completed efficiently. By reviewing past tests and understanding the typical structure and difficulty of the questions, students can greatly enhance their chances of performing well.

How to Approach Problem Solving Tasks

When tackling complex tasks in an exam, it is crucial to remain focused and methodical. Each question is an opportunity to showcase your understanding and apply problem-solving techniques. Successful completion of such questions requires not just the correct answer but also a clear and logical presentation of your thought process.

Step-by-Step Approach

Begin by carefully reading the problem and identifying the key components. Often, the question will contain valuable information that will guide you towards the appropriate solution method. Once you understand what is being asked, break the problem down into smaller, manageable steps. Here’s how you can proceed:

• Read the question thoroughly and highlight important data.
• Identify which mathematical methods are applicable to the problem.
• Formulate a plan for solving the task.
• Execute the solution step by step, showing all work clearly.
• Double-check your solution and verify that it answers the question completely.

Common Pitfalls to Avoid

Many candidates make the mistake of rushing through these tasks without a clear strategy, leading to errors. To avoid this, focus on the following:

1. Don’t skip over details. Small pieces of information can often lead to a correct solution.
2. Don’t assume that your first approach is always the best. Reevaluate if the solution doesn’t make sense.
3. Avoid leaving work or steps incomplete. A well-documented process is crucial, even if the final answer is incorrect.

By staying organized, following a systematic process, and paying attention to all aspects of the problem, you can greatly improve your performance on such tasks and increase your chances of success.

Understanding Key Concepts from 2006

Mastering the foundational principles behind challenging problems is essential for tackling any complex exam. By fully grasping core ideas and methods, students can approach questions with greater confidence and clarity. The concepts from the past examination serve as an excellent framework for refining problem-solving skills and ensuring a deeper understanding of the subject matter.

Critical Topics to Review

The following concepts were central to many of the tasks, and understanding them thoroughly can lead to improved performance:

• Probability distributions and their properties.
• Understanding correlation and regression analysis.
• Interpreting data sets and identifying trends.
• Analyzing variability and measures of central tendency.
• Applying statistical inference methods correctly.

Approaching Problem Scenarios

For many candidates, the most challenging part is not just applying formulas but understanding the real-world context behind each problem. Here are key strategies to effectively engage with each task:

1. Start by identifying what type of problem you’re dealing with–whether it’s related to analysis, probability, or inference.
2. Extract all relevant data and organize it clearly before starting your calculations.
3. Always justify your reasoning, especially when applying a formula or method to ensure logical consistency.
4. When analyzing results, consider their practical implications to provide meaningful interpretations.

Focusing on these concepts and strategies will enable you to tackle similar tasks with greater precision and insight, enhancing your ability to perform well on future assessments.

Common Mistakes to Avoid in Responses

When solving complex problems, it’s easy to make small but significant mistakes that can impact your results. These errors often occur when students rush through questions or overlook key details. Understanding the common pitfalls can help you avoid these mistakes and improve the quality of your solutions.

Common Errors to Watch Out For

Here are some of the most frequent mistakes students make when tackling such problems:

• Failing to read the question carefully, leading to misinterpretation of the task.
• Omitting essential steps or explanations that demonstrate how the solution was reached.
• Relying too heavily on formulas without fully understanding when or how to apply them.
• Neglecting to double-check calculations, which can lead to minor errors that affect the final result.
• Providing vague or incomplete explanations instead of clear, step-by-step reasoning.

How to Avoid These Mistakes

By being mindful of these common issues, you can improve your responses and ensure a more accurate and thorough solution:

1. Take your time to read and understand each question before beginning.
2. Work through each step carefully, ensuring you explain your reasoning along the way.
3. Practice applying concepts in different contexts to develop a deeper understanding of when each method is appropriate.
4. Double-check your work and verify that each calculation and interpretation makes sense in the context of the problem.

By avoiding these mistakes and focusing on precision and clarity, you’ll be better equipped to perform well and deliver accurate solutions. Practicing these habits will also help you become more confident in your problem-solving skills over time.

Essential Tips for AP Success

Achieving success on an advanced mathematics exam requires more than just understanding formulas. It involves strategic preparation, effective time management, and the ability to apply learned concepts in diverse scenarios. With the right approach, you can improve your performance and approach each problem with confidence and clarity.

Preparation Strategies

To excel, it’s important to prepare both mentally and practically. Focus on the following key strategies to optimize your study sessions:

• Practice regularly with past exams and sample problems to build familiarity with the types of tasks you’ll encounter.
• Understand the theoretical foundations behind each concept so you can apply them flexibly in different situations.
• Review the scoring guidelines to understand how your work will be evaluated and what details are most important.
• Break down complex problems into smaller, more manageable steps to reduce the likelihood of error.

Exam Day Tips

On the day of the exam, maintaining focus and managing time effectively is key. Consider the following tips:

• Read each question carefully to ensure you understand what is being asked before you start solving.
• Manage your time wisely by allocating enough time to tackle every problem, but don’t get stuck on one question.
• Start with the questions you find easiest to build confidence, then move on to more challenging ones.
• Review your solutions thoroughly to catch any mistakes before submitting your work.

By following these strategies and staying focused, you can enhance your chances of performing well and achieving success on your exam.

Breaking Down the Exam Problems

Analyzing complex problems and understanding the methods used to solve them is essential for mastering any exam. By breaking down each task into smaller, more manageable steps, students can better identify key concepts and apply the correct techniques to arrive at the right solutions. This approach not only helps in solving individual questions but also reinforces the overall understanding of the subject.

In this section, we will dissect some of the most challenging problems from a past exam, demonstrating the logical steps required to solve them. By focusing on the thought process behind each solution, you can learn to identify patterns, make connections, and approach future problems with greater ease and accuracy.

Each problem often contains specific elements that are critical to solving it correctly. Understanding how to navigate through the data and interpret the information effectively is crucial. With careful attention to detail and the application of solid problem-solving strategies, any question can be broken down and solved systematically.

Detailed Analysis of Problem 1

Breaking down the first problem of the exam is crucial for understanding how to approach similar questions. By closely examining the question and carefully going through each step of the solution, you can gain insights into the process and strategies required for success. This detailed analysis will help clarify the thought patterns behind the solution and highlight key techniques that are essential in tackling similar problems.

Understanding the Problem

The first step is to understand the problem’s context and the information provided. Often, such questions include data that needs to be interpreted and analyzed. Pay close attention to the question’s wording and identify what is being asked. In many cases, the problem will require breaking down a complex scenario into simpler components for easier analysis.

Step-by-Step Solution

Once you have a clear understanding of the problem, the next step is to outline the method for solving it. Begin by identifying any relevant formulas, concepts, or procedures that should be applied. Be sure to show all work clearly and explain each step logically. This helps ensure that each part of the problem is addressed systematically.

• Step 1: Extract and organize the given data.
• Step 2: Choose the appropriate techniques to analyze the data.
• Step 3: Apply the methods and calculate the solution.
• Step 4: Interpret the results and ensure they align with the question’s requirements.

By following this structured approach, you’ll be able to solve the problem with confidence and provide a well-supported answer. Taking your time to analyze each step carefully will improve your problem-solving skills and set a strong foundation for tackling other similar challenges.

How to Interpret Statistical Data

Interpreting data is a critical skill in many fields, as it allows you to draw meaningful conclusions from raw numbers and patterns. The ability to analyze and make sense of data is essential for solving problems and making informed decisions. Whether you are working with averages, percentages, or distributions, understanding how to interpret the results accurately can significantly impact the outcome of your analysis.

To begin interpreting statistical information, it’s important to identify the type of data you are dealing with and the context in which it was collected. Once you have this understanding, you can choose the appropriate methods for analysis, such as calculating central tendencies, measuring variability, or assessing relationships between variables. Each technique provides a different perspective on the data, and combining multiple approaches often leads to the most comprehensive insights.

While interpreting data, always ask yourself what the numbers represent and how they relate to the broader question or hypothesis. This perspective will guide you through the process of drawing logical conclusions and ensuring that your interpretations are both accurate and meaningful.

Important Formulas for Success

Understanding key formulas is fundamental to solving problems effectively. In any exam focused on data analysis and interpretation, having a solid grasp of essential mathematical concepts is crucial. These formulas are the building blocks that help you work through complex questions efficiently, providing the foundation for sound decision-making and accurate conclusions.

Key Formulas to Remember

Here are some of the most commonly used formulas that you should keep in mind:

• Mean: The average value, calculated by summing all data points and dividing by the number of points. (Mean = Σx / n)
• Variance: A measure of the spread of data points, calculated by averaging the squared differences from the mean. (Variance = Σ(x – Mean)² / n)
• Standard Deviation: The square root of variance, providing a measure of how much individual data points deviate from the mean. (Standard Deviation = √Variance)
• Probability: The likelihood of an event occurring, calculated as the number of favorable outcomes divided by the total possible outcomes. (P(E) = Number of favorable outcomes / Total number of outcomes)
• Confidence Interval: A range of values used to estimate the true population parameter with a certain level of confidence. (CI = Mean ± (Z * (Standard Deviation / √n)))

Using Formulas Effectively

While memorizing formulas is important, knowing when and how to apply them is equally critical. Understanding the context of each question and selecting the appropriate formula to use ensures that your answers are both accurate and relevant. Take time to practice these formulas with different types of data and scenarios to develop a deeper understanding of their application.

Strategies for Time Management on the Exam

Effective time management during an exam is crucial for completing all tasks thoroughly and accurately. It’s easy to get caught up in difficult questions, but balancing your time ensures that you can address all sections of the test. With the right strategies, you can avoid feeling rushed and give each question the attention it deserves.

One of the most effective techniques is to allocate a specific amount of time to each question based on its difficulty and point value. This helps you stay on track without spending too much time on any one part of the exam. Additionally, consider starting with the questions that you feel most confident about, as this will boost your momentum and allow more time for tougher problems later on.

• Plan Your Approach: Quickly skim through the entire exam before starting to identify questions that seem easier or more straightforward.
• Set Time Limits: Assign a reasonable time limit for each question, and stick to it as closely as possible to avoid getting bogged down by one question.
• Keep Track of Time: Regularly check the clock to ensure you’re on pace to finish all sections, and adjust if necessary.
• Don’t Overthink: If you’re stuck on a question, move on and come back to it later. Avoid wasting valuable time overanalyzing difficult parts.
• Review Your Work: If time permits, set aside a few minutes at the end to quickly review your answers and make any necessary corrections.

By practicing these strategies in advance, you’ll be better prepared to manage your time efficiently during the exam, ensuring that you can showcase your full potential and complete the test with confidence.

Examining Problem 2: Solutions and Insights

Problem 2 presents an opportunity to apply analytical skills to real-world scenarios. In this section, we will break down the problem into manageable steps, offering detailed solutions and key insights. By understanding the approach to solving this problem, you will gain a deeper understanding of the concepts involved and how to tackle similar questions in the future.

Breaking Down the Problem

The first step is to carefully analyze the question and identify the critical elements. Pay attention to the data provided, the assumptions that can be made, and the calculations needed. In many cases, approaching the problem systematically will lead to a solution faster and with fewer mistakes.

• Step 1: Read through the problem statement to identify all relevant information.
• Step 2: Determine what is being asked and what data you have to work with.
• Step 3: Apply the appropriate formula or method based on the type of problem you are solving.

Key Insights and Common Pitfalls

Understanding the underlying concepts and recognizing common mistakes is essential to ensuring that you arrive at the correct solution. Here are some key insights that can help you avoid errors and refine your approach:

• Insight 1: Make sure to check your calculations at every step to avoid small errors that can add up.
• Insight 2: Always recheck the units and ensure consistency when applying formulas or methods.
• Common Pitfall: Avoid rushing through the problem; it’s important to stay focused and methodical.

By following this structured approach, you can not only solve Problem 2 effectively but also build a strong foundation for solving similar challenges in the future. The insights provided here will guide you in understanding the logic behind the solutions and give you the confidence to tackle a variety of exam questions with ease.

How to Write Clear and Concise Answers

Effective communication is key when responding to exam questions. Writing clear and concise responses ensures that your understanding is communicated accurately and efficiently. Avoiding unnecessary details and focusing on the essentials allows you to express your thoughts in a way that is easy to follow and comprehend.

To achieve clarity, it’s important to structure your answers logically, using appropriate terminology and providing explanations where needed. The goal is to convey your reasoning in a manner that is both straightforward and precise, without overcomplicating your response. This approach not only helps you answer questions accurately but also saves valuable time during the exam.

• Be Direct: Start your response with the main point or answer before elaborating on supporting details.
• Use Simple Language: Avoid overly technical jargon unless it is necessary, and explain any terms that might be unclear to the reader.
• Stay Focused: Address only the relevant parts of the question. Resist the urge to add extra information that doesn’t directly contribute to your answer.
• Organize Your Thoughts: Break your response into clear steps or logical segments to guide the reader through your reasoning.
• Review and Edit: After writing your response, take a moment to check for clarity and ensure you’ve removed any unnecessary information.

By applying these principles, you can write answers that are both easy to understand and thorough, demonstrating your knowledge effectively while ensuring that you meet the requirements of the exam.

Understanding Grading Criteria for Free Responses

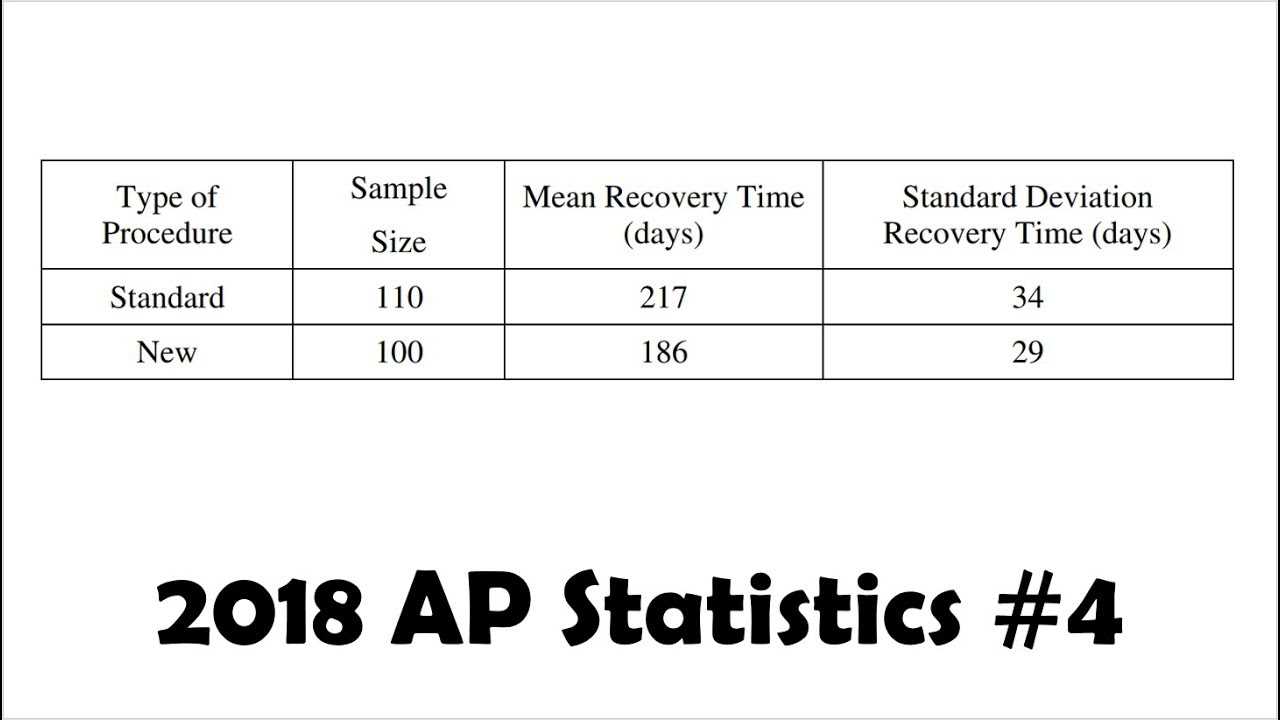
When preparing for exams that require written responses, it’s essential to understand the grading criteria. Knowing how your answers will be evaluated helps you focus on the key elements that contribute to earning full marks. Graders look for specific aspects in each response, such as clarity, accuracy, and the logical flow of your reasoning. By aligning your responses with these expectations, you can maximize your performance.

Each question typically has a set of criteria that breaks down the points available. These criteria usually include the following components: identifying the right approach, applying correct methods, justifying your steps, and presenting a well-organized explanation. Graders will assess how well you meet these expectations, so it’s important to ensure your answer is not only correct but also clearly communicated.

• Correct Method: The solution should reflect the appropriate methods and techniques for solving the problem.
• Logical Flow: Your reasoning must be clear and coherent, demonstrating how you arrived at your conclusion step by step.
• Justification: Every step of the process should be supported by an explanation or a clear rationale.
• Clarity: Avoid unnecessary jargon or overly complex explanations. Ensure that each part of your response is easy to understand.
• Conciseness: While it’s important to be thorough, responses should also be concise. Focus on the essential information needed to answer the question.

By understanding the grading criteria and focusing on these key areas, you can improve the quality of your written responses and increase your chances of achieving a higher score. Ensure that each part of your answer meets the outlined expectations, and you will demonstrate your mastery of the subject matter effectively.

Preparing for Advanced Statistical Questions

When preparing for complex questions that require in-depth analysis, it’s crucial to develop a solid understanding of advanced concepts and methodologies. These types of questions often demand more than just basic knowledge; they require the ability to apply multiple concepts simultaneously and present well-reasoned explanations. Proper preparation not only involves knowing the material but also practicing how to approach intricate problems efficiently and accurately.

To tackle these challenges effectively, focus on building a strong foundation in core principles, such as data analysis, probability theory, and hypothesis testing. With practice, you’ll gain confidence in identifying the best approach for solving problems and interpreting results accurately. The key to success is not just solving the problem, but explaining your reasoning clearly and methodically.

Concept	Key Focus	Preparation Tips
Probability	Understanding different types of probability distributions	Practice solving problems with various distributions like normal, binomial, and Poisson
Data Analysis	Ability to summarize and interpret large data sets	Work with real-life data to calculate means, medians, standard deviations, and identify trends
Hypothesis Testing	Formulating null and alternative hypotheses and performing tests	Master different tests like t-tests, chi-square tests, and ANOVA
Regression	Interpreting relationships between variables	Practice fitting linear regression models and understanding residual plots

By mastering these key areas and honing your problem-solving skills, you’ll be well-equipped to approach more advanced questions confidently. Whether it’s understanding the mathematical foundations or applying methods to real-world data, each step will bring you closer to achieving success in tackling complex problems on your exam.

Reviewing Key Topics from AP Stats 2006

In preparation for tackling comprehensive questions, it’s essential to revisit and solidify understanding of core concepts. These subjects are foundational to mastering the subject and addressing complex challenges effectively. By reviewing the main topics from the previous exam, you can sharpen your skills and better apply the theoretical knowledge to real-world scenarios. Each topic provides critical tools to analyze and interpret data, an essential part of excelling in this subject.

Focusing on areas such as data analysis, probability distributions, and hypothesis testing is particularly important. These are fundamental aspects of the exam and will recur in various forms. Additionally, understanding relationships between variables, interpretation of graphs, and advanced mathematical calculations are key skills to develop. By mastering these concepts, you’ll be prepared to approach any question with confidence and clarity.

Here are some of the most important topics to focus on:

• Data Collection and Organization: Learn how to gather, organize, and summarize data accurately to identify trends and patterns.
• Probability Theory: Understand different types of distributions, including normal, binomial, and Poisson, and their applications.
• Inference and Hypothesis Testing: Develop the skills to perform and interpret various tests, including t-tests, chi-square tests, and confidence intervals.
• Regression Analysis: Focus on linear regression, understanding residuals, and interpreting coefficients and their significance.
• Graphical Representations: Practice creating and interpreting histograms, scatterplots, boxplots, and other visual tools to represent data.

By revisiting these key concepts, you’ll be better equipped to address both theoretical and applied questions. This review process is crucial for reinforcing your knowledge and ensuring you’re ready for the challenges ahead.

What to Do After Completing the Exam

Once the exam is finished, it’s essential to take a step back and reflect on your performance. While it’s natural to feel a sense of relief, it’s also a good time to evaluate the process and plan your next steps. This period after completing the exam can significantly influence your mindset moving forward, helping you prepare for the results or future academic challenges.

Immediately after the exam, take a moment to relax and decompress. Exam periods can be stressful, and giving yourself some time to unwind will help you clear your mind. Engage in activities that help reduce stress, such as taking a walk, listening to music, or chatting with friends.

Once you’ve had time to relax, it’s helpful to review your performance mentally. You can analyze the questions you felt confident about and those that seemed more challenging. This self-reflection can help you pinpoint areas that may need further review or preparation for future exams. However, avoid overthinking individual questions or stressing about parts you were unsure about. Trust the preparation you’ve done up until this point.

Another productive step is to seek feedback from teachers or peers. If you have access to any exam materials, discussing them with classmates or instructors can offer new insights and help you understand your strengths and weaknesses. This feedback can also guide you in focusing your studies in the future.

Finally, take time to rest before diving into your next challenge. Whether it’s preparing for another subject or focusing on personal growth, ensuring you’re recharged will allow you to approach upcoming tasks with a fresh perspective. Remember, the process of preparing for and completing an exam is just one part of your academic journey, and each experience helps you grow.