Solution to the 100 Locker Problem

Imagine a scenario where a series of containers are initially in a closed state. Each of these containers undergoes a series of actions based on certain conditions, creating an intriguing challenge to determine which ones remain open at the end. The puzzle is simple to explain but complex to solve, requiring both logical reasoning and mathematical understanding.

As you delve into the steps, you’ll find that the pattern of actions taken to open or close these containers follows a predictable rhythm. The core of the challenge lies in recognizing how the containers’ states change over time and how specific numbers play a crucial role in the outcome. By analyzing these transitions and using a methodical approach, it becomes clear which containers will be left open.

The beauty of this puzzle is in its simplicity and the unexpected insights it offers about divisibility, number theory, and patterns. It not only provides a fun mental exercise but also highlights deeper mathematical concepts that extend far beyond the confines of the puzzle itself. Understanding the underlying principles can open doors to a variety of similar logical challenges.

Understanding the 100 Locker Problem

This puzzle presents a scenario where a set of closed containers undergoes a series of actions, leading to a shift between open and closed states. The task is to determine which containers remain open after a sequence of operations, with each action involving toggling the state of certain containers. The puzzle’s simplicity is deceptive, as it requires a deeper understanding of how numbers and their divisors influence the outcome.

The key to solving this challenge lies in recognizing a fundamental pattern. Each container is toggled multiple times depending on its number. The sequence of switches follows a specific order, and the challenge is to predict which containers will be left in the open position after all actions are completed. Through careful analysis, the solution reveals a fascinating connection between the number of divisors a container’s position has and its final state.

What makes this puzzle particularly intriguing is its connection to number theory. As you examine the process, you’ll see how divisibility plays a central role in determining which positions are toggled an odd or even number of times. By leveraging these mathematical insights, the seemingly complex situation becomes much clearer, leading to a satisfying resolution.

Mathematical Concepts Behind the Puzzle

At the heart of this challenge lies a mathematical principle rooted in divisibility. The key to understanding the solution is recognizing how numbers influence the toggling of each container. The process is determined by the number of times each position is toggled, which depends on the divisors of the position number. In other words, each container is toggled for every number that divides its position, creating a pattern that directly affects the final state of the container.

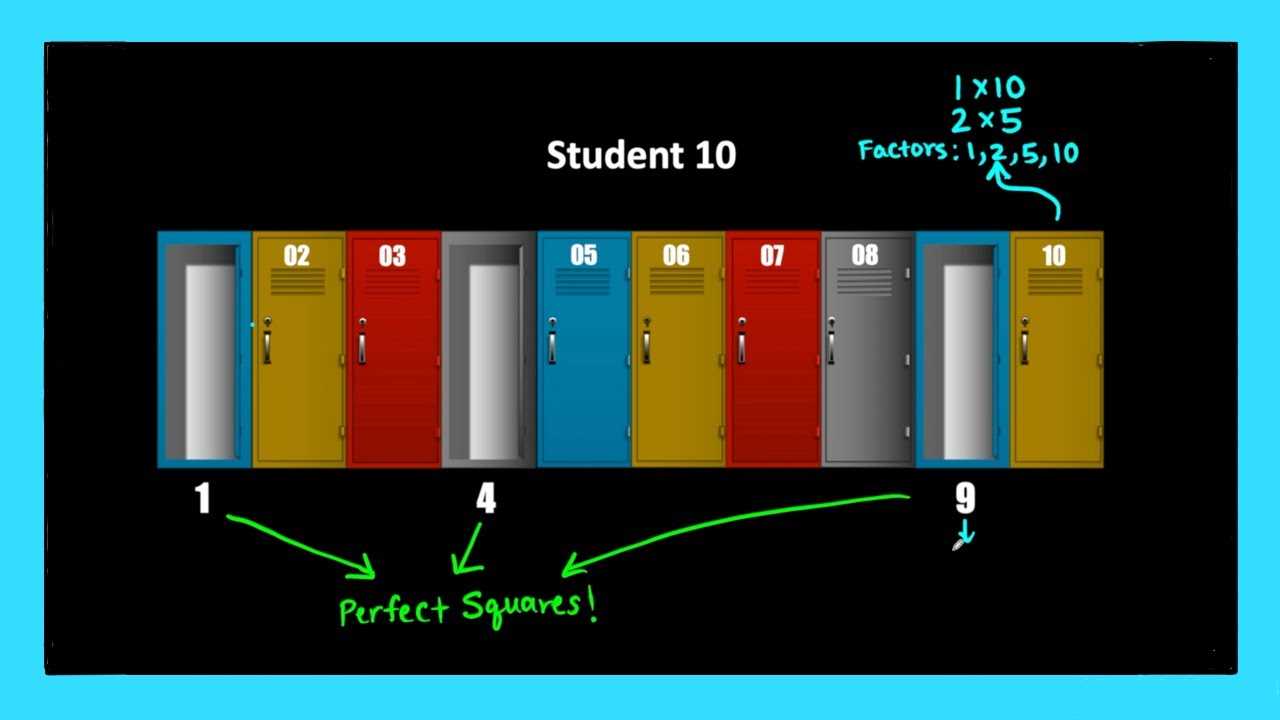
The crucial observation is that positions with an odd number of divisors will end up open, while those with an even number of divisors will be closed. This is because each toggle flips the container’s state, and an odd number of toggles leaves the container open, while an even number of toggles returns it to the closed state. The interesting aspect of this pattern is that only perfect squares have an odd number of divisors, as they are the only numbers where a divisor pairs with itself.

Position	Divisors	Number of Divisors	Final State
1	1	1	Open
2	1, 2	2	Closed
3	1, 3	2	Closed
4	1, 2, 4	3	Open
9	1, 3, 9	3	Open
16	1, 2, 4, 8, 16	5	Open

This pattern extends across the entire sequence, with only those positions that are perfect squares remaining open at the end of the process. This insight is the key to solving the puzzle, revealing the underlying mathematical structure that governs the entire system.

Initial Conditions and Assumptions

To begin solving this puzzle, it’s essential to define the starting conditions that govern the process. The scenario assumes a series of containers that are initially all in a closed state. Each container will undergo a series of actions that change its state, either opening or closing it, based on specific rules. These actions follow a systematic pattern, with each action targeting certain positions in the sequence.

Rules of Toggling

The fundamental rule is that each container is toggled multiple times, depending on the position it occupies. A container will be toggled whenever a divisor of its position is encountered. For instance, the container in position 6 will be toggled during the first, second, third, and sixth steps, since these are the divisors of 6. The toggling sequence is what determines whether a container ends up open or closed at the end of the process.

Assumptions for the Puzzle

One key assumption is that every position starts in a closed state, and only the toggling process changes this state. Additionally, it is assumed that each toggle operation is independent and does not affect other containers directly. The puzzle also assumes that all containers will undergo the same number of toggling operations, making the solution consistent for all positions. These assumptions are the foundation upon which the solution is built, as they allow us to focus on the mathematical relationships between the positions and their divisors.

Key Insights into Locker Switching

Understanding the process of toggling containers is essential to solving this puzzle. The core idea behind the switching process is that each container is toggled multiple times, with each toggle changing its state from closed to open or vice versa. The number of times a container is toggled depends on the number of divisors its position has. This simple yet powerful insight helps uncover the pattern that ultimately determines which containers remain open at the end.

How Divisibility Affects the Outcome

The most important observation is how divisibility impacts the toggling process. A container is toggled once for every divisor of its position number. For example:

• Position 6 has divisors 1, 2, 3, and 6, so it will be toggled 4 times.
• Position 9 has divisors 1, 3, and 9, so it will be toggled 3 times.
• Position 16 has divisors 1, 2, 4, 8, and 16, so it will be toggled 5 times.

What makes this interesting is that toggling an even number of times returns the container to its original state (closed), while an odd number of toggles leaves it open. Thus, the key to solving this puzzle is recognizing that only positions with an odd number of divisors will remain open, and these positions correspond to perfect squares.

The Role of Perfect Squares

Perfect squares are the only positions that have an odd number of divisors. This happens because, in the case of a perfect square, one of the divisors is repeated (for example, the number 36 has divisors 1, 2, 3, 4, 6, 9, 12, 18, and 36, where 6 is repeated). As a result, positions such as 1, 4, 9, 16, 25, and so on, will be toggled an odd number of times and remain open. All other positions, which have an even number of divisors, will be closed at the end.

1. Perfect square positions remain open.
2. Non-perfect square positions are closed.

This insight is the foundation of the solution to the puzzle, allowing you to predict which containers will stay open without having to manually toggle each one.

Exploring Patterns in Locker Behavior

When analyzing the behavior of the containers throughout the toggling process, certain patterns emerge that reveal key insights into their final states. At first glance, the sequence of changes may seem random, but a closer inspection uncovers a predictable structure. The pattern is determined by the divisors of each container’s position, with the number of divisors directly influencing how often it is toggled and whether it ends up open or closed.

One of the most striking patterns is that containers with perfect square positions always remain open. This is because they are toggled an odd number of times, as their divisors include a repeated value. On the other hand, containers in non-perfect square positions are toggled an even number of times and return to their initial closed state.

Let’s break down how the toggling works and look at some examples of this pattern in action:

• Container 1 is toggled once (divisors: 1) and remains open.
• Container 4 is toggled three times (divisors: 1, 2, 4) and remains open.
• Container 9 is toggled three times (divisors: 1, 3, 9) and remains open.
• Container 16 is toggled five times (divisors: 1, 2, 4, 8, 16) and remains open.
• Container 2 is toggled twice (divisors: 1, 2) and stays closed.

This pattern becomes more evident as the number of containers increases. By understanding the relationship between the number of divisors and the toggling sequence, we can predict with certainty which containers will remain open by simply identifying the perfect square positions.

Analyzing the First Few Steps

The first few actions in this puzzle set the stage for the subsequent toggling process. Understanding how the containers are affected during these initial steps is crucial for recognizing the underlying pattern that governs their final states. These early moves provide insight into how each container’s position will influence its toggling throughout the process.

During the first step, every container is toggled because all positions are divisible by 1. This means that after the first action, every container will be open. As the sequence progresses, the toggling becomes more selective, with only certain containers being affected at each step based on the divisibility of their positions. For example, in the second step, only even-numbered containers will be toggled, as 2 is the only divisor for those positions. This selective toggling continues throughout the process, creating a series of open and closed states that follow a predictable pattern.

To see how this works in practice, consider the following sequence of actions:

• After step 1, all containers are open (divisible by 1).
• After step 2, only containers in even-numbered positions are toggled (divisible by 2).
• After step 3, only containers in positions divisible by 3 are toggled (divisible by 3).
• After step 4, only containers in positions divisible by 4 are toggled (divisible by 4).

As the steps progress, the toggling pattern becomes more refined, and it becomes clear that the state of each container is determined by the number of divisors it has. This early phase of the puzzle illustrates the foundational concept that the number of divisors dictates whether a container will end up open or closed.

The Role of Prime Numbers in the Puzzle

Prime numbers play a significant role in the toggling process of the containers. Their unique property of having only two divisors–1 and themselves–sets them apart from other numbers and influences the final state of containers positioned at prime-numbered spots. Understanding how prime numbers behave in this context helps clarify why certain positions remain open at the end of the process.

How Primes Influence Toggling

When considering a prime number, it is important to note that it will only be toggled twice: once for 1 and once for the number itself. This means that prime-numbered positions will always be toggled an even number of times, and since they start in a closed state, they will end up closed as well. This characteristic is true for all prime-numbered positions, regardless of how large the number is.

• Position 2: Toggled twice (divisors: 1, 2) and closed at the end.
• Position 3: Toggled twice (divisors: 1, 3) and closed at the end.
• Position 5: Toggled twice (divisors: 1, 5) and closed at the end.
• Position 7: Toggled twice (divisors: 1, 7) and closed at the end.

Impact on Non-Prime Positions

On the other hand, non-prime positions have more than two divisors, meaning they are toggled more times. The number of divisors a position has directly determines whether it will remain open or closed. For example, composite numbers, which have more divisors, are toggled an odd number of times if the divisors include a repeated value, leaving them open at the end. In contrast, prime positions, with only two divisors, always get toggled an even number of times, resulting in a closed state.

Understanding the distinction between prime and non-prime numbers helps explain why only those positions corresponding to perfect squares remain open. Perfect squares are the exception, as they have an odd number of divisors, which leads to an open state. Thus, prime numbers help reinforce the rule that containers with an even number of divisors will be closed by the end of the toggling sequence.

How the Number of Divisors Affects the Solution

The number of divisors a position has is a crucial factor in determining whether a container will remain open or closed at the end of the sequence. Each toggle action depends on the divisors of the container’s position, and the number of times a container is toggled directly influences its final state. Understanding this relationship is essential for predicting which containers will remain open after all steps have been completed.

When a position has an even number of divisors, the container will be toggled an even number of times, resulting in it being closed at the end. Conversely, positions with an odd number of divisors are toggled an odd number of times, and these containers will remain open. This distinction arises because divisors typically come in pairs, except when a number is a perfect square, where one divisor is repeated (for example, the number 36 has divisors 1, 2, 3, 4, 6, 9, 12, 18, and 36, with 6 being repeated). As a result, perfect square positions are the only ones with an odd number of divisors and therefore remain open.

Let’s explore how this plays out with a few examples:

• Position 6 has divisors 1, 2, 3, and 6, so it is toggled four times (even number) and ends up closed.
• Position 9 has divisors 1, 3, and 9, so it is toggled three times (odd number) and remains open.
• Position 16 has divisors 1, 2, 4, 8, and 16, so it is toggled five times (odd number) and stays open.
• Position 10 has divisors 1, 2, 5, and 10, so it is toggled four times (even number) and ends up closed.

By examining the number of divisors, we can clearly see that positions with an even number of divisors are closed, while those with an odd number are open. This principle is key to solving the puzzle, and it underscores the importance of divisibility in determining the final state of each container.

Why Some Lockers Stay Open

In this puzzle, certain positions remain open after all the toggling steps have been completed. The key to understanding why some containers remain open lies in the number of divisors each position has. Each toggle action is determined by whether the position number is divisible by the step number, and this process ultimately affects whether the container ends up open or closed.

Containers are toggled each time their position number is divisible by a given step number. Normally, divisors come in pairs: for example, 12 has divisors 1, 2, 3, 4, 6, and 12. This means the container at position 12 will be toggled six times. However, for some numbers, one of their divisors is repeated. This happens with perfect squares–numbers like 1, 4, 9, 16, and so on. These numbers have an odd number of divisors because one of their divisors is repeated (e.g., 16 has divisors 1, 2, 4, 8, and 16, with 4 appearing twice).

Because positions with an odd number of divisors are toggled an odd number of times, these containers will end up in the opposite state from their initial one. Since they start in a closed state, they will be left open. Conversely, positions with an even number of divisors are toggled an even number of times, so they remain closed.

To summarize, containers that correspond to perfect squares–such as position 1, 4, 9, 16, and so on–remain open because they have an odd number of divisors. These positions are the only ones that remain open at the end of the process, making them a key part of solving the puzzle.

Understanding the Mathematical Proof

The solution to this puzzle relies on understanding the mathematical reasoning behind the toggling process. The key to the proof is recognizing how divisibility works in this context and how the number of divisors determines the final state of each container. By examining the underlying principles of number theory, we can deduce the general rule for which positions will remain open and which will be closed.

The fundamental idea is that each container is toggled based on whether its position number is divisible by a given step number. Initially, all positions are closed. During each step, the containers whose position numbers are divisible by the current step number are toggled. This process continues for all steps, and the challenge is to determine which containers end up open after all steps are completed.

The mathematical proof hinges on the fact that most numbers have an even number of divisors. For example, 12 has divisors 1, 2, 3, 4, 6, and 12. This means that the container at position 12 will be toggled six times, resulting in it being closed at the end. However, for perfect squares, such as 9, 16, or 25, one of the divisors is repeated, making the total number of divisors odd. Since these positions are toggled an odd number of times, they remain open at the end.

Thus, the proof concludes that only positions corresponding to perfect squares will remain open. All other positions, with an even number of divisors, will be toggled back to their initial closed state. This insight not only provides the solution to the puzzle but also highlights the importance of number theory in solving such problems.

How to Visualize the Process of Switching

Understanding the toggling process in this puzzle can be challenging, but visualizing the sequence step by step can make it clearer. One way to think about the process is to imagine each container as a binary state–either open or closed. As each step progresses, containers are toggled based on whether their position is divisible by the current step number. By representing this process visually, we can better understand how the containers change states throughout the process.

A simple approach to visualizing this is by creating a table to track the state of each container. Each row represents a step, and each column represents a container. Initially, all containers start closed. As the steps progress, you toggle the containers whose position numbers are divisible by the current step. This gives a clear, step-by-step overview of how each container changes.

Step	Container 1	Container 2	Container 3	Container 4	Container 5
1	Open	Open	Open	Open	Open
2	Open	Closed	Open	Closed	Open
3	Open	Closed	Closed	Closed	Open
4	Open	Closed	Closed	Open	Open
5	Open	Closed	Closed	Open	Closed

By following this table, you can observe how each step affects the containers. This method helps you understand the toggling process in a structured and visual way. As you progress through the steps, you will see patterns emerge, especially in how positions with an odd number of divisors remain open, while those with an even number of divisors return to their closed state.

Common Mistakes and Misconceptions

When attempting to solve this puzzle, many individuals make common errors due to misunderstandings about how the toggling process works. These mistakes often stem from misinterpreting the rules or overlooking key mathematical principles that dictate the final outcome. Recognizing these pitfalls is crucial for developing a correct understanding of the problem and its solution.

Assuming All Positions Are Toggled the Same Number of Times

A frequent misconception is that all positions are toggled an equal number of times. This is not the case; each position is toggled a number of times based on its divisibility. For example, positions with fewer divisors will be toggled fewer times, while those with more divisors will experience more toggling. This key distinction is essential for identifying which positions remain open at the end.

Overlooking the Role of Perfect Squares

Another common mistake is disregarding the unique role of perfect squares. Many people assume that positions will remain open if they are toggled an odd number of times, but forget that only perfect squares have an odd number of divisors. Recognizing this fact is essential for understanding which positions remain open after all steps are completed.

By addressing these misconceptions and focusing on the fundamental principles, one can gain a clearer and more accurate understanding of how the toggling process works and why certain positions remain open while others are closed. A thorough grasp of these concepts will ensure the correct solution to the puzzle.

Applications of the 100 Locker Problem

The underlying principles of this puzzle have far-reaching applications beyond the specific context in which it is framed. By studying how systems evolve through repeated actions based on divisibility and state changes, we gain insights into various real-world scenarios. These concepts can be applied to problems in fields such as computer science, network security, and even resource management.

Computer Science and Algorithms

In computer science, the idea of toggling elements based on specific criteria is used in sorting algorithms, optimization problems, and dynamic programming. The concept of divisibility plays a key role in the analysis of algorithmic complexity, helping to predict how different operations will scale with increasing input sizes.

• Sorting algorithms: The toggling concept mirrors the way certain sorting algorithms process data, sorting elements by repeatedly checking divisibility or other conditions.
• Optimization problems: The approach of toggling elements in a sequence helps optimize resource allocation by making adjustments at specific intervals.
• Dynamic programming: Similar to the puzzle, dynamic programming often relies on breaking down problems into smaller subproblems, solving each one and building up the solution progressively.

Network Security and Cryptography

The principles from this puzzle also apply to areas like network security and cryptography, where repeated transformations based on certain keys or criteria help maintain system integrity. Just as the positions are toggled based on step divisibility, encryption algorithms often rely on repeated transformations of data at specified intervals to ensure security.

• Cryptographic hashing: The toggling mechanism can be compared to the process of applying cryptographic transformations multiple times to ensure data protection.
• Key distribution: The principles of divisibility and intervals can be seen in systems that rely on periodically changing keys for secure communication.

By exploring these applications, we see how a seemingly simple puzzle can have profound implications in complex fields. Understanding the toggling process and the conditions under which it operates offers valuable insight into real-world problems, making the study of this concept more than just a mathematical exercise.

Real-World Analogies to the Puzzle

The concept behind this puzzle can be applied to various real-life situations where a sequence of actions or changes depends on specific conditions. By drawing parallels to different systems, we can gain a deeper understanding of how such processes unfold and how small adjustments can lead to larger patterns emerging. Below are a few examples of how the principles of this puzzle can be mirrored in everyday scenarios.

Classroom Participation and Group Dynamics

Imagine a classroom where students are asked to participate in activities on certain days. Each student is assigned to a seat, and on certain days, they must switch seats based on specific rules. Over time, the students change their seats repeatedly, and some seats are swapped more frequently than others. This mirrors the way toggling occurs in the puzzle, where actions are applied to certain positions based on divisibility or other criteria.

• Seat-switching: Students who sit in positions that meet specific criteria (like divisibility by a certain number) will change their seats more often.
• Group roles: As with toggling positions, certain students may assume different roles in group activities depending on the rules set at each step.

Voting Systems and Election Results

Another analogy is in voting systems where multiple rounds of voting take place, and candidates are eliminated or promoted based on specific conditions. Each round, certain candidates may receive more attention or support, just as certain positions are toggled more often than others. Over multiple rounds, the pattern of votes and eliminations can lead to a final outcome that is shaped by the earlier steps in the process.

• Ranked voting: In ranked voting systems, candidates are eliminated or chosen based on the divisibility of votes or preferences.
• Progressive selection: The process of moving through elimination rounds can be compared to the toggling of positions, where certain results are only reached after several stages.

Resource Allocation and Scheduling

In resource management or scheduling systems, tasks or resources are allocated over time according to specific rules. Similar to the puzzle, the conditions under which a task is executed may depend on how many times it has been selected previously or how many tasks have been completed before. The final result depends on the number of times each task or resource is toggled or used.

• Task prioritization: Tasks that are selected more frequently are akin to positions being toggled more often in the puzzle.
• Resource usage: Some resources may be allocated more often than others, depending on a set of predefined rules or criteria.

These real-world analogies highlight the applicability of the puzzle’s logic beyond the confines of mathematics. They demonstrate how seemingly simple actions, when repeated under specific conditions, can lead to complex outcomes and patterns. Understanding this dynamic helps to draw connections between abstract mathematical puzzles and practical, everyday situations.