AP Statistics Chapter 6 Homework Answers

The sixth section of the course explores essential methods and techniques for solving complex problems in the field of data analysis. Mastery of these topics is crucial for building a strong foundation in interpreting numerical information and making informed decisions based on statistical principles.

In this guide, we will break down the key concepts and walk through practical examples, ensuring that each step of the process is clear and understandable. Whether you’re tackling probability challenges or refining your understanding of distributions, this resource will help you navigate the material with confidence.

AP Course Section 6 Solutions

This section focuses on applying key concepts and solving a variety of challenges related to data analysis. By understanding and working through these problems, you’ll gain the skills needed to analyze and interpret complex numerical patterns and distributions effectively.

In the following table, we’ve compiled step-by-step solutions to commonly encountered problems. Each solution provides a clear breakdown of how to approach and solve the questions, allowing you to strengthen your grasp of the material.

Problem	Solution Steps	Explanation
Probability Calculation	1. Identify the event of interest 2. Apply probability rules 3. Simplify the expression	Breaking down complex probability problems into smaller, manageable parts ensures accuracy and clarity.
Distribution Interpretation	1. Define the type of distribution 2. Calculate mean and standard deviation 3. Analyze distribution shape	Understanding the key properties of a distribution allows for proper interpretation and comparison with other datasets.
Hypothesis Testing	1. State the null and alternative hypothesis 2. Determine the significance level 3. Calculate test statistic and p-value	Using clear steps in hypothesis testing ensures correct conclusions are drawn from the data.

Understanding Key Concepts in Section 6

This section introduces several fundamental principles essential for working with data and analyzing patterns. It covers techniques that allow you to make sense of numerical information, whether you’re dealing with probabilities, distributions, or other statistical models. A strong understanding of these concepts is crucial for solving more complex problems and drawing meaningful conclusions from data.

By grasping the key ideas presented here, you’ll develop a deeper insight into how data behaves, how to interpret various measures, and how to apply these methods to solve practical problems. These concepts form the foundation of more advanced techniques used in analyzing datasets and conducting inference.

Common Problems in AP Stats Section 6

Throughout this section, students often encounter several recurring challenges when working with data analysis methods. These problems typically involve misunderstanding key concepts, misapplying formulas, or failing to correctly interpret results. Recognizing these common issues early on can help avoid confusion and improve problem-solving skills.

One of the most frequent obstacles is accurately interpreting the relationships between variables, especially when dealing with probability models or distributions. Additionally, students often struggle with applying the right techniques for hypothesis testing or drawing inferences from sample data. Identifying and addressing these difficulties is crucial for mastering the material and building confidence in handling complex tasks.

Step-by-Step Guide to Solving Exercises

In this section, we will walk through the process of solving problems with clear, structured steps. Breaking down each exercise into manageable parts makes it easier to understand the logic behind the solution and helps ensure accuracy. By following this methodical approach, you can tackle even the most complex problems with confidence.

1. Understand the Problem

The first step in solving any problem is to carefully read and comprehend the given information. Identify the key variables and determine what is being asked. Take note of any specific conditions or constraints that may affect the solution. This foundational understanding will guide the entire process.

2. Apply Relevant Formulas

Once you understand the problem, apply the appropriate formulas or techniques required to find the solution. Ensure that you are using the correct formula for the type of problem you’re solving. For example, when working with distributions, it is crucial to know the formula for the mean, variance, or standard deviation, depending on the context.

Tip: Always double-check your work at each step to avoid small mistakes that could lead to incorrect results.

How to Interpret Statistical Data Effectively

Interpreting data correctly is essential for making informed decisions based on numerical information. Understanding how to read and analyze data allows you to draw accurate conclusions and avoid misinterpretations. In this section, we’ll discuss key techniques to improve your ability to interpret data with clarity and precision.

Understanding Data Distribution

One of the most important skills is recognizing the distribution of data. This helps in identifying patterns, trends, and potential outliers that may influence the results. Knowing whether the data follows a normal distribution or another form allows for better application of statistical techniques and models.

Evaluating Measures of Central Tendency

Another crucial aspect is understanding measures such as the mean, median, and mode. These metrics provide insight into the center of a dataset and help in comparing different sets of information. Depending on the nature of the data, each measure offers a different perspective on the overall distribution.

Measure	Use Case	Interpretation
Mean	Used for symmetrical distributions	Represents the average value, but sensitive to extreme values
Median	Used for skewed distributions	Represents the middle value, more resistant to outliers
Mode	Used to identify the most frequent value	Shows the most common value in the dataset

Tips for Approaching Probability Problems

When faced with probability problems, a systematic approach is essential for finding accurate solutions. These types of questions often involve complex reasoning, so breaking them down into smaller, manageable steps can simplify the process and help ensure clarity. Understanding the rules and techniques behind probability calculations is key to solving problems effectively.

1. Understand the Problem

Before jumping into calculations, take the time to fully understand the scenario. Identify what is being asked and what information is provided. This ensures that you’re applying the correct concepts to the right elements of the problem.

2. Apply Key Probability Rules

Familiarize yourself with fundamental probability rules, such as addition, multiplication, and conditional probability. These rules will guide you in solving the problem by simplifying complex scenarios.

• Addition Rule: Used when events are mutually exclusive.
• Multiplication Rule: Used for independent events.
• Conditional Probability: When the probability of an event depends on the outcome of a prior event.

3. Use Visual Aids

Often, drawing a diagram or using a probability tree can help visualize relationships between events. This is especially useful in cases of conditional probability or when dealing with multiple events.

4. Double-Check Your Calculations

Probability problems can be tricky, and it’s easy to overlook details. After solving, review your steps and check for common errors such as misapplying a formula or overlooking an assumption.

Mastering the Normal Distribution

Understanding the normal distribution is a critical skill for analyzing data in various fields. It is one of the most commonly used distributions in probability and data analysis, as it represents the behavior of many natural phenomena. Mastering this concept allows you to interpret data patterns and make predictions with greater accuracy.

The normal distribution is symmetrical, with the majority of values clustered around the mean. Its shape is often referred to as a “bell curve,” and it is characterized by two key parameters: the mean (which determines the center) and the standard deviation (which measures the spread of the data). A good grasp of these concepts will help you solve problems involving probabilities, percentiles, and other related calculations.

To effectively work with the normal distribution, you need to become familiar with the Z-score, which standardizes data and allows you to compare values from different distributions. Additionally, knowing how to use standard normal tables or statistical software will enable you to find probabilities and make informed decisions based on data.

Understanding Variance and Standard Deviation

Variance and standard deviation are two key measures that help us understand the spread or dispersion of data points in a dataset. They provide insight into how much individual values differ from the mean, allowing us to assess the consistency or variability within the data. These concepts are foundational in data analysis, as they offer a clear picture of the overall distribution.

Variance is a measure of how far each data point in a set is from the mean, while standard deviation is simply the square root of variance. Both metrics are used to quantify the degree of variation in a dataset, with the standard deviation offering a more interpretable measure due to its same units as the original data.

Measure	Formula	Interpretation
Variance	?? = ?(x – ?)? / N	Measures the average squared deviation from the mean. A higher variance indicates greater spread.
Standard Deviation	? = v(?(x – ?)? / N)	Measures the average distance from the mean. A higher value indicates more variability in the data.

Both variance and standard deviation play a critical role in understanding how data behaves, particularly when comparing different datasets or assessing the reliability of a given set of values. The lower the variance or standard deviation, the more tightly packed the data is around the mean. Conversely, higher values indicate a wider spread, suggesting more variability or uncertainty in the data.

Analyzing Statistical Inferences in AP Stats

When dealing with data, drawing valid conclusions is essential. Statistical inferences allow us to make predictions and decisions based on sample data. Understanding how to analyze these inferences is crucial, as it helps assess the reliability and validity of conclusions drawn from a sample, rather than the entire population. In this section, we will explore key concepts related to making informed judgments from sample data.

Key Concepts in Statistical Inferences

There are several important aspects to consider when evaluating inferences drawn from data:

• Confidence Intervals: A range of values that likely contain the population parameter, giving us an idea of the accuracy of our estimate.
• Hypothesis Testing: A method used to assess whether there is enough evidence to support a claim about a population parameter.
• P-Values: A measure that helps determine the strength of the evidence against the null hypothesis.
• Sampling Error: The difference between the sample result and the true population parameter, which can impact the accuracy of the inference.

Steps in Analyzing Inferences

To properly analyze statistical inferences, follow these steps:

1. Formulate a hypothesis: Define what you are testing or estimating. This will guide the entire analysis process.
2. Collect and analyze the data: Ensure the sample data is appropriate for the hypothesis and calculate necessary statistics.
3. Assess the confidence: Calculate confidence intervals or p-values to determine the level of certainty about the conclusion.
4. Make a decision: Based on the results, decide whether to accept or reject the hypothesis, keeping in mind the possibility of error.

By following these principles and steps, you can effectively analyze inferences in statistical problems, ensuring that your conclusions are well-supported by the data. Understanding how to apply these concepts is essential for accurate interpretation and decision-making in data analysis.

How to Approach Hypothesis Testing

Hypothesis testing is a method used to make decisions or draw conclusions about a population based on sample data. The goal is to determine whether there is enough evidence to support a particular claim or assumption. A structured approach is essential to ensure that the results are reliable and valid. This process involves clearly stating a hypothesis, collecting appropriate data, and using statistical methods to test the hypothesis.

Steps in Hypothesis Testing

To conduct a hypothesis test effectively, follow these key steps:

• Define the null and alternative hypotheses: The null hypothesis usually represents the idea of no effect or no difference, while the alternative hypothesis represents the claim you want to test.
• Choose the significance level: The significance level (?) indicates the threshold for rejecting the null hypothesis, typically set at 0.05, 0.01, or 0.10.
• Collect and analyze the data: Gather sample data and calculate the relevant test statistic (e.g., t-test, z-test) based on the type of data and hypothesis.
• Calculate the p-value: The p-value measures the strength of the evidence against the null hypothesis. A smaller p-value indicates stronger evidence against it.
• Make a decision: Compare the p-value to the significance level. If the p-value is less than ?, reject the null hypothesis; otherwise, fail to reject it.

Interpreting Results

Once the hypothesis test is completed, it’s important to interpret the results carefully. If the null hypothesis is rejected, it suggests that the sample provides enough evidence to support the alternative hypothesis. If the null hypothesis is not rejected, there is insufficient evidence to conclude that the claim is true. Always consider the context of the data and the potential for errors when making conclusions.

Solving Regression and Correlation Problems

Understanding the relationship between two variables is a key aspect of data analysis. Regression and correlation are methods used to explore these relationships, allowing us to make predictions and assess the strength of associations between variables. By analyzing the patterns in the data, we can identify trends and draw meaningful conclusions that inform decision-making.

Steps for Solving Regression Problems

To solve regression problems, it’s important to follow a structured approach. Here are the key steps to consider:

1. Identify the variables: Determine the dependent (response) variable and the independent (predictor) variable.
2. Plot the data: Create a scatterplot to visually assess the relationship between the variables.
3. Calculate the regression equation: Use the least squares method to calculate the equation of the line (e.g., y = mx + b) that best fits the data.
4. Interpret the results: Analyze the slope and intercept of the regression line to understand how the predictor variable influences the response variable.
5. Make predictions: Use the regression equation to predict the value of the dependent variable based on the independent variable.

Solving Correlation Problems

Correlation measures the strength and direction of the relationship between two variables. To solve correlation problems, follow these steps:

1. Calculate the correlation coefficient: The correlation coefficient (r) indicates the strength of the linear relationship between the variables. Values closer to 1 or -1 suggest a stronger relationship.
2. Interpret the direction: A positive correlation means that as one variable increases, the other also increases, while a negative correlation indicates the opposite.
3. Assess the strength: The closer the correlation coefficient is to 1 or -1, the stronger the linear relationship. A value close to 0 suggests little or no linear relationship.
4. Check for causality: Keep in mind that correlation does not imply causation. Even if two variables are correlated, it does not mean that one causes the other.

By following these steps for both regression and correlation, you can analyze the relationship between variables effectively. Understanding the underlying trends in the data enables you to make more informed decisions and predictions based on the observed patterns.

Interpreting Confidence Intervals in Stats

Confidence intervals provide a range of values within which we expect the true population parameter to lie, based on sample data. These intervals give us a sense of uncertainty and reliability in our estimates, allowing us to assess how confident we can be in our findings. Interpreting these intervals correctly is essential for making informed conclusions and decisions.

Understanding the Concept of Confidence Levels

Confidence intervals are typically associated with a confidence level, such as 95% or 99%. The confidence level represents the proportion of times that the interval would contain the true population parameter if the same sampling procedure were repeated numerous times. A higher confidence level provides a wider interval, reflecting greater uncertainty about the exact value.

How to Interpret a Confidence Interval

To interpret a confidence interval, consider the following points:

• Interval range: The confidence interval gives a range of plausible values for the population parameter. For example, a 95% confidence interval of [10, 15] means that we are 95% confident that the true value lies between 10 and 15.
• Margin of error: The width of the interval is determined by the margin of error, which depends on the sample size and variability of the data. A smaller margin of error suggests a more precise estimate.
• Confidence level: A higher confidence level increases the interval’s width, reflecting a greater level of certainty about the estimate. For instance, a 99% confidence interval will be wider than a 95% interval.
• Interpretation of the interval: If the interval includes a value of interest, such as zero or another benchmark, it may indicate that there is insufficient evidence to suggest a significant effect or difference.

Correctly interpreting confidence intervals allows for more nuanced conclusions, helping us to understand the reliability of estimates and the degree of uncertainty in our results. By recognizing the implications of these intervals, you can make more informed decisions based on data analysis.

Identifying Errors in Statistical Calculations

In any data analysis process, errors in calculations can significantly affect the results and lead to incorrect conclusions. Identifying these errors is crucial for ensuring the accuracy of the analysis. Understanding the common types of mistakes and how to avoid them can help prevent inaccurate results and improve the reliability of your findings.

Common Types of Errors

Errors can arise at various stages of data analysis, from data collection to calculation. Below are some common types of mistakes that often occur:

Error Type	Description
Data Entry Mistakes	Incorrect data input or transcription errors can skew results and lead to faulty analysis.
Calculation Errors	Misapplication of formulas or computational errors can result in incorrect values for key metrics like averages or standard deviations.
Sampling Bias	Using a non-representative sample can lead to incorrect generalizations about the population being studied.
Misinterpretation of Results	Incorrectly interpreting statistical outputs or overestimating the significance of findings can lead to erroneous conclusions.

How to Avoid Errors in Calculations

To minimize errors in your analysis, consider the following strategies:

• Double-check data inputs: Ensure that the data is entered correctly and verify values before proceeding with calculations.
• Use reliable software: Use tools and software that are known for accuracy and have built-in error-checking functions.
• Validate assumptions: Make sure the assumptions underlying the methods used are appropriate for your data.
• Cross-check calculations: Perform calculations by hand or use multiple methods to verify results, ensuring consistency across different approaches.
• Consult reliable resources: Refer to textbooks, guides, or experts to confirm the proper application of formulas and interpretation of results.

By recognizing common errors and implementing strategies to avoid them, you can significantly improve the accuracy of your data analysis and draw more reliable conclusions from your findings.

Using Graphs to Solve Problems Efficiently

Graphs are powerful tools for visualizing data and relationships, making complex problems easier to understand and solve. They provide an intuitive way to spot patterns, trends, and outliers that might be difficult to identify through raw numbers alone. By incorporating graphs into your problem-solving process, you can save time and improve accuracy.

Types of Graphs for Problem Solving

Different types of graphs are useful for different kinds of problems. Here are some commonly used graphs that can help in various scenarios:

• Bar Graphs: Ideal for comparing quantities across different categories. They allow for easy visualization of differences and trends.
• Line Graphs: Useful for tracking changes over time, making it easier to identify patterns or trends in a continuous dataset.
• Scatter Plots: Best for showing the relationship between two variables, helping to detect correlations or outliers.
• Histograms: Effective for displaying the distribution of data and understanding the frequency of values within specific ranges.
• Pie Charts: Helpful for visualizing proportions and percentages within a whole, making it easier to compare parts of a dataset.

How Graphs Improve Problem Solving

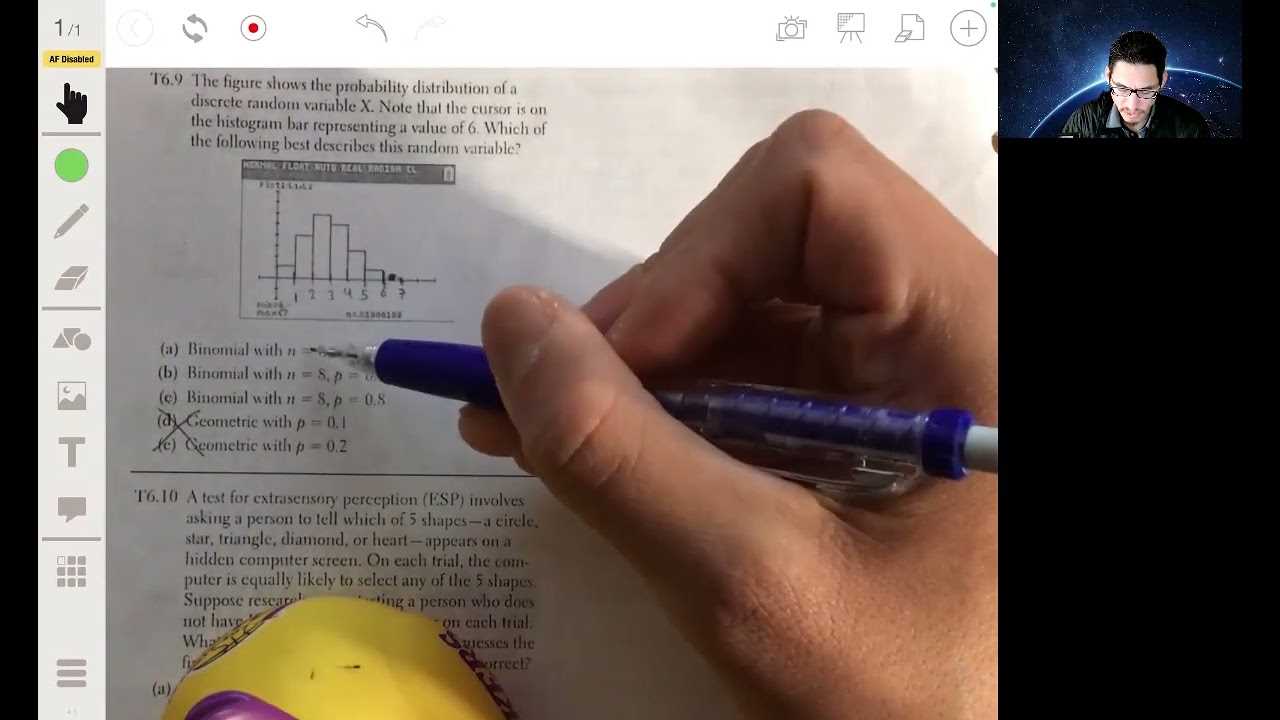
Graphs can significantly enhance problem-solving in several ways:

• Clarifying Complex Information: They simplify complicated data, making it easier to grasp key concepts and relationships at a glance.
• Identifying Trends Quickly: Graphs highlight trends, allowing for rapid identification of patterns that may require more time to spot through calculations alone.
• Improving Decision Making: By visualizing potential outcomes, graphs enable you to make informed decisions based on data-driven insights.
• Supporting Hypotheses: Graphs provide a visual representation of your hypotheses, helping to confirm or challenge assumptions with clear, concrete evidence.

Incorporating graphs into your problem-solving strategy can lead to more efficient analysis and clearer conclusions. Whether you’re comparing data points, identifying relationships, or visualizing trends, graphs are indispensable for making the problem-solving process more efficient and effective.

Strategies for Success in AP Statistics

Achieving success in this subject requires a blend of strong conceptual understanding, effective time management, and strategic problem-solving. Developing a methodical approach to mastering the material will not only help you navigate complex tasks but also enable you to approach them with confidence. Here are some essential strategies to ensure you excel in your studies.

Mastering Key Concepts

The foundation of success lies in understanding the core principles. Rather than memorizing formulas, focus on understanding the logic behind each concept. Here are a few key tips:

• Review fundamentals regularly: Make sure you have a clear grasp of basic principles like probability, data interpretation, and graph analysis before diving into more complex topics.
• Focus on real-world applications: Relating concepts to practical examples helps solidify your understanding and gives context to abstract ideas.
• Ask questions: If something is unclear, don’t hesitate to ask for clarification. Understanding the “why” behind every problem is essential for long-term success.

Effective Study Habits

Studying for this subject involves more than simply reading notes or watching videos. To maximize your success, implement these strategies:

• Practice consistently: The more problems you solve, the better your skills will become. Set aside time each day for focused practice to improve both speed and accuracy.
• Break down problems: Tackle problems step by step. Start with what’s known, identify what’s being asked, and methodically apply concepts to find solutions.
• Utilize study groups: Collaborating with peers can help reinforce concepts and expose you to different problem-solving methods. You’ll also get the chance to explain concepts, which strengthens your own understanding.

By mastering key concepts and adopting disciplined study habits, you will develop the confidence and skills necessary to succeed in this subject. Consistency, practice, and a clear understanding of the material are the pillars of success.

Preparing for the AP Exam

Successfully preparing for the AP exam requires not just understanding the material but also developing effective strategies for tackling a wide variety of problems. It’s important to approach your studies systematically and ensure you’re familiar with the key concepts and techniques that will be tested. By focusing on areas that are frequently assessed, you can improve your chances of performing well on the exam. Here are some tips to help you get ready:

Review Key Concepts and Formulas

Start by revisiting the core concepts and essential formulas. Understanding the fundamental principles behind each topic will help you apply the correct methods during the exam. Key areas to focus on include:

• Data analysis techniques
• Probability rules
• Interpretation of graphs and charts
• Hypothesis testing and regression analysis

Practice with Real-World Problems

Another critical aspect of preparing is practicing with a variety of problems, especially those that closely resemble the types of questions you’ll encounter on the exam. Focus on:

• Timed practice tests to simulate exam conditions
• Identifying patterns in questions and solutions
• Refining problem-solving techniques under pressure

By combining a strong understanding of the material with regular practice, you’ll be well-equipped to succeed on the test. Stay organized, manage your time effectively, and remember that consistency is key to mastering the content and building confidence for exam day.