Regents Exam A2 S7 Exponential Regression Answer Key

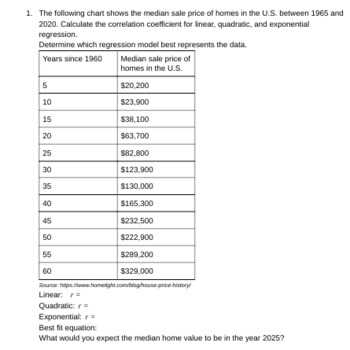
In this section, we focus on understanding a critical part of mathematical assessments that deals with modeling real-world data patterns. This involves applying advanced methods to identify relationships between variables and interpret results. By mastering these techniques, you can efficiently tackle related problems and enhance your problem-solving skills.

The key to success lies in grasping the underlying principles and knowing how to manipulate data to achieve meaningful conclusions. Students often face challenges in this area, but with careful study and practice, the concepts become clearer and more manageable. Familiarity with the process will allow you to approach similar tasks with confidence and precision.

Understanding Exponential Regression in Regents Exam

In mathematical assessments, one of the essential skills is the ability to model relationships between variables that grow or decay at a consistent rate. These models help to predict future trends based on past data. Understanding how to identify and work with such relationships is crucial for solving real-world problems that involve population growth, finance, or scientific phenomena.

The process involves fitting a curve to data points that follow a particular pattern, often represented by a mathematical function. Students must learn how to recognize when this type of relationship exists and how to apply the appropriate techniques to determine the best-fitting model. With practice, you will be able to confidently analyze and interpret the results, ensuring accurate predictions and conclusions.

Key Concepts of Exponential Functions

When studying mathematical models involving growth or decay, it’s essential to understand the behavior of certain functions. These functions describe situations where the rate of change is proportional to the current value, leading to patterns that accelerate or decelerate over time. Familiarity with these functions is crucial for interpreting a wide range of real-world phenomena.

Some key features of these functions include:

• Base Value: The constant factor that influences the rate of growth or decline.
• Rate of Change: The rate at which the quantity increases or decreases, often represented as a percentage.
• Initial Value: The starting point or the value of the function when the time variable is zero.
• Asymptotes: A line that the graph of the function approaches but never reaches, often representing a limiting value.

Understanding these principles will help you effectively analyze data and recognize patterns that follow this type of mathematical relationship. Mastery of these concepts allows for accurate modeling and prediction of future outcomes based on existing trends.

How to Approach Regents A2 S7 Questions

When tackling problems that involve identifying patterns in data, it’s important to have a structured approach. These types of tasks often require analyzing a set of numbers or a graph and applying mathematical concepts to find relationships. Knowing the proper steps to take can make the process more efficient and ensure accuracy in your results.

Step 1: Analyze the Given Data

The first step in solving any related problem is to carefully examine the data provided. Look for trends, whether the values are increasing, decreasing, or remaining constant. Understanding the overall pattern will guide you toward selecting the correct method for analysis. Pay attention to the scale of the data and any key variables that could influence the results.

Step 2: Choose the Right Method

Once you’ve identified the pattern in the data, decide on the appropriate approach to model the relationship. This might involve using specific formulas, graphing tools, or statistical methods. The method you choose will depend on the behavior of the data–whether it is growing or declining at a constant rate, for example. With the right tools, you can find the best fit and make reliable predictions based on your analysis.

Step-by-Step Guide to Exponential Regression

When tasked with modeling data that exhibits a growth or decay pattern, it’s essential to follow a clear, methodical approach. This guide will walk you through the process of determining the best-fitting model for such data, ensuring accurate predictions and meaningful analysis. By following these steps, you’ll be able to effectively handle problems that require identifying trends based on past observations.

Step 1: Gather and Organize Your Data

The first step is to collect all the relevant data points and organize them in a table or a graph. It’s important to have both the independent and dependent variables clearly labeled. This allows you to see the relationship between the two variables and prepares you to apply the appropriate methods. Ensure that your data is accurate and consistent before proceeding.

Step 2: Plot the Data and Identify the Pattern

Once you have the data, plot it on a graph to visually identify the type of relationship between the variables. If the data shows an increasing or decreasing trend that seems to accelerate or decelerate, it may be a sign that a specific type of model will fit best. Look for a curve in the graph that rises or falls steeply as opposed to a straight line. This visual inspection will guide you toward selecting the correct model.

After identifying the pattern, you can proceed to calculate the necessary parameters and finalize the model. With each step, ensure you are cross-checking the results for accuracy and consistency.

Interpreting Data with Exponential Models

When working with data that follows a particular growth or decay pattern, it’s essential to correctly interpret the results and understand the implications. These models help in making predictions and understanding the nature of change over time. By examining the data within the framework of such models, you can gain valuable insights into future trends and behaviors.

Once you have fit a model to the data, the next step is to analyze the results. The key parameters–such as the rate of change and initial values–play a significant role in determining how well the model represents the real-world situation. It’s important to understand the meaning of each parameter and how it affects the overall trend.

Parameter	Description	Impact on the Model
Initial Value	The starting value when time is zero	Determines where the curve begins on the graph
Growth Rate	The rate at which the value increases	Controls how steeply the curve rises over time
Decay Rate	The rate at which the value decreases	Determines how quickly the value declines
Asymptote	The horizontal line the graph approaches	Represents a limiting value that the model will never cross

Interpreting the results accurately requires a strong understanding of how these parameters interact. This allows you to assess the reliability of the model and use it effectively to make informed predictions.

Common Mistakes in Exponential Regression

When dealing with problems that involve modeling data patterns, it’s easy to make mistakes that can affect the accuracy of your results. These errors often arise from misunderstandings about the behavior of the data or improper application of mathematical techniques. Recognizing and avoiding common mistakes can greatly improve the reliability of your models and your overall problem-solving skills.

Some frequent errors include:

• Misinterpreting the Data Trend: Failing to recognize when data follows a consistent growth or decay pattern can lead to choosing the wrong modeling approach.
• Incorrectly Identifying the Best Fit: Trying to force a linear model or another type of curve when the data clearly follows a different pattern can lead to misleading results.
• Forgetting to Check for Outliers: Data points that are far removed from the general trend can distort the fit and lead to inaccurate predictions.
• Overlooking the Asymptote: In some cases, the model might approach a certain value but never reach it. Ignoring this limitation can lead to unrealistic conclusions.
• Not Validating the Model: Failing to check the model’s accuracy by comparing it against known data or by using residual plots can result in poor predictions.

By being mindful of these common mistakes, you can approach modeling problems with greater confidence and ensure that your conclusions are based on sound mathematical principles. Regular practice and attention to detail are key to improving accuracy and avoiding errors.

Using Technology for Exponential Regression

In today’s world, technology plays a crucial role in simplifying complex calculations and helping analyze data efficiently. Tools like graphing calculators, spreadsheets, and specialized software allow for quick and accurate modeling of data, enabling users to identify patterns and make predictions with ease. Understanding how to use these tools effectively is essential for solving problems involving growth or decay trends.

Step 1: Inputting Data into Software

The first step when using technology for this type of analysis is to input your data correctly. Most software programs allow you to enter data points into a table or spreadsheet format. Once the data is in place, the software can quickly generate a graph, helping you visually assess the pattern of change.

Step 2: Using Built-in Functions for Modeling

Many tools come with built-in functions that automatically perform the necessary calculations for curve fitting. These functions calculate the parameters of the model, such as the rate of change and the initial value. With just a few clicks, you can obtain a precise model that represents the data, saving time and minimizing errors. Additionally, most software will provide a graphical representation of the model, making it easier to visualize the relationship between variables.

By leveraging technology, you can streamline the process of analyzing and interpreting data, allowing you to focus on understanding the results and making informed decisions based on your findings.

How to Solve for Regression Coefficients

When working with data that follows a particular trend, it’s essential to determine the key parameters that define the relationship between variables. The coefficients of a mathematical model are the values that describe how one variable influences another. Solving for these coefficients allows you to create a precise model, enabling accurate predictions based on the observed data.

Step 1: Understand the Model Structure

The first step is to recognize the general form of the model you’re working with. Typically, the model is written as a formula that includes one or more coefficients. For example, in many cases, the model may take the form of an equation like:

• y = a * b^x, where a is the initial value and b is the growth or decay factor.
• y = a * e^(bx), where a is the starting value and b is the rate of change.

Step 2: Use Technology or Manual Methods

Once you understand the structure, you can solve for the coefficients using either manual calculation methods or technological tools.

• Manual Calculation: This involves using statistical methods such as least squares fitting to calculate the values of the coefficients. It requires solving a system of equations or using logarithmic transformations in some cases.
• Using Technology: Many tools, like graphing calculators or software programs, can automatically compute these coefficients by fitting the data to the model. Simply input your data, and the tool will provide the values for the coefficients.

By solving for the coefficients, you’ll be able to describe the relationship between variables in a precise mathematical way, allowing for predictions and further analysis.

Real-World Applications of Exponential Regression

Mathematical models that describe growth or decay are widely used in various fields to analyze real-world phenomena. By fitting data to these models, we can make predictions and better understand the behaviors of complex systems. From biology to finance, these models are invaluable tools in solving practical problems and making informed decisions.

Some of the common areas where these models are applied include:

• Population Growth: In biology and ecology, growth patterns of species or populations often follow specific trends. Using these models helps estimate future population sizes, aiding in conservation efforts and resource management.
• Financial Analysis: In economics and finance, these models are used to understand the growth of investments, interest rates, or asset depreciation. They allow investors to forecast future values and assess the risk and return of investments.
• Radioactive Decay: In physics and chemistry, the decay of radioactive substances follows predictable patterns. These models help scientists estimate the remaining amount of a substance over time, which is critical in fields like nuclear energy and medicine.
• Medicine and Health: These models are used to track the spread of diseases or the effectiveness of treatments. For example, understanding how a virus spreads can guide public health responses, while predicting the effects of a drug can help improve patient care.
• Technology and Innovation: In the tech industry, the adoption of new technologies often follows an exponential curve. By modeling this growth, companies can anticipate market demand and plan their product development strategies accordingly.

These examples demonstrate the wide range of fields where growth and decay models can provide valuable insights. By applying these mathematical tools, professionals can make more accurate predictions and informed decisions, benefiting society and industries alike.

Understanding the Answer Key for A2 S7

When solving problems involving complex mathematical models, it’s crucial to understand how to interpret the provided solutions. The key serves as a guide to the correct approach, outlining the steps and methods used to solve each problem. By reviewing the answer key, learners can gain insight into the logical processes and calculations involved, ensuring they can apply similar techniques in future problems.

The key typically includes several key components:

• Step-by-step breakdown: A detailed explanation of each calculation or method used, showing how to progress from one stage to the next.
• Clarifications of common pitfalls: Tips on how to avoid typical mistakes that might arise while solving these types of problems.
• Final results: The completed solution, showing the correct values for all variables involved in the problem.

By carefully analyzing the answer key, students not only confirm their results but also reinforce their understanding of the underlying concepts and methods. This makes the key an essential tool for learning and mastering complex mathematical concepts.

Reviewing Sample Problems and Solutions

Reviewing sample problems and their corresponding solutions is a critical practice for mastering any mathematical concept. By examining how problems are approached and solved step by step, learners can develop a deeper understanding of the methods and techniques used. This process not only reinforces the knowledge gained but also highlights the reasoning behind each decision made during the solution process.

When reviewing sample problems, focus on the following aspects:

• Understanding the Problem: Carefully analyze the given information and determine what is being asked. This step ensures that you know the goal before proceeding with any calculations.
• Identifying Key Concepts: Recognize the mathematical principles or formulas that apply to the problem. This might involve identifying patterns or relationships between variables.
• Step-by-step Approach: Follow the solution’s steps closely. Pay attention to how each calculation is made and why certain methods are chosen over others. This helps clarify how to apply these techniques in future problems.

As you review, take note of any mistakes or areas of confusion. Understanding where errors might occur and how they are corrected is an essential part of improving problem-solving skills. By practicing this method regularly, you will be better prepared to tackle similar challenges with confidence and accuracy.

Why Exponential Regression Matters in Algebra

Understanding certain mathematical models is essential in algebra as they provide a framework for analyzing real-world data. One such model focuses on the growth and decay patterns that can be represented with specific equations. These models allow students to explore the relationships between variables and learn how to predict outcomes based on trends. Grasping these concepts not only enhances problem-solving skills but also develops a deeper understanding of how math can be applied in various fields.

In algebra, this type of modeling is particularly important for several reasons:

• Real-World Applications: Many natural and societal processes, such as population growth or the spread of diseases, follow predictable patterns that can be represented algebraically. Understanding these patterns helps us make informed predictions about the future.
• Critical Thinking Development: The process of fitting data to a model requires critical thinking and the ability to analyze trends. By learning to apply these techniques, students sharpen their analytical skills and develop a structured approach to problem-solving.
• Foundation for Advanced Studies: Mastery of these methods provides a strong foundation for more advanced mathematical topics, such as calculus or statistics, where these models are frequently applied to more complex scenarios.

By studying and applying these concepts in algebra, students gain the tools needed to not only solve academic problems but also to understand and address challenges in everyday life. This ability to model and predict is a powerful skill in many fields, including science, economics, and engineering.

Preparing for Regents Exam A2 Section 7

Preparing for a mathematical assessment can be a daunting task, especially when it involves complex concepts that require both theoretical understanding and practical application. The key to success lies in breaking down the material into manageable sections and practicing regularly. By focusing on specific problem types and familiarizing yourself with the methods required to solve them, you can build both confidence and competence for the upcoming challenge.

Focus Areas for Preparation

To effectively prepare for Section 7, focus on the following areas:

• Understanding the Core Concepts: Begin by reviewing the fundamental principles that govern the problem-solving strategies in this section. This includes grasping the relationships between variables and how to apply the appropriate formulas.
• Practice with Sample Problems: Work through a variety of practice problems that reflect the types of questions you might encounter. Pay close attention to the methods used in each solution and make sure you understand each step.
• Mastering Graphing Techniques: Many problems in this section involve graphing data and interpreting patterns. Ensure that you are comfortable with plotting data points and identifying trends, as this skill will be essential for solving problems accurately.

Effective Study Strategies

In addition to focusing on the key topics, consider these strategies for optimizing your study sessions:

• Time Management: Create a study schedule that allows for consistent review without overwhelming yourself. Break down your study sessions into shorter, focused intervals to maintain concentration.
• Seek Help When Needed: If you encounter difficulties with certain topics, don’t hesitate to ask for assistance from teachers, tutors, or online resources. Clarifying doubts early on will prevent confusion later.
• Review and Repeat: Regularly revisit the concepts you’ve studied to reinforce your understanding. Practice makes perfect, so the more problems you solve, the more confident you’ll become.

By applying these strategies and committing to consistent practice, you will be well-prepared to tackle the challenges in Section 7 and perform confidently during your assessment.

Tips for Effective Study of Exponential Regression

Mastering the process of analyzing data and fitting models to it requires understanding the underlying patterns and applying the right techniques to solve problems accurately. Whether you are tackling a mathematical challenge or working through applied scenarios, effective study habits are crucial. Below are some practical tips to help streamline your preparation and enhance your understanding of these types of problems.

Essential Study Tips

• Understand the Concepts: Before diving into calculations, make sure you understand the core ideas behind the problem. Grasping the concepts of how data behaves and how to fit it to a model is essential for success.
• Work on Basic Skills: Ensure that you are comfortable with foundational skills, such as manipulating equations, working with graphs, and recognizing patterns in data. These skills will form the basis for more complex tasks.
• Break Down Complex Problems: When you come across challenging problems, break them down into smaller, more manageable parts. Tackling each part individually will help you understand the overall problem more clearly.

Utilizing Tools and Resources

Using technology and other resources can significantly enhance your learning experience:

• Use Graphing Calculators: Many tools can assist you in visualizing data and fitting models. Familiarize yourself with a graphing calculator to practice plotting data and interpreting results.
• Review Sample Problems: Reviewing worked examples can help solidify your understanding of problem-solving techniques. Pay attention to each step and try to understand why each operation is performed.
• Study with Peers: Collaborating with classmates or study groups can expose you to different perspectives and strategies for solving problems. Explaining concepts to others is also a great way to reinforce your knowledge.

Organizing Your Study Sessions

Effective study sessions are well-organized and focused. Here’s how to structure your time:

Study Focus	Time Allocation
Concept Review	30 minutes
Practice Problems	45 minutes
Solution Analysis	15 minutes
Self-Assessment	30 minutes

By dividing your study time into focused intervals, you can stay organized and ensure that all aspects of the material are covered. Regularly assess your understanding and revisit difficult concepts to reinforce learning.

By following these tips and maintaining consistent practice, you will be well-equipped to tackle problems with confidence and mastery.

Interpreting Graphs in Exponential Regression

Graphs are a powerful tool for visualizing data and understanding underlying patterns. In many mathematical contexts, particularly when dealing with data sets that change rapidly, interpreting graphs accurately is essential. Being able to extract meaningful information from these graphs can guide you in making predictions, analyzing trends, and understanding the behavior of the data over time.

Key Features to Look For

When analyzing graphs in this context, there are several key features that can provide valuable insights:

• Growth or Decay Patterns: One of the first things to notice is whether the graph shows a growth or decay pattern. If the graph rises sharply, it indicates rapid growth, while a steep decline suggests rapid decay.
• Asymptotes: Many graphs of this type approach a horizontal line as they progress, which is known as an asymptote. This indicates that, although the values may increase or decrease, they will never reach a certain limit.
• Rate of Change: Observing the steepness of the curve can give an indication of the rate of change. A steeper curve suggests a faster rate, while a more gradual curve indicates a slower rate of change.

Understanding the Data Points

Each point on the graph represents a specific data value that is part of the overall trend. To interpret these points effectively:

• Identify the Coordinates: Each point has an x and y coordinate, where the x value typically represents time or another independent variable, and the y value represents the dependent variable.
• Analyze the Distribution: Look for clustering or spread in the data points. A uniform spread suggests a steady trend, while clusters can indicate specific intervals of rapid change.
• Check for Outliers: Outliers are data points that deviate significantly from the rest of the data. These should be carefully examined to determine if they represent errors or important anomalies in the data.

By focusing on these features, you can gain a deeper understanding of the data’s behavior and make informed decisions based on the visual representation of the information.

Common Patterns in Exponential Data

When analyzing data that changes over time, certain patterns often emerge. These patterns can help identify whether the data follows a particular type of growth or decline. By recognizing these patterns, you can make predictions about future values and understand the overall trend in the data more clearly.

Below are some common patterns observed in such data sets:

Pattern	Description	Example
Rapid Growth	Increases sharply over time, typically seen in populations or investments with high returns.	Doubling of population in a short period
Rapid Decay	Decreases sharply, often seen in the decay of radioactive materials or depreciation of assets.	Decay of a substance over time
Asymptotic Behavior	The data approaches a limit but never quite reaches it, often observed in systems stabilizing at a certain level.	Temperature approaching room temperature but never exactly reaching it
Constant Doubling or Halving	The data consistently doubles or halves over fixed intervals, representing consistent growth or decay rates.	Population that doubles every year

Recognizing these patterns allows for easier interpretation of data trends and can inform strategic decisions, whether in business, science, or other fields. The ability to spot these patterns also aids in building mathematical models that accurately represent the observed behaviors in the data.

How to Verify Exponential Regression Answers

When working with mathematical models to represent data, it’s essential to verify the solutions you obtain. Ensuring that your calculations are correct and your predictions align with observed values is key to interpreting results accurately. This process involves checking both the model itself and its predictions to confirm they make sense given the original data.

Here are several steps to verify the validity of your model:

• Check the Residuals: After fitting a model, calculate the residuals–differences between the observed data points and the predicted values from the model. Ideally, these should be small and randomly distributed around zero, indicating that the model is a good fit for the data.
• Compare Predictions: Use the model to predict values for known data points. If the model’s predictions closely match the actual observed data, it suggests that the model is likely accurate.
• Plot the Model: Visualize the model alongside the original data on a graph. This can help identify whether the curve follows the general trend of the data, confirming its adequacy.
• Use Software Tools: Tools like graphing calculators or statistical software can provide detailed fit metrics, such as R-squared, which measures how well the model explains the data variability. A higher R-squared value indicates a better fit.

By following these steps, you can confidently assess whether your model appropriately represents the underlying data and refine your approach if needed. Verifying the solutions helps ensure that conclusions drawn from the model are reliable and meaningful in practical applications.

Advanced Strategies for Exponential Regression Questions

To excel in solving complex problems involving mathematical models, it is essential to apply advanced techniques that go beyond basic procedures. These strategies not only help in handling intricate calculations but also ensure that the solutions are more accurate and robust when dealing with real-world data. Mastering these techniques can significantly improve both your understanding and ability to solve problems efficiently.

Here are some advanced strategies to consider when tackling such problems:

• Transforming Data: In some cases, applying logarithmic transformations to the data can simplify the problem. By converting a multiplicative model into an additive one, you can apply linear regression techniques, making the problem easier to solve. This approach is especially useful when the data grows or decays exponentially.
• Using Software for Complex Fitting: For particularly challenging problems, utilizing software tools such as statistical calculators, Excel, or specialized programming languages like R or Python can help automate the fitting process. These tools allow for more precise calculations and can handle large datasets efficiently.
• Refining Model Selection: Not all models are created equal. When facing complex datasets, it is important to test multiple model types, not just the one that appears to fit initially. Consider testing variations and combinations of models to ensure that the one chosen best represents the data.
• Outlier Identification: Outliers can significantly affect the outcome of the model. Advanced strategies involve identifying and addressing outliers–either by removing them, adjusting them, or using robust methods that minimize their impact on the model’s accuracy.
• Cross-Validation: To ensure that the model is not overfitting, apply cross-validation techniques. This method involves splitting the dataset into multiple subsets, training the model on some of them, and testing it on the others. It helps confirm that the model generalizes well to new, unseen data.

By incorporating these advanced techniques, you can greatly enhance your ability to handle complex mathematical models and data analysis tasks. These strategies ensure not only better solutions but also a deeper understanding of the underlying principles, enabling more effective application in various fields.