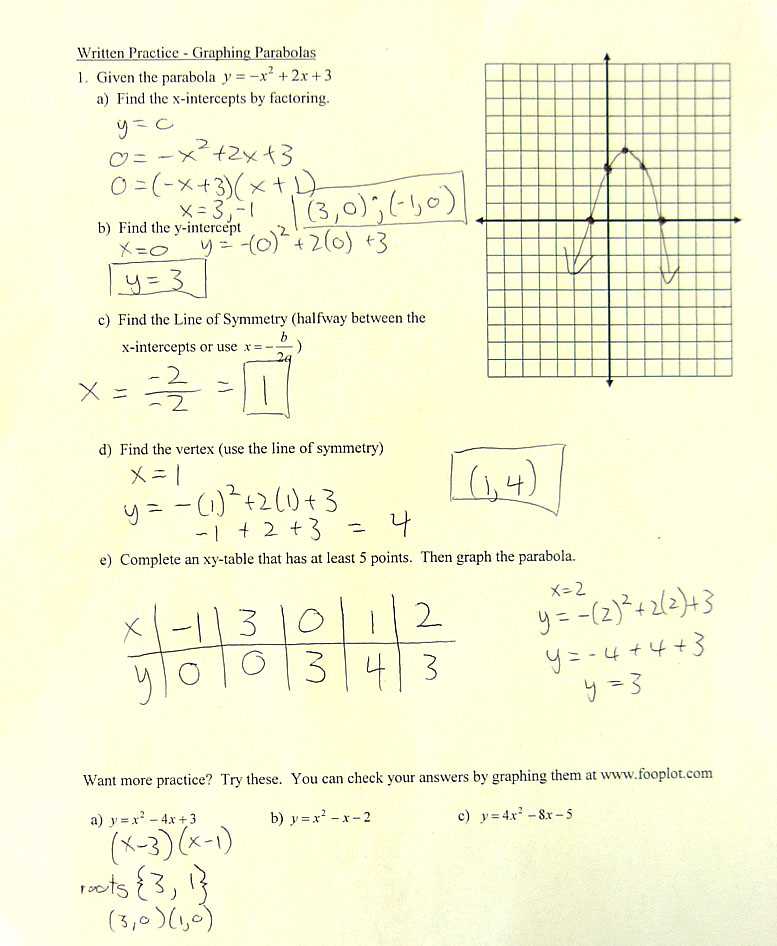
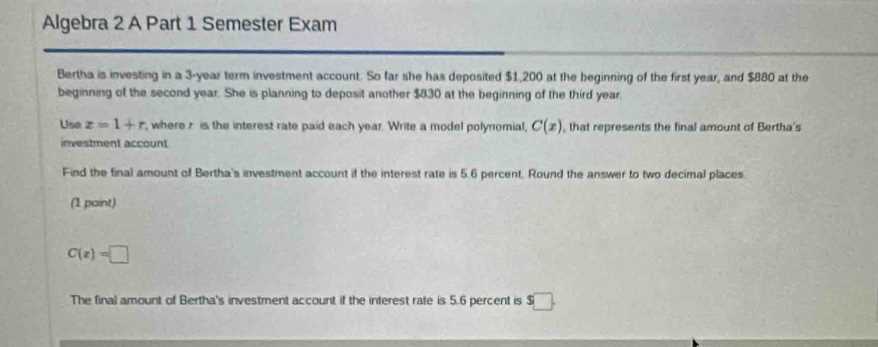
Algebra 2 Semester 2 Final Exam Answers Guide

algebra 2 semester 2 final exam answers

Preparing for an important academic evaluation can be both exciting and challenging. The material covered in your coursework often requires a deep understanding of core principles and problem-solving skills. Whether you’re revisiting fundamental concepts or tackling advanced topics, it’s essential to approach this stage with clarity and confidence.

In this guide, you’ll find valuable insights to help you navigate through complex problems. Focused practice and careful review can significantly improve your ability to handle various questions effectively. By mastering key topics and refining your strategies, you’ll enhance your performance and boost your confidence.

Every concept you’ve learned plays a crucial role in solving problems efficiently. Through systematic preparation, understanding patterns, and honing your technique, you’ll be better equipped to tackle even the most difficult challenges.

Algebra 2 Final Exam Preparation Tips

Effective preparation is the key to success when it comes to tackling a challenging academic assessment. A structured approach that combines focused review, practice, and strategy will help you perform at your best. By dedicating time to understanding core concepts and sharpening your problem-solving skills, you can face the test with confidence.

Focus on Key Topics

Identifying the most important areas of study will allow you to allocate your time wisely. Key concepts such as solving equations, working with functions, and understanding graphing techniques should be prioritized. Ensure you have a solid grasp on each topic by practicing problems and revisiting your notes regularly.

Practice Under Test Conditions

Simulating test conditions is one of the best ways to prepare for the real thing. Try solving problems within a set time limit to improve your speed and accuracy. This will help you manage time effectively and reduce anxiety during the actual assessment. Regular practice will also reinforce your understanding and boost your confidence.

Key Concepts for Semester 2 Exam

Understanding the core principles and building a strong foundation is crucial for success in any academic assessment. In this section, we will highlight the most essential topics you need to master. By focusing on these key concepts, you can streamline your preparation and boost your chances of performing well.

Here are the key areas to focus on:

Functions and Graphs: Understanding how different functions behave and how to graph them accurately is fundamental. Pay attention to linear, quadratic, and exponential functions.
Polynomials: Be sure to practice operations with polynomials, including addition, subtraction, multiplication, and factoring.
Rational Expressions: Master simplifying, multiplying, and dividing rational expressions and solving related equations.
Systems of Equations: Focus on solving linear and non-linear systems, both graphically and algebraically.
Exponents and Radicals: Work on simplifying expressions with exponents and radicals, including solving equations that involve them.
Sequences and Series: Understand arithmetic and geometric sequences, and how to find their sums.
Trigonometry: While often introduced earlier, trigonometric functions and their applications remain important. Be prepared to solve problems involving angles and ratios.

By concentrating on these areas, you will have a solid understanding of the material and be ready to tackle the test effectively.

How to Solve Quadratic Equations

Solving quadratic equations is an essential skill that requires understanding different methods to find the roots of the equation. Quadratic expressions are typically written in the form of ax² + bx + c = 0, and the goal is to determine the values of the variable that satisfy the equation. By mastering the various techniques available, you can confidently approach and solve these types of problems.

Using the Quadratic Formula

The quadratic formula is a reliable method to solve any quadratic equation, regardless of whether the equation can be factored easily. The formula is:

x = (-b ± √(b² – 4ac)) / 2a

Simply plug the values of a, b, and c from your equation into the formula, and calculate the discriminant (b² – 4ac). Depending on the value of the discriminant, you will have either two real roots, one real root, or no real solutions.

Factoring the Equation

When possible, factoring is a quicker and simpler method to solve quadratic equations. To use factoring, first rewrite the equation in standard form (ax² + bx + c = 0). Then, find two numbers that multiply to give ac (the product of a and c) and add up to b. Once you identify these numbers, split the middle term and factor the expression into two binomials. Solve for the variable by setting each factor equal to zero.

Factoring works best when the equation can be factored easily, so always look for common factors first before attempting more complex methods.

Understanding Functions and Their Graphs

Functions and their corresponding graphs are foundational concepts in mathematics that help describe relationships between variables. The graph of a function visually represents how one quantity changes in relation to another, and understanding these graphs is key to solving problems and interpreting real-world scenarios. In this section, we’ll explore the essential aspects of functions and how to interpret their graphs effectively.

To get a clear understanding, focus on the following key elements of functions:

Domain and Range: The domain refers to all possible input values, while the range refers to all possible output values of a function. Knowing both helps in graphing and analyzing the function’s behavior.
Intercepts: The points where the graph crosses the x-axis (x-intercepts) and the y-axis (y-intercepts) are important for understanding the function’s behavior and finding solutions.
Asymptotes: Some functions have lines they approach but never touch. These lines, called asymptotes, provide insight into the long-term behavior of the function.
Increasing and Decreasing Intervals: Identifying where the function is increasing or decreasing helps in understanding how it behaves over different regions.
End Behavior: Understanding what happens to the function’s values as the input gets very large or very small helps predict the function’s behavior at extremes.

To graph a function, start by plotting key points and identifying the overall shape based on the function type. Common types of graphs include linear, quadratic, cubic, and exponential, each having unique characteristics.

By practicing with different functions and their graphs, you’ll develop the ability to quickly interpret and solve related problems.

Mastering Polynomials for the Test

algebra 2 semester 2 final exam answers

Polynomials are a fundamental aspect of many mathematical problems, and mastering their manipulation is crucial for performing well in any assessment. Whether it’s simplifying expressions, performing operations, or solving polynomial equations, understanding the key techniques will ensure you can tackle these problems with confidence. The ability to handle polynomials with ease is essential for success in various types of questions.

Here are the essential polynomial operations and strategies to focus on:

Operation	Description	Example
Addition/Subtraction	Combine like terms by adding or subtracting coefficients of terms with the same degree.	(3x² + 5x) + (2x² – 4x) = 5x² + x
Multiplication	Multiply each term in one polynomial by every term in the other polynomial.	(x + 2)(x – 3) = x² – x – 6
Factoring	Factor polynomials by finding common factors or using methods like grouping or the quadratic method.	x² + 5x + 6 = (x + 2)(x + 3)
Division	Divide one polynomial by another using long division or synthetic division.	Divide x³ – 2x² + 4x by x – 1 using synthetic division.

By mastering these key techniques, you’ll be able to tackle polynomial-related questions more efficiently and accurately. Practice regularly to ensure you’re familiar with the methods and ready to apply them on test day.

Solving Rational Expressions Efficiently

Working with rational expressions requires a solid understanding of how to simplify and manipulate fractions involving polynomials. Whether you’re adding, subtracting, multiplying, or dividing these expressions, the key is to approach each problem systematically. By mastering efficient techniques for handling rational expressions, you’ll save time and ensure accuracy in solving complex problems.

Here are some steps to solve rational expressions more effectively:

Simplify before solving: Always look for common factors in the numerator and denominator. Factor both expressions as much as possible before performing any operations. This can often lead to simpler expressions and prevent unnecessary complications.
Find a common denominator: When adding or subtracting rational expressions, it’s crucial to find a common denominator. This allows you to combine terms efficiently and avoid errors.
Cancel common factors: After factoring the numerator and denominator, check for any common terms that can be canceled out. This step can significantly simplify your calculations and make the process quicker.
Multiply and divide directly: For multiplication and division, always multiply numerators together and denominators together. Don’t forget to simplify before completing the final answer.

By following these strategies, you can solve rational expressions quickly and accurately. Consistent practice with these techniques will improve your overall problem-solving efficiency and help you perform better on any related tasks.

Practice with Exponential Functions

Exponential functions describe many real-world phenomena, such as population growth, radioactive decay, and financial investments. Understanding how to work with these functions is essential for solving problems that involve rapid change. By practicing different aspects of exponential functions, you can become more comfortable with manipulating and analyzing them in various contexts.

Key Properties of Exponential Functions

Before solving problems, it’s important to understand the basic properties of exponential functions. The general form of an exponential function is:

f(x) = a * b^x

Where “a” is the initial value, “b” is the base, and “x” is the exponent. The key properties to focus on are:

Growth vs. Decay: When the base “b” is greater than 1, the function represents exponential growth. If the base is between 0 and 1, it represents exponential decay.
Horizontal Asymptote: Exponential functions have a horizontal asymptote at y = 0, meaning the function approaches but never touches the x-axis.
Rate of Change: The rate of change in an exponential function is proportional to the current value, which results in rapid growth or decay over time.

Example Problems

To practice working with exponential functions, consider these example problems:

Problem	Solution
Solve for x: 5 * 2^x = 40	First, divide both sides by 5: 2^x = 8. Since 8 = 2^3, we can conclude that x = 3.
Find the value of f(x) for x = 4: f(x) = 3 * (1/2)^x	Substitute x = 4 into the function: f(4) = 3 * (1/2)^4 = 3 * 1/16 = 3/16.
Graph the function f(x) = 2 * 3^x	The graph will show exponential growth, with a horizontal asymptote at y = 0. As x increases, the value of f(x) will grow rapidly.

By practicing with exponential functions and understanding their properties, you can gain confidence in solving more complex problems and analyzing their real-world applications.

Tips for Logarithmic Problem Solving

Logarithmic functions often seem tricky at first, but with the right approach, solving problems involving them can become much more manageable. The key is to understand the underlying concepts and recognize when to apply specific rules. By mastering a few essential techniques, you can tackle logarithmic problems with confidence and efficiency.

Understanding Key Logarithmic Properties

Logarithmic functions are the inverse of exponential functions, and knowing how to manipulate these expressions is crucial. Here are some fundamental properties to keep in mind:

Logarithmic Identity: log_b(b) = 1. This is because the logarithm of a number to its own base is always 1.
Product Rule: log_b(xy) = log_b(x) + log_b(y). This rule allows you to split a logarithmic expression into simpler parts.
Quotient Rule: log_b(x/y) = log_b(x) – log_b(y). Use this when dealing with division inside the logarithm.
Power Rule: log_b(x^n) = n * log_b(x). This is helpful when the argument of the logarithm is raised to a power.

Step-by-Step Approach to Solving Logarithmic Problems

When faced with a logarithmic problem, follow these steps to solve it efficiently:

Rewrite the problem: If possible, rewrite the logarithmic expression in exponential form. This often simplifies the problem and makes it easier to solve.
Use logarithmic properties: Apply the product, quotient, and power rules to break down complex expressions into simpler components.
Solve for the unknown: Once you have simplified the expression, solve for the unknown variable, just as you would with an algebraic equation.
Check your work: Always verify that your solution makes sense by plugging it back into the original equation to ensure consistency.

By practicing these strategies, you’ll improve your ability to solve logarithmic problems and gain a deeper understanding of their applications in various mathematical contexts.

Mastering Systems of Equations

Solving systems of equations involves finding values for variables that satisfy multiple equations simultaneously. These problems can arise in various contexts, from determining the intersection of lines to solving real-world problems involving multiple conditions. By mastering the methods for solving these systems, you can approach these challenges with greater ease and precision.

There are several techniques used to solve systems of equations, each suitable for different types of problems. The most common methods include substitution, elimination, and graphing. Understanding when to apply each method is key to solving these problems efficiently.

To solve a system, the goal is to manipulate the equations so that the unknowns can be isolated and solved. Whether you’re working with two variables or more complex systems, breaking down the problem into manageable steps will lead to a more effective solution.

With consistent practice, solving systems of equations becomes a straightforward process, and you’ll develop a deeper understanding of how different variables relate to one another within various constraints. Mastering these techniques will improve your ability to approach a wide range of mathematical problems with confidence and accuracy.

Reviewing Sequences and Series Concepts

Sequences and series are fundamental topics that involve ordered lists of numbers and their summation, respectively. Understanding the behavior of these patterns is essential for solving problems related to progression and accumulation. Whether you are dealing with arithmetic, geometric, or more complex patterns, grasping these concepts will provide you with the tools needed to analyze and solve a variety of mathematical problems.

Arithmetic and Geometric Sequences

Two of the most commonly studied types of sequences are arithmetic and geometric sequences. In an arithmetic sequence, the difference between consecutive terms is constant, while in a geometric sequence, the ratio between consecutive terms is constant. Understanding the general formulas for these sequences is crucial for solving problems.

Sequence Type	General Formula
Arithmetic Sequence	a_n = a₁ + (n – 1) * d
Geometric Sequence	a_n = a₁ * r^{n – 1}

Understanding Series

A series is the sum of the terms of a sequence. For arithmetic and geometric sequences, there are specific formulas to calculate the sum of the first n terms. Recognizing when to use these formulas can significantly simplify the process of solving problems involving sums of sequences.

Series Type	Sum Formula
Arithmetic Series	S_n = (n/2) * (2a₁ + (n – 1) * d)
Geometric Series	S_n = a₁ * ((1 – rⁿ) / (1 – r))

By reviewing these key concepts and formulas, you can effectively solve problems related to both sequences and series, helping to strengthen your overall problem-solving skills.

Essential Trigonometry for Algebra 2

Understanding the basic principles of trigonometry is crucial for solving problems involving angles, waves, and periodic functions. This branch of mathematics provides essential tools for analyzing geometric shapes and their properties, particularly when working with right triangles or circular motion. Mastering these concepts helps students better understand relationships between sides and angles in various contexts.

Key Trigonometric Functions

Trigonometry revolves around three primary functions: sine, cosine, and tangent. These functions relate the angles of a right triangle to the ratios of its sides. By learning these relationships, you can find unknown angles or side lengths in various geometric problems.

Sine (sin): The ratio of the opposite side to the hypotenuse.
Cosine (cos): The ratio of the adjacent side to the hypotenuse.
Tangent (tan): The ratio of the opposite side to the adjacent side.

Using Trigonometric Identities

Trigonometric identities are equations that express relationships between the different trigonometric functions. These identities are useful for simplifying expressions, solving equations, and verifying equations. Familiarity with the most commonly used identities will allow you to approach problems more efficiently.

Pythagorean Identity: sin²θ + cos²θ = 1
Angle Sum and Difference Identities: These help you solve for unknown angles using known values.

By mastering these fundamental trigonometric principles, you’ll be able to approach more advanced problems with confidence and improve your overall problem-solving skills in mathematics.

Using Matrices in Algebra 2 Exams

Matrices are powerful tools used to organize and manipulate numerical data, especially in solving systems of linear equations and performing transformations. Their application is essential in various mathematical problems, where they provide an efficient method to handle multiple variables and complex relationships. Mastering matrices allows students to streamline calculations and solve problems involving large sets of equations quickly.

Matrix Operations

algebra 2 semester 2 final exam answers

Understanding how to perform basic operations on matrices is key to solving problems. These operations include addition, subtraction, multiplication, and finding the determinant or inverse of a matrix. Each operation serves a specific purpose and is useful for solving different types of problems, such as solving systems of linear equations or working with transformations in geometry.

Matrix Addition: Adding corresponding elements from two matrices of the same dimensions.
Matrix Multiplication: The product of two matrices, where the number of columns in the first matrix equals the number of rows in the second matrix.
Inverse Matrix: Used to solve matrix equations, particularly for systems of equations.

Applications in Solving Systems

Matrices are particularly useful for solving systems of linear equations, where traditional methods like substitution and elimination can become cumbersome. By converting a system of equations into a matrix, you can apply row operations to simplify and solve for the variables. This method is not only efficient but also highly effective when dealing with larger systems.

Row Reduction: A method to simplify a matrix into row echelon form, making it easier to solve for unknowns.
Determinants: The determinant helps determine whether a system of equations has a unique solution or not.

By mastering matrix operations and their applications, you will be able to approach problems involving multiple variables more confidently, ensuring a more efficient and accurate problem-solving process.

How to Tackle Word Problems

Word problems often require careful reading and logical thinking to translate real-world scenarios into mathematical equations. The key to solving these problems lies in breaking down the information, identifying the unknowns, and applying the appropriate mathematical techniques. By following a step-by-step approach, you can simplify complex situations and find the solution efficiently.

Step 1: Understand the Problem

The first step is to thoroughly read the problem and make sure you understand the scenario. Look for key information, such as quantities, relationships, and what needs to be solved. It’s important to highlight or underline important details that will help you form the necessary equations.

Step 2: Define Variables

Once you’ve identified the relevant information, define variables to represent the unknowns. This allows you to set up an equation based on the situation. For example, if the problem involves a total cost and you need to find the price of individual items, assign a variable to represent the price of one item.

Step 3: Set Up Equations

Using the information gathered, translate the word problem into one or more mathematical equations. Pay attention to keywords like “sum,” “difference,” “product,” or “quotient,” which indicate the type of operation needed. For example, if two quantities are added together to give a total, use the addition operation to express the relationship.

Step 4: Solve the Equations

After setting up the equation(s), solve for the unknowns using the appropriate methods. This could involve solving linear equations, systems of equations, or applying specific formulas based on the problem’s context.

Step 5: Verify the Solution

Once you find the solution, it’s important to check your work by plugging the values back into the original problem. Ensure that the solution makes sense in the context of the problem and that all the given conditions are satisfied.

By practicing these steps regularly, you will become more adept at tackling word problems and applying mathematical concepts to real-world situations.

Graphing Inequalities for Success

Graphing inequalities is a crucial skill that allows you to visually represent the solution sets of various mathematical situations. Understanding how to correctly plot these inequalities on a coordinate plane is essential for solving real-world problems and making connections between abstract concepts. By following a systematic approach, you can successfully graph inequalities and understand their implications.

Steps to Graph Inequalities

To graph inequalities effectively, follow these key steps:

Rewrite the inequality in slope-intercept form if necessary. This makes it easier to graph the boundary line or curve, especially for linear inequalities.
Plot the boundary line or curve. For linear inequalities, draw the corresponding line (solid for ≤ or ≥, dashed for ). For non-linear inequalities, graph the corresponding curve.
Choose a test point (usually (0, 0) unless it’s on the boundary) to determine which side of the line or curve represents the solution set. If the test point satisfies the inequality, shade the region containing that point.
Shade the correct region based on the test point. This shaded area represents all the solutions to the inequality.

Tips for Success

Mastering the graphing of inequalities requires practice and attention to detail. Here are some additional tips:

Use clear labeling for the axes, boundary lines, and shaded regions to avoid confusion.
Check your work by testing a point from the shaded region to confirm that it satisfies the inequality.
Practice different types of inequalities, including those involving absolute values or quadratic functions, to become comfortable with a wide range of scenarios.

By following these guidelines and practicing regularly, you’ll be able to graph inequalities accurately and with confidence, setting yourself up for success in future problem-solving challenges.

Common Mistakes to Avoid in Algebra 2

In the study of advanced mathematical concepts, making small errors can lead to bigger problems. Understanding the common pitfalls and how to avoid them is crucial to mastering the subject. By being aware of these typical mistakes, you can streamline your learning and improve your accuracy in problem-solving.

Common Errors to Watch Out For

Here are some frequent mistakes to avoid:

Incorrectly solving equations: When simplifying expressions, it’s easy to forget to apply the correct order of operations, leading to incorrect solutions.
Misinterpreting signs: Pay close attention to positive and negative signs. A small mistake in sign can drastically alter the result of your calculation.
Overlooking restrictions: Some problems involve constraints, such as restrictions on domain or range. Forgetting to account for these can result in invalid solutions.
Skipping steps in complex calculations: Rushing through multi-step problems can lead to missing crucial parts of the solution. Always follow a methodical process.
Confusing similar concepts: Many mathematical principles appear similar, such as linear and quadratic functions. Make sure to distinguish between them to avoid errors in application.

Tips for Avoiding Mistakes

To prevent these common errors, here are a few tips:

Take your time: Rushing through problems is a surefire way to make mistakes. Focus on accuracy rather than speed.
Double-check your work: Always review your calculations to ensure no small mistakes have been overlooked.
Practice regularly: The more you practice, the more familiar you become with the processes, helping to reduce errors.
Ask for help when needed: If you’re unsure about a concept or step, don’t hesitate to seek clarification from a teacher or peer.

By being mindful of these common errors and implementing these strategies, you can avoid mistakes and improve your problem-solving skills.

Test-Taking Strategies for Algebra 2

Success in a mathematics assessment often hinges not only on your understanding of the concepts but also on how you approach the test itself. Effective test-taking strategies can help you manage time efficiently, reduce stress, and maximize your performance. By incorporating certain tactics, you can boost your confidence and enhance your chances of achieving the best possible results.

Key Strategies for Success

Implementing these strategies during your test can lead to more effective problem-solving:

Read questions carefully: It’s easy to overlook small details when under time pressure. Make sure you fully understand each question before starting your calculations.
Start with familiar problems: Begin with the questions you feel most confident about. This helps build momentum and ensures you’re not wasting time on questions that seem more difficult.
Manage your time wisely: Allocate a set amount of time for each section or problem, ensuring you have time to address all questions. Don’t spend too long on any one problem.
Show your work: Even if you’re confident in your answer, writing out your steps can help you avoid mistakes and may earn partial credit in case of errors.
Review your answers: If time allows, double-check your calculations and ensure all answers make sense. A quick review can help you catch any careless mistakes.

Dealing with Stress and Anxiety

Maintaining a calm mindset is crucial for optimal performance. Consider the following tips to manage stress during the test:

Stay organized: Keep your workspace neat and your notes well-organized. This reduces distractions and helps you find information quickly when needed.
Take deep breaths: If you begin to feel overwhelmed, pause for a moment, take a few deep breaths, and refocus.
Don’t rush: Focus on accuracy rather than speed. If you make an error, correct it carefully rather than panicking.

By combining these strategies, you can enhance your test-taking skills, reduce anxiety, and improve your performance in any mathematical assessment.

Final Review Checklist for Algebra 2 Exam

Preparing for a major assessment requires careful planning and a focused review. Having a checklist ensures that no essential topics are overlooked, and that you’re fully prepared for all types of problems you may encounter. Below is a structured list to help you methodically go over key concepts and ensure you’re ready for the test.

Understand Key Concepts: Make sure you grasp the main principles behind all the major topics, such as equations, functions, and graphing methods.
Practice Problem-Solving: Solve problems from various sections to test your understanding. Focus on areas that have been challenging for you during the course.
Review Core Formulas: Go over all the critical formulas and their applications. Be sure you can recall them quickly during the assessment.
Check for Common Mistakes: Identify areas where you tend to make errors and practice those problems. This helps build confidence and accuracy.
Understand Word Problems: Work through word problems to ensure you’re comfortable translating real-world scenarios into mathematical expressions.
Graphing Techniques: Be sure you’re able to quickly and accurately plot graphs and interpret them correctly, particularly for more complex functions.
Test Timing: Practice solving problems within a time limit to get comfortable with the pacing of the test. Aim to finish each section in a reasonable time frame.

As you review, take note of any areas where you feel less confident and spend extra time reinforcing your understanding. The more thorough your review, the more prepared you’ll feel on test day.

Resources for Additional Algebra Practice

Supplementing your study with additional resources can greatly improve your understanding and boost your confidence. Whether you’re looking to reinforce concepts or challenge yourself with more complex problems, there are plenty of tools available to help you practice. Here are some great options for expanding your knowledge and mastering key concepts.

Online Learning Platforms

Khan Academy: This free resource offers comprehensive lessons and practice exercises on a wide range of topics, from basic concepts to advanced techniques. Videos and interactive problems provide a hands-on way to learn.
Coursera: For a more structured learning experience, Coursera offers courses from top universities. These courses often include practice tests and assignments that can help you master the material.
Desmos: Known for its graphing calculator, Desmos also offers a variety of interactive lessons to help you visualize equations and functions. It’s an excellent tool for understanding graphs and their properties.

Practice Problem Websites

IXL: IXL provides practice problems across many subjects, allowing you to work at your own pace. It adapts to your skill level, offering problems that challenge you as you improve.
Paul’s Online Math Notes: This site offers practice problems, notes, and explanations on a wide range of math topics. It’s especially helpful for reviewing step-by-step solutions.
Brilliant.org: Brilliant offers interactive problems and puzzles that allow you to think critically and explore mathematical concepts in a deep, engaging way.

Using these resources, you can reinforce your knowledge and sharpen your problem-solving skills. Consistent practice is key to mastering challenging material and ensuring you’re prepared for any type of problem-solving scenario.