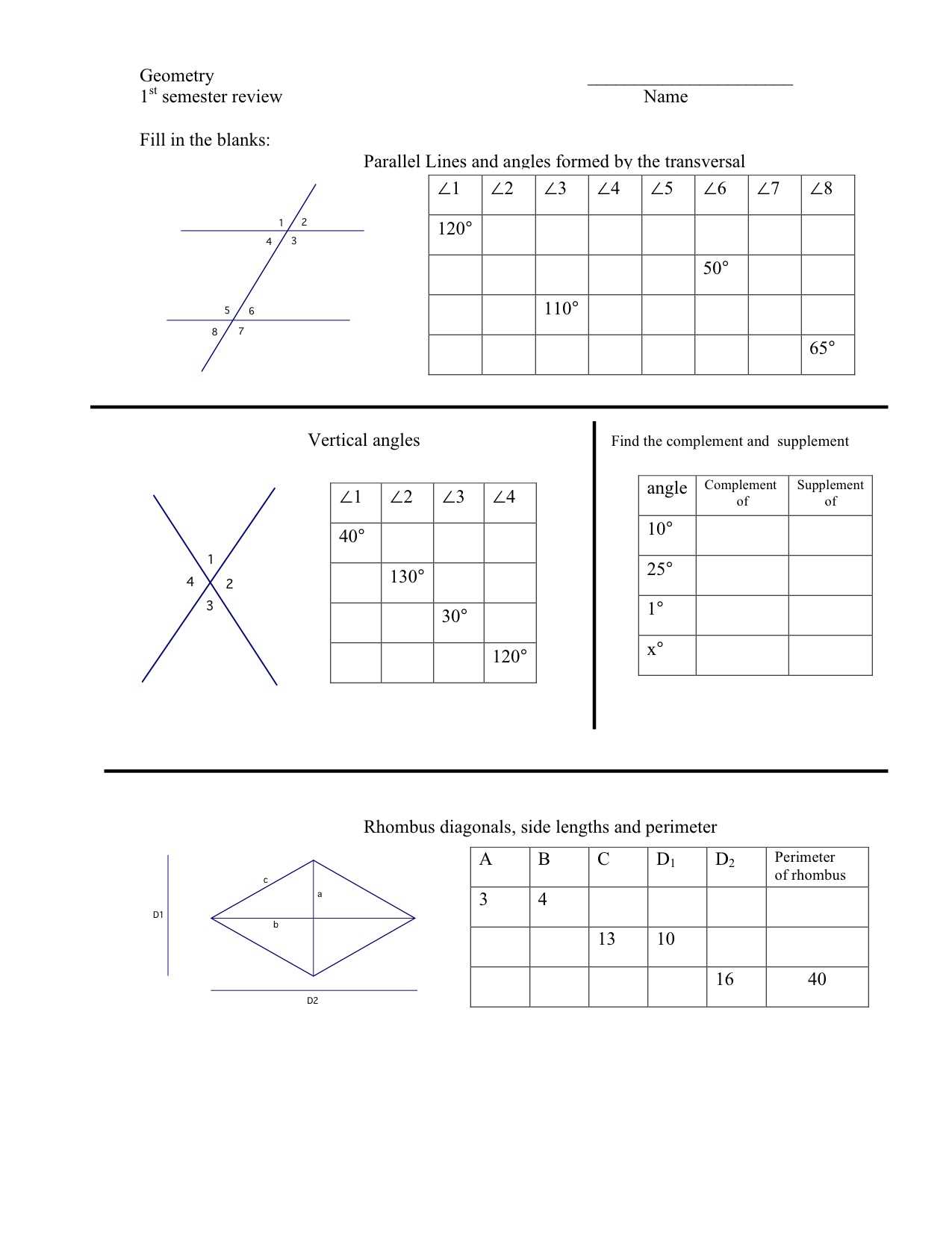
Geometry First Semester Exam Answers

Preparing for a challenging test in mathematical reasoning involves understanding core principles, sharpening problem-solving skills, and applying knowledge effectively. Success comes from a solid grasp of concepts and the ability to approach each task methodically.

With the right approach, tackling complex questions becomes a more manageable process. The key is practice and familiarity with different types of problems that are typically presented. Developing a strategy for time management and error-checking will also help maximize performance.

Preparation is crucial to ensure confidence when faced with difficult questions. Taking the time to review common patterns and techniques, along with applying learned methods, can make a significant difference in outcomes.

Mastery comes with repetition and understanding the underlying structures, leading to more efficient problem-solving and better results under pressure.

Geometry First Semester Exam Answers

When preparing for a test in mathematical reasoning, it is important to understand the underlying principles and methods needed to solve various types of problems. By focusing on key strategies and practice techniques, students can enhance their problem-solving skills and achieve success when faced with complex tasks.

Reviewing essential concepts, such as shapes, angles, and measurement principles, will allow individuals to tackle questions with confidence. Understanding the relationships between different elements and practicing the application of formulas plays a critical role in mastering the material.

In addition to conceptual knowledge, effective time management and error-checking techniques are crucial for achieving the best possible results. Developing a systematic approach to solving problems will help minimize mistakes and maximize efficiency during the test.

Key Concepts to Understand for the Exam

To excel in the assessment, it’s essential to have a strong grasp of fundamental principles. Mastering core ideas allows for a clearer understanding of complex problems and streamlines the approach to solving them.

The following topics are crucial to understand before the test:

• Understanding shapes and their properties
• Familiarity with angles, their types, and how to measure them
• Mastering formulas for calculating areas, volumes, and perimeters
• Recognizing different types of transformations, including rotations and reflections
• Grasping the concept of symmetry and its applications in problem-solving

By focusing on these key areas, you’ll build a strong foundation for tackling even the most difficult questions. Regular practice and application of these concepts will reinforce your understanding and improve your performance.

How to Approach Geometry Problems Effectively

Approaching mathematical problems with a systematic and focused strategy is key to solving them accurately and efficiently. By breaking down complex tasks into manageable steps, you can avoid confusion and reduce the likelihood of errors. Understanding the best methods for tackling each type of problem will help you work through challenges with confidence.

Start with a Clear Understanding

Before diving into calculations or applying formulas, take a moment to carefully read the problem. Identify all given information and highlight key elements such as dimensions, angles, and relationships between objects. This will give you a solid foundation on which to build your solution.

Apply Logical Steps and Check Your Work

Once you have a clear understanding, approach the problem using logical steps. Begin with the simplest relationships and gradually move toward more complex solutions. As you work through the problem, continuously check your progress to ensure accuracy. If possible, revisit earlier steps to confirm that no mistakes were made along the way.

Practice and consistency are essential for honing problem-solving skills. The more you familiarize yourself with different problem types, the easier it becomes to apply the right strategies in various situations.

Common Mistakes to Avoid During the Test

Even the most prepared individuals can make simple errors when under pressure. Recognizing and avoiding common pitfalls is crucial to ensuring you perform at your best during the assessment. Many mistakes can be easily prevented with careful attention and a methodical approach.

Misinterpreting the Problem

One of the most frequent mistakes is misreading the question or overlooking important details. Be sure to carefully analyze the information provided and double-check the specific requirements. Taking the time to fully understand the problem will prevent unnecessary errors.

Skipping Steps or Rushing

In the rush to finish, many individuals skip intermediate steps or make assumptions without justification. Always work through the process step by step, even if you think you know the answer. This ensures that your reasoning is sound and helps avoid mistakes due to overlooked details.

Careful review of your work is essential to catch errors before submitting your answers. By managing your time effectively and maintaining focus, you can minimize the risk of mistakes and improve your overall performance.

Step-by-Step Guide to Solving Geometry Questions

To effectively solve complex problems in mathematical reasoning, it’s important to follow a structured approach. By breaking down each task into smaller, manageable steps, you can ensure that no detail is overlooked and that you remain focused throughout the process. This method will help you tackle questions more confidently and accurately.

1. Understand the Problem

The first step is to carefully read and understand the question. Identify all the given information and determine what is being asked. Pay attention to keywords and important details that will guide your solution.

• Highlight the key values and relationships in the problem.
• Make note of any required calculations or steps mentioned in the question.

2. Organize Your Approach

Once you understand the problem, plan how you will approach it. This involves choosing the right method and applying the correct formulas or principles. Consider drawing diagrams to visually represent the situation.

• Identify any relevant formulas or rules that apply.
• If applicable, sketch a diagram or visual representation of the problem.

3. Solve the Problem

Now that you have a plan in place, begin solving the problem step by step. Work methodically and make sure each step is logical and follows from the previous one. Avoid jumping ahead to the solution without verifying each part of the process.

4. Check Your Work

Before finalizing your answer, review your steps and calculations. Ensure that you haven’t missed anything and that your solution is both complete and accurate. If possible, verify your answer using an alternative method.

By following these steps, you can systematically work through problems, reducing the likelihood of mistakes and increasing your chances of success.

Understanding Geometry Proofs and Theorems

Mastering logical reasoning is essential for solving complex problems that require more than just applying formulas. Proofs and theorems form the foundation of many mathematical tasks, allowing you to validate relationships between different elements. Developing a clear understanding of these concepts enables you to approach challenges with a structured mindset and ensures that solutions are both accurate and reliable.

The Role of Proofs in Mathematics

Proofs are step-by-step logical arguments used to demonstrate the validity of a particular statement. Each statement in a proof is supported by previously established facts or axioms. The ability to construct a solid proof requires a deep understanding of the relationships between objects and their properties.

• Identify the given information clearly.
• Determine the conclusion or statement to be proven.
• Use known rules, postulates, and properties to build the logical chain of reasoning.

Applying Theorems Effectively

Theorems are established statements that have been proven true based on logical arguments. To apply a theorem correctly, it’s important to understand both its assumptions and its conclusions. Recognizing when and how to use theorems can simplify complex problems significantly.

• Review and memorize key theorems that apply to common problem types.
• Carefully consider the conditions under which each theorem is valid.

By improving your understanding of proofs and theorems, you enhance your ability to solve problems not just by applying formulas, but by understanding the deeper principles that govern mathematical relationships.

Tips for Memorizing Geometric Formulas

Memorizing formulas is crucial for solving problems efficiently, especially when time is limited. Rather than trying to memorize everything at once, focusing on understanding the underlying concepts and then committing key formulas to memory will make the process easier. Utilizing various techniques can improve retention and recall when needed.

1. Break Formulas into Smaller Parts

Rather than memorizing a long and complex formula in its entirety, break it down into smaller, more manageable components. By understanding each part, you’ll be able to recall it more easily and apply it correctly when solving problems.

• Divide formulas into variables and constants.
• Identify patterns and relationships within each formula.

2. Use Mnemonics and Visual Aids

Creating mnemonic devices or visual aids can help solidify formulas in your memory. A catchy phrase or a diagram can serve as a useful reminder when you’re in the middle of solving a problem.

• Create memorable acronyms or phrases to represent formulas.
• Use drawings or diagrams to visualize the relationships between elements.

3. Practice and Repetition

Consistent practice and repetition are essential for reinforcing what you’ve learned. Regularly solving problems that involve different formulas will help you recall them faster and apply them correctly under pressure.

• Work through practice problems daily.
• Test yourself regularly to reinforce your memory.

4. Group Formulas by Type

Organizing formulas into groups based on their function or category will make it easier to remember. For example, grouping formulas related to areas, volumes, and surface areas together helps you recall them faster when needed.

• Group formulas for shapes, transformations, and measurements.
• Review one group of formulas at a time to avoid confusion.

By applying these techniques, you can make memorization more effective and feel more confident when applying formulas during problem-solving.

Practice Questions for Geometry Success

Reinforcing your knowledge with regular practice is one of the best ways to ensure success. Practicing problems of varying difficulty helps you become familiar with different scenarios and improve problem-solving techniques. The more you practice, the more confident and efficient you become in applying concepts.

Basic Questions

Start with simple problems to build a strong foundation. These questions will help you get comfortable with the core concepts and basic calculations.

Question	Answer
Calculate the perimeter of a rectangle with length 5 cm and width 3 cm.	Perimeter = 2(5 + 3) = 16 cm
What is the area of a circle with a radius of 4 cm?	Area = π * 4² = 50.27 cm²

Intermediate Questions

Once you feel comfortable with basic problems, move on to intermediate questions that require a deeper understanding of formulas and relationships between elements.

Question	Answer
Find the volume of a cylinder with radius 3 cm and height 7 cm.	Volume = π * 3² * 7 = 197.92 cm³
Determine the length of the hypotenuse in a right triangle with legs of 6 cm and 8 cm.	Hypotenuse = √(6² + 8²) = 10 cm

By regularly practicing a range of problems, you will reinforce key concepts and increase your ability to solve more challenging questions with ease.

Time Management Strategies for Geometry Exams

Effective time management is key to success during any timed assessment. Properly allocating time for each question can help ensure that you complete all sections and avoid rushing through complex problems. By practicing strategic planning and prioritization, you can maximize your performance and reduce stress during the test.

1. Prioritize Easy Questions

Start by tackling the questions you find easiest. This allows you to build momentum and gain confidence early on. By completing simpler problems quickly, you’ll free up more time for the more challenging ones.

• Skim through the test and identify questions you can solve quickly.
• Do not dwell too long on questions you find difficult; come back to them later.

2. Allocate Time to Each Section

Before you begin, divide the total time available by the number of sections or questions. This will give you a clear sense of how much time to spend on each part, helping you stay on track. Ensure you leave a few minutes at the end to review your work.

• Use a watch or timer to keep track of time spent on each question.
• Be mindful of the total time remaining and adjust as needed.

By applying these time management strategies, you can approach the test with a calm and focused mindset, ensuring that you make the best use of your time and complete the assessment to the best of your ability.

Geometry Exam Review Techniques

Effective review techniques are essential for solidifying knowledge and boosting confidence before a test. Focusing on understanding key concepts and practicing problem-solving strategies is crucial. By adopting a systematic approach, you can maximize your retention and ensure you are well-prepared for any question that might arise during the assessment.

1. Focus on Core Concepts

Identify the most important concepts that are likely to be tested. This includes reviewing key formulas, theorems, and relationships between different elements. Rather than memorizing information blindly, try to understand the logic behind each concept, as this will help you solve problems more effectively during the test.

2. Practice Past Problems

Revisiting past problems is one of the most efficient ways to prepare. These problems can give you insight into the format of the test and the types of questions that are typically asked. By solving a variety of problems, you’ll build familiarity with different problem types and improve your ability to solve them under time constraints.

3. Use Active Recall and Spaced Repetition

Instead of passively reviewing notes or textbooks, actively quiz yourself on key topics. Spaced repetition, which involves reviewing material at increasing intervals, has been shown to improve long-term retention. This method ensures that you’re constantly reinforcing your knowledge without overwhelming yourself.

4. Collaborate with Study Groups

Studying in groups can be beneficial, as it allows you to discuss and explain concepts with others. This collaborative approach can help clarify any misunderstandings and reinforce your knowledge through teaching. However, make sure to stay focused and avoid distractions during study sessions.

5. Simulate Test Conditions

Taking practice tests under timed conditions helps simulate the real test environment. This not only familiarizes you with the types of questions but also helps you manage your time effectively. By replicating the pressure of an actual test, you’ll build your confidence and identify areas where you need to improve.

By incorporating these review techniques into your study routine, you’ll be well-equipped to tackle the test with a clear understanding of the material and the ability to solve problems efficiently. Regular practice and focused review are key to success.

Essential Geometry Terms to Remember

Mastering key terms is crucial for understanding the concepts that form the foundation of the subject. These terms are essential for both solving problems and grasping the relationships between different shapes, angles, and measurements. A solid grasp of these terms will help you navigate through various problems with ease and accuracy.

1. Point

A fundamental concept that represents a location in space, without any length, width, or depth. It is typically used to mark positions and is often labeled with a capital letter.

2. Line

A one-dimensional figure that extends infinitely in both directions. It is defined by two points and has no curvature.

3. Angle

The space between two intersecting lines or rays, measured in degrees. Angles are classified based on their size, such as acute, right, and obtuse.

4. Triangle

A polygon with three sides and three angles. The types of triangles are determined by their angles (e.g., equilateral, isosceles, scalene) and side lengths.

5. Circle

A round shape defined by all points that are a fixed distance (radius) from a central point (center).

6. Perimeter

The total length of the boundary of a two-dimensional shape, calculated by adding the lengths of its sides.

7. Area

The measure of the surface of a shape. It is expressed in square units and is calculated differently for various shapes (e.g., length × width for rectangles, πr² for circles).

8. Volume

The amount of space occupied by a three-dimensional object. Volume is typically measured in cubic units.

9. Parallel Lines

Two lines that never intersect, no matter how far they are extended. They have the same slope and are always equidistant from each other.

10. Perpendicular Lines

Lines that intersect at a right angle (90 degrees). They are crucial for creating right triangles and understanding certain properties in shapes.

11. Radius

The distance from the center of a circle to any point on its circumference.

12. Diameter

The distance across a circle, passing through its center. It is twice the length of the radius.

By memorizing these essential terms, you will not only enhance your understanding of the subject but also improve your ability to approach problems with a clear and structured mindset. These terms are the building blocks for more complex topics, and mastering them is key to success.

How to Interpret Diagrams in Geometry

Understanding diagrams is crucial for solving problems accurately and efficiently. These visual representations provide insights into the relationships between different elements and help you visualize complex concepts. By interpreting diagrams correctly, you can often identify key properties and use them to guide your problem-solving process.

Focus on Key Elements

Start by identifying the most important components of the diagram, such as points, lines, angles, and shapes. Pay attention to any labels, as these can provide crucial information about the dimensions or relationships between different elements. Understanding the context of each label is essential for interpreting the diagram correctly.

Look for Relationships and Symmetry

Diagrams often highlight symmetries or specific geometric properties, such as parallel lines, perpendicular lines, or congruent shapes. Identifying these patterns can help you make inferences about the properties of the diagram and simplify problem-solving. For example, if two lines are marked as parallel, you know they will never intersect, which can be useful in angle calculations.

In addition, focus on any given measurements such as lengths, angles, or areas. These numbers can often be used directly in your calculations. Some diagrams may include additional markers like arcs or tick marks to indicate specific properties, such as equal sides or angles. Understanding these markings is essential for interpreting the diagram correctly and applying the right formulas.

By developing a strategy for analyzing diagrams, you will be better equipped to extract valuable information and apply it to solve problems efficiently. With practice, interpreting visual data will become second nature, making it easier to tackle complex questions and avoid mistakes.

Common Geometry Question Formats

In any assessment related to shapes, angles, and spatial reasoning, there are several common types of questions that test your understanding. These questions are designed to assess your ability to apply concepts in practical scenarios, whether it’s through calculations, visual analysis, or logical deductions. Recognizing the formats of these questions can help you approach them confidently and efficiently.

Problem-Solving and Calculation Questions

These questions typically ask you to calculate measurements such as the area, perimeter, volume, or angles of a given figure. They require a solid understanding of formulas and the ability to apply them to specific shapes and situations. These questions may provide a diagram and ask you to solve for unknown values using the properties of the shape.

Proof-Based Questions

Proof questions require you to demonstrate a logical sequence of statements and reasons to establish a conclusion. They might ask you to prove that two shapes are congruent, that two angles are equal, or that a certain property holds true for a given figure. These questions test both your reasoning abilities and your knowledge of geometric theorems.

Conceptual and Theoretical Questions

These questions may not require detailed calculations but focus on your understanding of concepts and definitions. You might be asked to identify properties of shapes, explain relationships between different geometric elements, or describe how specific concepts apply in real-world situations.

Visual Interpretation Questions

In this format, you are given a diagram or figure and asked to interpret it. Questions may ask you to identify specific components such as lines, angles, or shapes, or to explain how certain geometric properties apply to the diagram. Diagrams may also be accompanied by measurements or conditions, which you must analyze and use in your responses.

Multiple-Choice or Short Answer Questions

Multiple-choice questions typically present a question with several possible answers, and you must choose the correct one. These questions are often used to test your knowledge of basic concepts, definitions, and simple calculations. Short-answer questions may ask for brief explanations or specific numerical answers.

Question Type	Key Focus	Examples
Problem-Solving	Calculation of area, perimeter, volume, angles	Find the area of a circle with radius 5 cm
Proof-Based	Logical reasoning and theorems	Prove that two triangles are congruent
Conceptual	Understanding definitions and properties	What is the difference between a rectangle and a rhombus?
Visual Interpretation	Diagram analysis and application	Identify parallel lines in a given diagram
Multiple-Choice	Basic knowledge or quick calculation	What is the sum of the interior angles of a triangle?

Familiarizing yourself with these common question formats will help you manage time and resources efficiently during your assessments. By practicing each type, you will improve both your speed and accuracy, ensuring a well-rounded understanding of the material.

How to Check Your Answers Quickly

Verifying your solutions efficiently is a critical skill during any test. The ability to quickly identify potential mistakes and confirm the accuracy of your work can save valuable time and boost your confidence. Here are some strategies to help you check your responses thoroughly but swiftly.

1. Review Your Calculations

After solving a problem, go through your calculations quickly but carefully. Check if all arithmetic operations were performed correctly, and ensure you haven’t made simple errors like skipping a step or misreading a value. Sometimes, recalculating key figures, such as areas or angles, can reveal overlooked mistakes.

2. Verify Units and Dimensions

Always ensure that you have applied the correct units for measurements. It’s easy to forget to include units like centimeters or degrees, which can lead to confusion. Double-check that each part of your solution is expressed consistently with the appropriate units of measurement.

3. Use Estimation as a Check

Roughly estimating the result before you start calculating can give you a reference point for comparison. If your final answer seems drastically different from your initial estimate, it’s a red flag that something might be wrong. A quick mental check can often help spot major errors.

4. Cross-Check with Known Properties

Make sure your results align with well-known principles. For example, if you’re working with triangles, check if the sum of the angles equals 180 degrees. For circles, make sure the radius, circumference, and area relate to each other appropriately. Verifying these basic relationships can quickly highlight any inconsistencies.

5. Double-Check Diagrams and Labels

If the problem includes a diagram, make sure you’ve referenced it correctly throughout the problem. Check that all labels match the values used in your calculations. Misinterpreting a diagram or missing a label can lead to incorrect answers, so a final look at the visual aid is always beneficial.

6. Set Aside Time for Final Review

Once you’ve completed all the questions, allocate the last few minutes of your test to review your work. This buffer time is essential for catching mistakes you might have missed in the rush of completing the problems. Use it to confirm calculations, verify logical steps, and ensure no details were overlooked.

Incorporating these quick checks into your routine will help you improve the quality of your work without compromising your time management. By practicing these strategies regularly, you’ll develop the skill to identify errors efficiently and approach assessments with greater confidence.

Using Resources for Better Results

Accessing the right materials and tools can significantly improve your performance and understanding. Leveraging available resources effectively can help clarify complex concepts, sharpen your skills, and boost your confidence. Here are several ways to make the most of the resources at your disposal.

1. Online Tutorials and Videos

There are numerous platforms offering free video lessons that break down challenging topics into manageable steps. These tutorials often use visual aids and real-life examples to help reinforce learning. Watching a concept explained from a different perspective can often lead to better comprehension and quicker mastery of the material.

2. Interactive Practice Websites

Interactive websites and apps allow you to practice various problems at your own pace. These resources provide instant feedback, which can help you identify errors and correct them immediately. By repeating exercises and gradually increasing difficulty levels, you can develop problem-solving strategies and improve your speed and accuracy.

3. Textbooks and Study Guides

Using well-established textbooks and study guides is a great way to reinforce key concepts. These resources often contain step-by-step solutions, examples, and practice questions, which help clarify difficult topics. Make sure to read the explanations thoroughly and work through practice problems to strengthen your knowledge base.

4. Flashcards for Key Terms

Flashcards are an excellent way to memorize important definitions, formulas, and properties. By reviewing them regularly, you can internalize essential concepts and recall them quickly when needed. You can either create your own flashcards or find online versions that cover the key points of your study material.

5. Study Groups and Peer Discussions

Collaborating with classmates in study groups can provide different perspectives and solutions to problems. Explaining concepts to peers helps solidify your own understanding while also allowing you to learn from their methods and insights. Sometimes, a peer’s explanation can make an unclear concept easier to grasp.

6. Tutoring and Extra Help

If you find yourself struggling with specific topics, consider seeking additional support from a tutor. Tutors can provide personalized guidance and help you focus on areas that need improvement. Many schools offer free tutoring sessions, or you can explore online tutoring services for flexible options.

By actively using these resources, you can enhance your understanding, retain information more effectively, and tackle challenges with greater ease. Consistency and utilizing a variety of learning tools will help you perform at your best and achieve better results.

Preparing for Advanced Topics

As you progress in your studies, you will encounter more complex and abstract concepts that build upon the foundational knowledge you have already acquired. These advanced topics often require a deeper understanding of principles, more problem-solving skills, and the ability to apply various strategies to new situations. Here’s how you can effectively prepare for these challenges and excel in higher-level material.

1. Master the Basics

Before diving into more complex topics, ensure you have a solid grasp of fundamental concepts. The ability to quickly recall basic properties and relationships between shapes will serve as a strong foundation for tackling advanced problems. Review key definitions, theorems, and formulas that are frequently used in higher-level material.

2. Strengthen Problem-Solving Techniques

Advanced topics often present problems that require creative approaches. Practice breaking down complex problems into simpler steps, identifying patterns, and applying multiple methods to find solutions. Working through various types of problems will increase your flexibility and adaptability in handling new challenges.

3. Focus on Proofs and Logic

Many advanced concepts rely heavily on logic and proofs. Strengthen your reasoning skills by practicing proof-based questions regularly. Understanding the structure of a proof and how to logically justify each step is crucial for tackling more difficult material. Make sure to review different types of proofs, such as direct, indirect, and proof by contradiction.

4. Use Visual Aids and Diagrams

When dealing with more abstract concepts, visualizing problems can help clarify complex relationships. Learn how to effectively sketch diagrams and use them to support your reasoning. Diagrams are essential tools for understanding spatial relationships and can make abstract ideas more concrete.

5. Engage with Advanced Study Resources

Seek out study materials specifically designed for advanced topics. Textbooks, online courses, and scholarly articles often contain in-depth explanations and additional examples that will deepen your understanding. Don’t be afraid to explore resources outside of your curriculum to gain a broader perspective.

By consistently practicing, reinforcing your understanding of the basics, and engaging with advanced study resources, you will be well-equipped to handle the challenges of more complex material. Preparation is key to success, and with dedication and focus, you can confidently tackle even the most difficult topics.