Algebra 2 Final Exam Answer Key 2025

Preparing for a significant mathematics test requires a solid understanding of key concepts and the ability to apply them under pressure. Whether you’re dealing with complex equations, functions, or various types of expressions, mastering these skills can make all the difference. This guide offers a comprehensive approach to navigating the crucial problems that typically appear on such assessments.

Students often face challenges when it comes to understanding how different topics interconnect. This resource will provide clear explanations, helpful hints, and methods to solve problems efficiently. With practice and the right strategies, it’s possible to tackle even the toughest questions with confidence.

Focus on the areas that require the most attention and refine your problem-solving techniques. Success in this subject depends not only on memorization but also on a deep comprehension of how to approach diverse types of problems logically.

Mathematics Assessment Solutions Guide

Successfully navigating through an advanced mathematics test requires not only knowledge but also the ability to apply learned concepts in practical ways. This section provides a breakdown of problem-solving strategies, showcasing common problem types that often appear in these assessments. Understanding the solutions to these problems can enhance your readiness and boost your confidence.

Detailed Breakdown of Solutions

In this part, we’ll walk through a variety of problems and demonstrate how to approach them step-by-step. Whether you are dealing with complex equations or analyzing functions, each solution is designed to highlight the logical reasoning behind it. Mastering these techniques will allow you to handle similar challenges with greater efficiency during the actual test.

Improving Problem-Solving Skills

Effective problem-solving goes beyond simply knowing the right formula; it’s about understanding when and how to apply it. Practice is key, and using this resource to go over solutions will help you recognize patterns, spot common pitfalls, and develop a more intuitive approach to solving complex questions.

Overview of Mathematics Assessment Format

Understanding the structure of a major mathematics assessment is essential for effective preparation. This section will provide insights into the general layout and types of questions that students are likely to encounter. Familiarizing yourself with the format will help manage time more efficiently and reduce anxiety on the day of the test.

Key Components of the Assessment

The assessment is typically divided into several sections, each focusing on different mathematical concepts. These sections may vary in terms of difficulty, with some requiring more complex problem-solving techniques. Below is a breakdown of what you can expect:

Section	Content Focus	Question Type
Section 1	Equations and Inequalities	Multiple Choice, Short Answer
Section 2	Functions and Graphing	Graph Interpretation, Word Problems
Section 3	Polynomials and Rational Expressions	Long Answer, Step-by-Step Solutions
Section 4	Exponents and Logarithms	Multiple Choice, Problem Solving

Time Allocation and Strategy

Each section is allocated a specific amount of time, and it is important to pace yourself accordingly. The first few questions in each section are typically less difficult, while later ones become more complex. A good strategy is to start with the questions you find easiest and return to more challenging ones later.

Key Topics Covered in Mathematics Assessment

To succeed in a mathematics test, it is essential to have a firm grasp on the main topics that are frequently tested. These areas form the foundation for most questions and understanding them deeply will increase your chances of performing well. This section highlights the core concepts you should focus on while preparing.

Important Mathematical Concepts

Several critical concepts are central to the assessment. These topics not only appear frequently but also require a solid understanding of both theory and application. The main areas include:

• Quadratic Equations – Solving, factoring, and graphing.
• Polynomials – Operations, long division, and synthetic division.
• Functions and Graphs – Identifying different types of functions and interpreting graphs.
• Rational Expressions – Simplifying and solving equations involving rational numbers.
• Logarithms and Exponents – Understanding properties and solving related problems.

Advanced Problem-Solving Techniques

Beyond the basics, there are also more complex areas of study that can challenge students. Topics such as systems of equations, matrices, and complex numbers are essential for solving higher-level problems. Mastery of these concepts is often required to tackle the most difficult questions in the test.

How to Use the Solutions Guide Effectively

While reviewing a solutions guide can be helpful, it’s important to approach it strategically. Simply looking at the final results isn’t enough; understanding how to reach those results is key to improving your problem-solving skills. This section outlines how to maximize the value of the provided solutions.

Step-by-Step Review Process

To use the guide effectively, follow a structured approach to fully grasp the reasoning behind each solution:

1. Attempt the problem first: Try to solve the problem on your own before checking the solution. This will help identify any gaps in your understanding.
2. Compare your approach: Look at how your method aligns with the provided solution. Pay attention to any differences in techniques used.
3. Focus on the steps: Study each step carefully. Ensure you understand why each action is taken and how it leads to the final result.
4. Identify common errors: If your solution differs from the provided one, analyze where you went wrong and learn from your mistakes.

Effective Strategies for Improvement

Using a solutions guide can be more than just a way to check your work. It’s an opportunity to improve your mathematical skills. Here are some strategies to consider:

• Work through similar problems: After reviewing the solution, try solving similar problems on your own to reinforce the concept.
• Take notes: Write down any techniques or shortcuts that you find particularly helpful. These notes will be useful for future reference.
• Ask questions: If a step or concept doesn’t make sense, seek clarification either from your instructor, a peer, or additional resources.

Common Mistakes in Mathematics Assessments

When preparing for a challenging mathematics test, students often fall into certain traps that can lead to avoidable errors. These mistakes are typically due to misunderstandings of key concepts, rushed work, or overlooked details. Recognizing these common pitfalls can help improve performance and avoid missteps during the actual test.

Mistake	Cause	How to Avoid
Misinterpreting the problem	Failure to read the question carefully	Take time to understand what is being asked before starting to solve.
Sign errors	Not paying attention to negative signs	Double-check signs before moving to the next step.
Forgetting to factor completely	Overlooking the need for full factoring	Check all terms for common factors before simplifying.
Rushing through calculations	Trying to finish too quickly	Take time to check each calculation carefully.
Not showing work	Skipping steps or doing mental math	Always write out each step to prevent errors and to check work.

By recognizing these common mistakes and understanding their causes, students can take proactive measures to avoid them. Being mindful of the details and practicing careful work habits will help reduce errors and improve overall performance in mathematics assessments.

Strategies for Studying Mathematics

Effective preparation for a mathematics assessment requires more than just reviewing notes. It involves actively engaging with the material, practicing problem-solving techniques, and honing critical thinking skills. The following strategies can help you maximize your study time and improve your performance in the subject.

Active Learning Techniques

Rather than passively reading through textbooks, focus on interactive learning methods. These approaches can help reinforce concepts and improve retention:

• Practice regularly: Solve a variety of problems consistently to strengthen your understanding and identify areas needing improvement.
• Teach someone else: Explaining concepts to others can help solidify your own understanding and reveal gaps in knowledge.
• Use study aids: Leverage online resources, video tutorials, and practice tests to expose yourself to different teaching methods.
• Work in groups: Collaborating with peers can provide different perspectives on solving problems and offer helpful tips.

Focused Review Sessions

To make the most of your study time, focus on the following key review strategies:

1. Prioritize difficult topics: Spend extra time on the areas where you struggle the most, whether it’s functions, equations, or graphing.
2. Break down complex problems: Split complicated problems into smaller, more manageable steps to avoid feeling overwhelmed.
3. Use spaced repetition: Review material multiple times over increasing intervals to improve long-term retention.
4. Practice under timed conditions: Simulate test conditions by solving problems within a set time limit to improve speed and accuracy.

By incorporating these strategies into your study routine, you can better prepare yourself for challenges and enhance your understanding of complex mathematical concepts.

Understanding Mathematics Equations

Equations are the foundation of much of the material covered in higher-level mathematics. They represent relationships between variables and constants, and solving them is essential for understanding complex concepts. This section focuses on the importance of equations and offers guidance on how to approach them effectively.

Equations can take many forms, ranging from simple linear expressions to more complex polynomial and rational forms. Each type has its own set of rules and techniques for finding solutions. Understanding how to manipulate these equations is crucial for progressing in the subject and solving a wide variety of problems.

One of the most important skills when working with equations is recognizing the structure and identifying the correct method for solving. Whether you are dealing with a quadratic equation, a system of linear equations, or an exponential equation, knowing how to apply the right strategies will greatly improve your ability to solve problems efficiently and accurately.

Solving Quadratic Equations in Detail

Quadratic equations are a fundamental type of mathematical expression that appears frequently in higher-level problems. They involve variables raised to the second power and can be solved using various methods. Mastering these techniques is essential for progressing in the subject and for solving more complex problems. In this section, we will explore the most common methods used to solve quadratic equations.

Methods for Solving Quadratics

There are several approaches to solving quadratic equations, each suited for different types of problems. The most commonly used methods include:

• Factoring: This method involves rewriting the quadratic equation as a product of two binomials. It is useful when the equation is easily factorable.
• Completing the Square: This technique involves manipulating the equation to form a perfect square trinomial, making it easier to solve for the variable.
• Quadratic Formula: The quadratic formula is a universal method that works for all quadratic equations. It involves plugging values into a formula to find the solutions directly.
• Graphing: By graphing the equation, you can visually find the points where the curve intersects the x-axis, which correspond to the solutions of the equation.

Step-by-Step Example

Let’s walk through an example of solving a quadratic equation using the quadratic formula:

1. Start with the quadratic equation in standard form: ax² + bx + c = 0.
2. Identify the coefficients: a, b, and c.
3. Substitute these values into the quadratic formula: x = (-b ± √(b² – 4ac)) / 2a.
4. Simplify the expression under the square root (the discriminant) to check for real solutions.
5. Calculate the values of x by evaluating the formula for both the plus and minus options.

By following these steps, you can solve any quadratic equation, whether it can be factored easily or requires the use of the quadratic formula.

Polynomials and Their Applications

Polynomials are expressions that involve sums of powers of variables, each multiplied by a constant coefficient. These mathematical forms are essential for modeling real-world situations and understanding complex systems. From simple equations to more intricate models, polynomials provide a versatile tool for solving problems across various fields.

Understanding polynomials is crucial, as they are used to represent many types of functions. Whether describing the trajectory of an object in motion, optimizing business profits, or analyzing the behavior of financial models, polynomials serve as a foundation for numerous applications in science, engineering, and economics.

Real-World Applications of Polynomials

Polynomials are applied in many different areas, with some of the most common applications including:

• Physics: Polynomials are used to model the motion of objects, such as the path of a projectile or the oscillation of a spring.
• Economics: Polynomials help to analyze supply and demand curves, as well as model economic growth or decay.
• Engineering: Engineers use polynomial equations in the design of structures and systems, such as calculating stress, strain, or fluid dynamics.
• Statistics: Polynomial regression is used to model relationships between variables and make predictions based on data sets.

Solving Polynomial Equations

One of the primary methods for solving polynomial equations is factoring. For higher-degree polynomials, other techniques, such as synthetic division or using the Rational Root Theorem, may be necessary. Understanding how to manipulate polynomials effectively allows you to find solutions and make predictions with greater accuracy.

By mastering polynomials and their applications, students can apply these concepts to solve real-world problems in fields ranging from physics to economics and beyond.

Functions and Graphing in Mathematics

In mathematics, functions are essential tools used to describe relationships between variables. By analyzing how one variable changes in response to another, we can gain deeper insights into various systems and behaviors. Graphing these relationships visually helps us understand patterns, trends, and the behavior of functions over a range of values. This section delves into the importance of functions and the methods used to graph them accurately.

Graphing is a powerful tool for visualizing mathematical concepts. It transforms abstract equations into clear, understandable diagrams. By understanding how to graph different types of functions, students can interpret data, predict outcomes, and solve problems in fields ranging from engineering to economics.

Types of Functions and Their Graphs

There are several types of functions, each with its own distinct graph. Here are some of the most commonly studied functions:

• Linear Functions: These functions produce straight lines when graphed and are described by the equation y = mx + b, where m is the slope and b is the y-intercept.
• Quadratic Functions: These create parabolic curves and are represented by equations of the form y = ax² + bx + c. They are often used to model projectile motion and optimization problems.
• Cubic Functions: These functions result in curves with one or two inflection points, and their equations are in the form y = ax³ + bx² + cx + d.
• Exponential Functions: These functions exhibit rapid growth or decay and are used to model population growth, radioactive decay, and financial interest rates.

Graphing Techniques

Graphing a function requires understanding its general behavior and properties. Some key steps include:

1. Identify the function type: Determine whether the function is linear, quadratic, exponential, etc., as this will inform the shape of the graph.
2. Plot key points: Find the x- and y-intercepts, vertex, and other significant points, then plot them on the coordinate plane.
3. Draw the graph: Connect the points smoothly, respecting the overall behavior of the function. For quadratic functions, ensure that the curve is symmetric around the vertex.

By mastering graphing techniques and understanding different functions, students can better analyze relationships between variables and solve complex problems with confidence.

Rational Expressions Simplification

Simplifying rational expressions is an important skill in mathematics, as it allows us to make complex expressions easier to work with and understand. A rational expression is a fraction where both the numerator and the denominator are polynomials. By simplifying these expressions, we can identify key characteristics, such as asymptotes or intercepts, and make calculations more manageable.

To simplify a rational expression, the goal is to cancel out any common factors between the numerator and the denominator. This process involves factoring both parts of the fraction and reducing it to its simplest form. The simplification process not only makes the expression more compact but also helps in solving problems more efficiently.

Steps for Simplification

Follow these steps to simplify a rational expression:

1. Factor both the numerator and denominator: Look for common factors and factor each polynomial fully.
2. Cancel common factors: If a factor appears in both the numerator and denominator, eliminate it, as long as it’s not zero.
3. Rearrange the expression: Once simplified, rewrite the expression in its simplest form, ensuring no factors remain that can be reduced further.

Common Pitfalls in Simplification

While simplifying rational expressions, there are some common mistakes to avoid:

• Forgetting to factor completely: Make sure both the numerator and denominator are fully factored before canceling out terms.
• Dividing by zero: Always ensure that the cancelled factor does not result in division by zero, as this is undefined.
• Misidentifying factors: Be cautious when factoring more complex polynomials, as incorrect factoring can lead to mistakes in the simplification process.

By following the correct steps and avoiding common errors, you can simplify rational expressions with confidence and solve problems more effectively.

Working with Logarithms and Exponents

Understanding the relationship between logarithms and exponents is a fundamental aspect of mathematics. These concepts are closely connected, and mastering them is crucial for solving a wide range of problems. Logarithmic and exponential functions are often used to model real-world phenomena, such as population growth or compound interest, and they appear frequently in advanced math courses.

Exponents represent repeated multiplication of a number by itself, while logarithms are the inverse operation, answering the question “to what power must a base be raised to produce a given number?” Being proficient with these two operations enables students to manipulate and simplify expressions, solve equations, and apply these tools in various problem-solving scenarios.

Key Properties of Logarithms and Exponents

Both logarithmic and exponential expressions have several important properties that help in simplifying and solving equations. Some of the key properties include:

Property	Description
Product Rule	For exponents: (a^m cdot a^n = a^{m+n}). For logarithms: (log_b(x) + log_b(y) = log_b(xy)).
Quotient Rule	For exponents: (a^m / a^n = a^{m-n}). For logarithms: (log_b(x) – log_b(y) = log_b(x/y)).
Power Rule	For exponents: ((a^m)^n = a^{m cdot n}). For logarithms: (log_b(x^n) = n cdot log_b(x)).

Applications of Logarithms and Exponents

Logarithmic and exponential functions are not just theoretical concepts–they are used extensively in real-world applications. Here are a few examples:

• Exponential growth and decay: These concepts model natural processes such as population growth, radioactive decay, and interest accumulation.
• Solving equations: Logarithms are often used to solve equations where the variable appears in an exponent, such as in growth or decay problems.
• Computer science: Exponentiation and logarithmic functions are used in algorithms, cryptography, and data structure analysis.

By mastering the rules and applications of logarithms and exponents, students gain powerful tools for both solving complex problems and understanding mathematical relationships in the world around them.

Understanding Systems of Equations

Systems of equations are a collection of two or more equations that share common variables. The goal when working with these systems is to find the values of the variables that satisfy all the equations simultaneously. These systems arise naturally in a wide variety of contexts, from solving word problems in mathematics to modeling real-world situations such as supply and demand, physics, and engineering.

To solve a system of equations, you typically employ different methods such as substitution, elimination, or graphing. Each method has its advantages depending on the type of system and the context in which it is used. Whether you are solving linear or nonlinear systems, understanding the relationships between the equations and the variables is key to finding the correct solution.

Methods for Solving Systems of Equations

There are several approaches that can be used to solve a system of equations. Below are the most common methods:

• Substitution Method: This technique involves solving one equation for one variable and then substituting that expression into the other equation. It is particularly useful when one equation is easy to solve for one variable.
• Elimination Method: Also known as the addition method, this approach involves adding or subtracting the equations to eliminate one of the variables. It is most effective when the coefficients of one of the variables are already equal or can easily be made equal.
• Graphing Method: This method involves plotting the equations on a graph and finding the point where the lines or curves intersect. This point represents the solution to the system. This method is ideal for visualizing solutions but may be less accurate if the intersection does not occur at integer values.

Applications of Systems of Equations

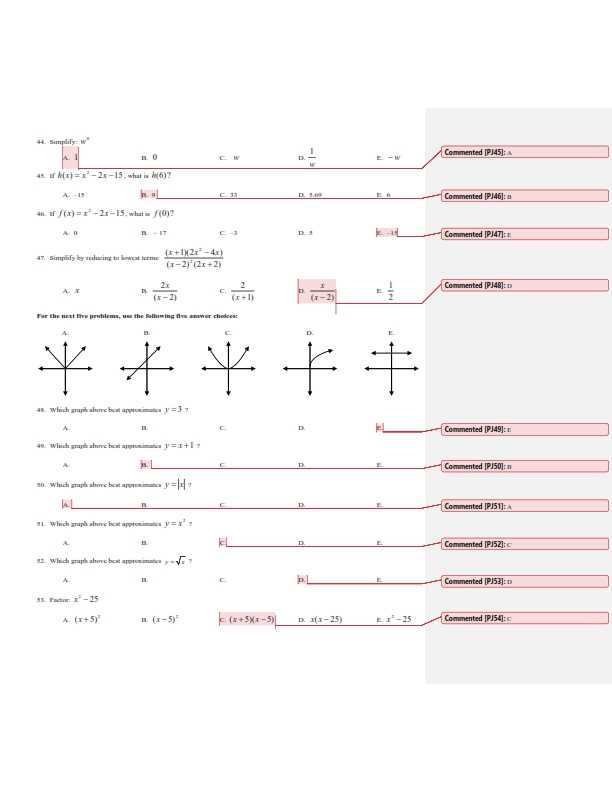
Systems of equations are widely used in various fields to solve problems involving multiple variables. Some common applications include:

• Economics: Systems of equations are used to model supply and demand, pricing strategies, and economic equilibrium.
• Physics: They are used to solve problems involving multiple forces acting on an object, or when analyzing electrical circuits with multiple components.
• Engineering: In engineering, systems of equations help solve problems related to structural integrity, material properties, and fluid dynamics.

By mastering the techniques for solving systems of equations, students gain essential skills for tackling a wide range of mathematical and real-world challenges.

Examining Inequalities and Absolute Values

Inequalities and absolute values are fundamental concepts that help describe relationships between numbers and their magnitudes. Inequalities represent situations where one value is larger or smaller than another, often used to define ranges or restrictions on variables. Absolute value, on the other hand, deals with the distance of a number from zero, regardless of direction, and plays a crucial role in solving equations and inequalities involving magnitudes or distances.

Understanding how to manipulate and solve inequalities and absolute values is essential for tackling a wide range of mathematical problems, from simple comparisons to more complex applications in real-world scenarios. Whether analyzing budgets, measurements, or constraints in engineering, these concepts provide a way to work with conditions that are not always precise or equal.

Solving Inequalities

Inequalities can be solved in a similar manner to equations, but with a few important differences, especially when multiplying or dividing by negative numbers. The direction of the inequality sign must be reversed when performing these operations. Some key steps to solving inequalities include:

• Isolate the variable: Just like solving an equation, the goal is to get the variable on one side of the inequality by performing inverse operations.
• Flip the inequality: If you multiply or divide by a negative number, remember to flip the inequality sign.
• Graph the solution: Inequalities are often represented graphically on a number line, showing the range of solutions.

Working with Absolute Values

Absolute value refers to the magnitude of a number, regardless of whether it is positive or negative. It is represented by two vertical bars around the number, such as |x|. The absolute value of a number is always non-negative, and it is crucial in solving equations and inequalities that involve distance or magnitude. Here’s how to work with absolute values:

• Absolute value equations: To solve equations involving absolute values, consider both the positive and negative scenarios that could result in the given magnitude.
• Absolute value inequalities: When dealing with absolute value inequalities, break them into two separate cases–one for the positive side and one for the negative side–to account for all possible solutions.

By mastering these techniques, you can confidently solve problems that involve comparing quantities, defining constraints, and working with distance or magnitude in both theoretical and practical contexts.

Tips for Time Management on Exams

Effective time management during assessments is essential for maximizing performance and minimizing stress. The ability to allocate the right amount of time to each section of the test ensures that all questions are addressed, and it helps avoid rushing through critical parts. Proper planning can make a significant difference in how you approach your test and the quality of your responses.

Start by assessing the structure of the test. Understand the number of questions, the type of questions, and their weight. This will give you a clear idea of where to spend more time and where to move quickly. Prioritizing tasks based on their complexity and point value will help you make the most efficient use of your time.

• Allocate Time Wisely: Set a specific time limit for each section or question. Stick to it as closely as possible to ensure you don’t spend too much time on any one item.
• Practice Under Timed Conditions: Take practice tests with time constraints. This will help you get accustomed to the pressure and improve your speed without compromising accuracy.
• Skip and Return: If you encounter a challenging question, skip it temporarily and move on to the next one. Return to it later with a fresh perspective.
• Don’t Rush the First Question: While it’s important to move quickly, don’t rush through the first questions of the test. Starting strong will give you confidence and set the tone for the rest of the assessment.
• Keep Track of Time: Regularly check the clock to ensure that you are progressing at the appropriate pace. Set milestones (e.g., halfway through the test at the 50-minute mark) to keep yourself on track.

By implementing these strategies, you can enhance your ability to manage your time effectively during an assessment, ensuring that you complete every section thoughtfully and within the allotted time. Remember, preparation and practice are key to becoming efficient under time pressure.

What to Expect on the 2025 Assessment

As the year progresses, it’s important to understand what will be expected during the upcoming assessment period. This includes the types of problems you will encounter, the format of the test, and how you can best prepare for a successful performance. By knowing what lies ahead, you can approach the test with confidence and clarity, ensuring that you’re fully equipped to handle the challenges.

The upcoming assessment is designed to evaluate your understanding of a wide range of mathematical concepts, from basic operations to more advanced topics. Expect a mixture of problem types, including multiple-choice questions, short answer responses, and detailed problem-solving exercises. Each section will require not only accuracy but also the ability to apply knowledge in practical situations.

Types of Questions

The test will likely include a combination of theoretical questions and real-world application problems. The goal is to test your ability to reason mathematically and solve complex problems efficiently.

• Multiple Choice: Quick, straightforward questions that test your recall and basic understanding.
• Short Answer: Problems that require a step-by-step approach to demonstrate your process and reasoning.
• Application Problems: Real-world scenarios where you’ll need to apply mathematical principles to solve practical issues.

Preparation Tips

To succeed on the assessment, it’s crucial to review all covered materials thoroughly. Focus on understanding concepts rather than memorizing formulas. Practicing sample problems under timed conditions can help you improve your speed and accuracy. Be sure to also familiarize yourself with the types of questions that will appear so you can approach each one with a clear strategy.

By understanding the structure and expectations of the test, you’ll be better prepared to tackle each section and manage your time efficiently. Whether you’re working on calculations or problem-solving, the key is consistent practice and a solid grasp of the fundamental concepts.

Using Practice Tests for Preparation

One of the most effective strategies for getting ready for any assessment is utilizing practice tests. These resources simulate the actual testing environment, allowing you to familiarize yourself with the types of questions, the time constraints, and the overall format. By integrating practice tests into your study routine, you can improve your problem-solving skills and boost your confidence for the upcoming challenge.

Taking practice tests not only helps you assess your current understanding, but it also identifies areas where you may need further improvement. This targeted approach allows you to focus your energy on the topics that require more attention, ensuring that you are thoroughly prepared for each section of the assessment.

Benefits of Practice Tests

Here are some key benefits of using practice tests in your preparation:

• Familiarity with Format: Practice tests help you get used to the structure and types of questions you will encounter, reducing anxiety during the actual assessment.
• Time Management: Completing a practice test under timed conditions allows you to gauge how well you can manage your time and helps you prioritize questions efficiently.
• Identify Weaknesses: Practice tests reveal areas where your understanding may be lacking, so you can focus on strengthening those topics before the test.
• Build Confidence: Consistent practice increases familiarity with the material, which boosts your confidence and reduces pre-assessment stress.

Maximizing Your Practice Test Experience

To get the most out of your practice tests, consider the following strategies:

1. Simulate Real Test Conditions: Take the test in a quiet environment, with the same time limits and without any outside help, to replicate the actual testing experience.
2. Review Your Mistakes: After completing a practice test, go over the questions you got wrong. Understand why the correct answer is what it is and review any relevant concepts.
3. Take Multiple Tests: The more practice tests you complete, the more you will refine your problem-solving techniques and improve your performance under pressure.

Incorporating practice tests into your study routine is an excellent way to assess your readiness, identify weak points, and boost your overall preparedness for the upcoming assessment. By familiarizing yourself with the test format and improving your time management skills, you’ll increase your chances of success and approach the challenge with confidence.

Reviewing Concepts Before the Test

Before tackling any major assessment, it’s essential to review and reinforce the foundational concepts you’ve learned. This stage of preparation allows you to refresh your memory, solidify your understanding, and identify any gaps in knowledge. Whether it’s revisiting specific problem-solving methods or clarifying theoretical ideas, thorough review ensures that you approach the test with confidence and readiness.

A comprehensive review helps you mentally organize the material and boosts recall under pressure. It also encourages you to focus on the most important topics while ensuring that no key concepts are overlooked. By following an organized review plan, you can maximize your study time and enhance your performance.

Effective Review Strategies

Here are some strategies to guide your review sessions:

• Break Down Complex Topics: Divide complicated topics into smaller, manageable sections. Tackle each one individually to prevent feeling overwhelmed.
• Use Study Aids: Leverage practice problems, flashcards, and study guides to reinforce your understanding. These resources help solidify your knowledge and highlight areas that need more attention.
• Focus on Problem-Solving Techniques: Ensure that you are comfortable with the methods for solving equations and tackling word problems. Practice different types of problems to become adept at applying your knowledge in various scenarios.
• Take Breaks: Short, regular breaks during review sessions can help maintain focus and prevent burnout. A rested mind retains information more effectively.

Prioritizing Key Topics

While reviewing, it’s important to prioritize the most critical concepts that are likely to appear on the assessment. These key areas might include:

1. Functions and Graphing: Understanding the behavior and properties of functions is crucial for solving many problems. Make sure to practice graphing and interpreting different types of functions.
2. Equations and Inequalities: Ensure you are comfortable with solving linear, quadratic, and higher-order equations, as well as inequalities and systems of equations.
3. Rational Expressions and Polynomials: Master simplifying and solving rational expressions and polynomial equations, as these are common and essential topics.
4. Logarithms and Exponents: Review the laws and rules governing exponents and logarithmic functions to handle complex expressions with ease.

By concentrating your efforts on these key areas and applying effective review techniques, you’ll improve your readiness and ensure that you approach the test with clarity and confidence.