Statistics Final Exam Questions and Answers

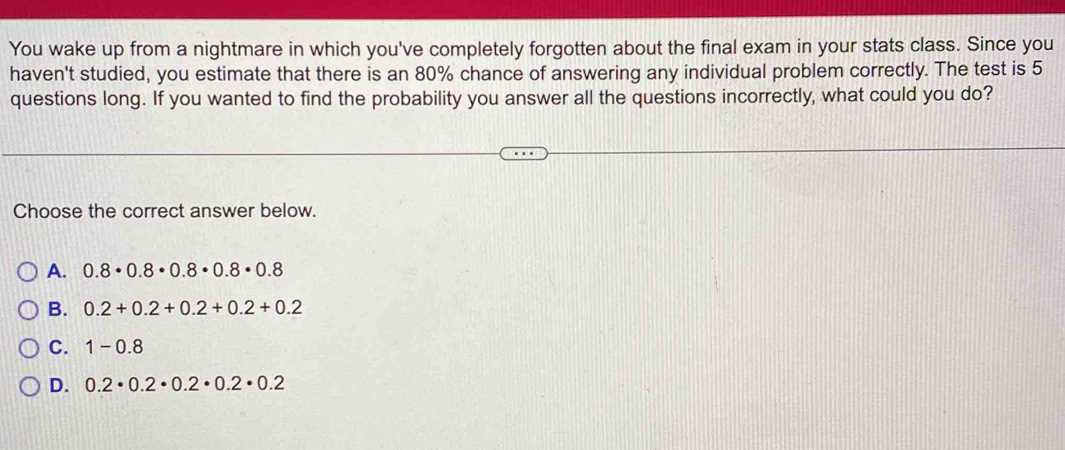
Successfully navigating through complex numerical problems requires a clear understanding of core principles. Whether you are facing a classroom challenge or preparing for a professional evaluation, a solid foundation in mathematical concepts is essential for achieving the best results. This guide will equip you with the necessary tools to approach different types of problems with confidence and precision.

Preparation is the key to success, especially when dealing with topics that involve data analysis, probability, and various computational methods. By focusing on fundamental techniques and practicing regularly, you can significantly improve your performance. Familiarity with different problem formats, as well as the application of theoretical knowledge, will allow you to quickly identify the most effective solution paths.

To perform well under pressure, it is important to not only understand the material but also to develop strategies that help in time management. With a structured approach and the right practice materials, you can ensure that you are well-prepared for any challenge that comes your way. Use this guide to build confidence, refine your problem-solving techniques, and ensure a thorough understanding of the subject matter.

Statistics Final Exam Questions and Answers

When preparing for a significant assessment, understanding the types of problems you will face can make all the difference. Focusing on key topics and ensuring that you can apply your knowledge to various scenarios will help you perform efficiently. Mastering these challenges requires both theoretical comprehension and practical application. This section outlines essential practices and techniques for tackling different types of mathematical problems that commonly appear in comprehensive evaluations.

Essential Topics to Focus On

Familiarize yourself with core concepts such as probability theory, hypothesis testing, data interpretation, and regression analysis. Each area presents unique problem formats that require specific approaches. By practicing these types of problems regularly, you will gain familiarity with the logic and methods needed to solve them quickly and accurately. Pay special attention to the most commonly tested concepts and ensure that you can work through problems without hesitation.

Effective Strategies for Success

Being well-prepared is not only about knowing the material but also about approaching problems strategically. Start by reviewing sample questions, focusing on both the methodology and the logical steps involved in solving each one. Time management plays a crucial role during the assessment. Practicing under timed conditions can help you gauge your ability to solve problems efficiently. Always double-check your work, especially when dealing with calculations or interpretation of results, to avoid careless errors.

Commonly Asked Questions in Statistics

When preparing for a major assessment, it is crucial to understand the types of challenges that are frequently presented. Familiarizing yourself with recurring problem formats allows you to develop an efficient problem-solving approach. In this section, we will explore the types of issues that are most commonly seen in comprehensive evaluations and provide strategies for tackling them effectively.

Probability-Based Problems

One of the most common areas involves dealing with probability scenarios, where you are asked to calculate the likelihood of specific events occurring under certain conditions. These problems often require a solid grasp of formulas and the ability to interpret given data correctly. It’s important to identify key values such as sample size, probability, and outcomes to determine the most accurate solutions.

Hypothesis Testing Challenges

Another frequently tested area involves hypothesis testing, where you must decide whether to accept or reject a given hypothesis based on statistical evidence. These problems typically require you to perform calculations and interpret results from various tests, such as t-tests or chi-square tests. Knowing when and how to use different tests based on the problem’s context is essential for success.

Key Concepts to Master for the Exam

To succeed in a comprehensive assessment, it is essential to have a strong grasp of fundamental ideas and methods that frequently appear in various problem formats. Mastering these core concepts will ensure that you are well-prepared to tackle a wide range of challenges efficiently. Focus on understanding both the theoretical foundations and their practical applications in solving real-world scenarios.

Key areas to concentrate on include understanding data distributions, performing calculations for confidence intervals, and analyzing relationships through regression techniques. Additionally, a firm grasp of probability principles, hypothesis testing procedures, and common testing methodologies will help you approach problems with confidence. Regular practice with problems that cover these core topics will build familiarity and improve accuracy during the assessment.

Understanding Statistical Distributions

A solid understanding of data distributions is crucial for solving problems that involve interpreting large sets of numerical information. These distributions describe how values are spread across a dataset and provide insights into underlying patterns. Grasping the characteristics of different distributions enables you to make more accurate predictions and decisions when analyzing data.

Types of Distributions to Know

Some of the most commonly encountered distributions include the normal distribution, binomial distribution, and Poisson distribution. Each type has its own properties and is used in different scenarios based on the nature of the data. Recognizing the type of distribution you are dealing with allows for more efficient analysis and decision-making.

Distribution	Key Characteristics	Common Applications
Normal	Symmetrical, bell-shaped, mean = median = mode	Height, weight, test scores
Binomial	Discreet outcomes, two possible results (success/failure)	Coin flips, survey responses
Poisson	Discreet, counts of events occurring in a fixed interval	Call center arrivals, traffic flow

Interpreting Distribution Graphs

Visual representations of distributions, such as histograms and probability density functions, are helpful tools for understanding the spread of data. These graphs allow you to quickly identify patterns such as skewness, outliers, and the central tendency of the dataset. Becoming familiar with these graphical tools is essential for accurate data interpretation in problem-solving situations.

How to Solve Hypothesis Testing Problems

Hypothesis testing is a fundamental process in determining whether there is enough evidence to support a specific claim or hypothesis about a population. The ability to perform these tests accurately is essential for drawing valid conclusions from data. In this section, we will explore the steps involved in solving such problems, from formulating hypotheses to making decisions based on statistical results.

To solve hypothesis testing challenges effectively, follow these steps:

Step 1: Define the Null and Alternative Hypotheses

Start by clearly defining two competing hypotheses: the null hypothesis, which represents no effect or difference, and the alternative hypothesis, which suggests a relationship or difference exists. The null hypothesis typically assumes that any observed difference is due to random chance, while the alternative hypothesis posits that the effect is real.

Step 2: Select the Significance Level

The next step is to choose a significance level (alpha), often set at 0.05. This represents the probability of rejecting the null hypothesis when it is actually true. The lower the significance level, the stronger the evidence required to reject the null hypothesis.

Step 3: Choose the Appropriate Test

Select the statistical test based on the data type and the hypotheses. Common tests include t-tests, chi-square tests, and ANOVA. Each test has specific assumptions, so it’s important to choose the one that fits your situation.

Step 4: Calculate the Test Statistic

Using the appropriate formula for the selected test, calculate the test statistic. This will help determine how far your sample data is from the hypothesized value. For example, in a t-test, you would calculate the t-value to compare the sample mean to the population mean.

Step 5: Make a Decision

Once the test statistic is calculated, compare it to the critical value from the statistical table or use the p-value to determine if the results are statistically significant. If the test statistic exceeds the critical value or the p-value is less than the significance level, you can reject the null hypothesis. Otherwise, you fail to reject it.

Step 6: Interpret the Results

Finally, interpret the results in the context of the problem. If you rejected the null hypothesis, you have evidence to support the alternative hypothesis. If you failed to reject the null hypothesis, there isn’t enough evidence to support the claim.

Preparing for Probability-Based Questions

In assessments that involve numerical analysis, problems based on chance and likelihood are common. These challenges require you to calculate the probability of different outcomes and apply fundamental principles to determine the likelihood of specific events occurring. To solve these types of problems efficiently, a solid understanding of probability rules and methods is essential.

Here are some key strategies to prepare for problems involving probability:

• Understand Key Probability Concepts: Familiarize yourself with fundamental terms like sample space, events, independent vs. dependent events, and mutually exclusive events.
• Learn the Different Probability Rules: Be comfortable with the addition and multiplication rules. Knowing when to apply these rules can significantly simplify complex scenarios.
• Practice with Common Probability Distributions: Study binomial, normal, and Poisson distributions, as these are frequently tested in probability problems.

Additionally, mastering the following methods will help you solve problems more effectively:

1. Counting Techniques: Be able to calculate combinations and permutations. These methods are essential when determining the number of possible outcomes in a given situation.
2. Conditional Probability: Understand how to calculate the probability of an event occurring given that another event has already occurred. Practice solving problems that involve conditional scenarios.
3. Bayes’ Theorem: Familiarize yourself with this important formula, especially when dealing with complex problems that require updating probabilities based on new information.

With consistent practice and a strong grasp of these concepts, you will be well-prepared to handle any problem involving likelihood and probability.

Data Interpretation Tips for Exam Success

Interpreting numerical data accurately is a crucial skill for solving many types of problems. Whether you are working with charts, tables, or graphs, being able to extract the right information and draw conclusions from it will greatly enhance your ability to succeed in any assessment. Developing a systematic approach to reading and analyzing data can help you make better decisions and avoid common mistakes.

Here are some essential tips for interpreting data effectively:

• Read the Question Carefully: Always start by understanding what the question is asking. Identify the key pieces of information that will guide your interpretation of the data.
• Analyze the Data Type: Recognize the type of data you’re working with–whether it’s categorical, numerical, or ordinal–so you can choose the correct method for analysis.
• Pay Attention to Units: Always double-check the units used in the data (e.g., percentages, counts, time) to ensure you are interpreting the values correctly.

Understanding the structure of data tables and graphs is also essential. Here’s a breakdown of some common visual representations:

Type of Data Representation	Key Points to Focus On	Common Errors to Avoid
Bar Graph	Look at the height of each bar and compare categories.	Confusing the scale or misinterpreting the data categories.
Pie Chart	Focus on the proportions represented by each segment.	Misjudging the size of the segments or missing small segments.
Line Graph	Analyze trends and changes over time.	Overlooking outliers or failing to interpret trends correctly.

By developing a keen eye for these details, you will be better prepared to interpret data quickly and accurately, ultimately improving your performance in any analysis-based problem.

Common Mistakes in Statistics Exams

When working through numerical problems, it’s easy to make mistakes that can affect the outcome of your analysis. These errors can range from simple miscalculations to more complex misunderstandings of concepts. Being aware of the most common mistakes can help you avoid them and improve your performance during an assessment. In this section, we will discuss some of the frequent pitfalls students encounter and how to steer clear of them.

Calculation Errors

One of the most frequent mistakes is making errors during mathematical calculations. Whether it’s incorrectly adding, subtracting, multiplying, or dividing, even small mistakes can lead to incorrect answers. It’s crucial to double-check your work and ensure each step is completed correctly.

Misinterpreting Data

Another common error is misunderstanding the data presented in tables, graphs, or problem statements. Failing to properly read values or misinterpreting units can lead to inaccurate conclusions. Always pay close attention to the specifics of the data provided and verify each detail before proceeding with your solution.

Type of Mistake	Common Causes	How to Avoid
Calculation Errors	Rushing through steps, overlooking signs or decimal points	Double-check each calculation, especially when working with complex numbers
Misinterpreting Data	Not recognizing units, failing to understand what data represents	Carefully review data before making assumptions or drawing conclusions
Wrong Test Selection	Choosing an incorrect method for the problem type	Familiarize yourself with different test methods and when to apply them

By staying aware of these common mistakes and developing strategies to avoid them, you can significantly improve your accuracy and efficiency during assessments.

Essential Formulas You Need to Know

When tackling mathematical problems, having a strong grasp of key formulas is essential for solving challenges efficiently. Formulas serve as tools that simplify complex calculations and help you derive solutions faster. In this section, we’ll cover some of the most important equations and principles you need to be familiar with to perform well in any assessment involving numerical data.

Fundamental Equations

These core formulas are essential for handling basic calculations, and they often serve as the foundation for more advanced problems:

• Mean (Average): (Σx) / n – The sum of all data points divided by the number of data points.
• Variance: σ² = (Σ(x – μ)²) / n – Measures the spread of data points around the mean.
• Standard Deviation: σ = √variance – Represents the average deviation from the mean.

Probability and Distribution Formulas

Probability calculations are central to many data analysis problems. Understanding the relevant formulas will help you solve these problems accurately:

• Binomial Probability: P(X = k) = (nCk) * p^k * (1-p)^(n-k) – Used to calculate the probability of k successes in n trials.
• Normal Distribution Z-Score: Z = (X – μ) / σ – Standardizes a data point within a normal distribution to find its probability.
• Conditional Probability: P(A|B) = P(A ∩ B) / P(B) – The probability of event A occurring given that B has occurred.

By memorizing and understanding how to use these formulas, you’ll be equipped to tackle a wide range of problems effectively and efficiently.

Time Management During the Exam

Effective time management is crucial when faced with a series of problems under a time constraint. Balancing the available time between reading, analyzing, and solving each challenge requires strategic planning. Developing a clear approach to allocating time ensures you can tackle all the tasks and avoid feeling rushed as the clock ticks down. By following a structured plan, you can maximize your efficiency and performance.

Here are some strategies to help you manage your time during an assessment:

• Plan Your Time: Before you begin, quickly scan the entire set of tasks to get an idea of the complexity and how long each one may take.
• Allocate Time for Each Section: Based on the number of questions or tasks, assign a time limit to each one. Stick to these limits to avoid spending too much time on any single task.
• Prioritize Easy Tasks: Start with questions you feel most confident about. This ensures that you secure those points and build momentum for the more difficult problems.

Here’s a breakdown of how you might allocate your time for different sections in a typical test:

Task Type	Suggested Time Allocation	Notes
Short Answer	10-15 minutes	These usually require quick calculations or short responses. Finish them first to gain confidence.
Multiple Choice	20-25 minutes	Read the questions carefully, but don’t overthink. Eliminate obviously incorrect options quickly.
Long Answer	30-40 minutes	Reserve enough time to fully explain your solution. Break down each part of the question for clarity.

By maintaining a steady pace and following these time management strategies, you will be able to complete all tasks within the allotted time and maximize your performance.

Strategies for Multiple-Choice Questions

Multiple-choice tasks often test your ability to quickly identify the correct answer from a set of options. While these tasks may seem straightforward, having a strategy for approaching them can greatly improve your accuracy and efficiency. By using the right techniques, you can eliminate incorrect choices and confidently select the best possible response.

Effective Approaches

Here are some strategies to use when tackling multiple-choice tasks:

• Read the Question Thoroughly: Ensure you understand exactly what is being asked before looking at the choices. Misunderstanding the prompt can lead you to choose the wrong option.
• Eliminate Obvious Incorrect Options: If you can quickly identify one or two wrong answers, cross them off. This will increase your chances of selecting the correct choice from the remaining options.
• Look for Keywords: Pay attention to qualifying words like “always”, “never”, “all”, and “some”. These words can help you identify correct or incorrect responses more easily.

Advanced Tips for Success

For more challenging tasks, consider these additional tips to improve your chances:

• Use Logic to Narrow Down Choices: Sometimes, even if you’re unsure, you can logically deduce the most likely answer based on what you know about the subject matter.
• Don’t Overthink: If you have a gut feeling about an answer, trust it. Often, your first instinct is the correct one. Avoid second-guessing yourself unless you’re sure you’ve made a mistake.
• Look for Patterns: In some cases, answers with similar wording or structure might indicate the correct option. Be on the lookout for consistent patterns across the answer choices.

By applying these strategies, you’ll be able to approach multiple-choice tasks more effectively and increase your likelihood of selecting the right answer.

Tips for Calculating Confidence Intervals

Calculating confidence intervals is an essential skill for estimating a range of values within which the true parameter is likely to fall. Whether you’re working with population means, proportions, or other metrics, understanding how to properly compute these intervals helps provide more accurate and reliable results. In this section, we will discuss some key tips to make the process of calculating confidence intervals more efficient and accurate.

• Know the Formula: The basic formula for a confidence interval is CI = Sample Mean ± (Critical Value * Standard Error). It’s important to understand each part of the formula and how they are calculated.
• Choose the Correct Critical Value: The critical value depends on the level of confidence you want to achieve (typically 90%, 95%, or 99%). These values are derived from standard distributions like the Z-distribution or t-distribution, depending on your sample size and whether the population standard deviation is known.
• Calculate the Standard Error: Standard error is the standard deviation of the sample mean, calculated as SE = σ / √n. Ensure you’re using the correct standard deviation (population vs sample) based on the context.

Remember, the wider the interval, the greater the confidence that the true parameter is within the interval, but it also means less precision. Striking a balance between accuracy and confidence is key.

How to Tackle Regression Analysis Problems

When facing regression analysis tasks, the goal is to understand the relationship between variables and use that insight for predictions or inferences. These problems often require careful interpretation of data, model fitting, and evaluation of the results. By following a structured approach, you can tackle regression tasks with confidence and precision.

• Understand the Variables: Before diving into calculations, familiarize yourself with the variables involved. Identify the dependent and independent variables and ensure you understand their roles in the analysis.
• Choose the Right Model: There are various types of regression models, such as linear and multiple regression. Based on the complexity of your data, select the model that fits the situation.
• Check Assumptions: Regression models often come with assumptions like linearity, independence, and homoscedasticity. Ensure these assumptions are met before proceeding with the analysis.

Once you’ve selected the appropriate model, proceed with the following steps to complete the analysis:

1. Fit the Model: Use available data to estimate the coefficients and fit the regression model. This process involves determining how each independent variable influences the dependent variable.
2. Evaluate the Results: After fitting the model, evaluate the goodness of fit using metrics such as R-squared, p-values, and residual plots. These will help you assess how well the model explains the data.
3. Make Predictions: With a well-fitted model, you can now use it to make predictions about new data points. Ensure that your predictions are within a reasonable range and consider the confidence intervals of your estimates.

By following these steps, you can effectively tackle regression analysis problems and make informed conclusions based on your data.

Real-World Applications of Statistics

The power of analyzing data goes beyond the classroom, influencing a wide range of industries and decision-making processes. Whether in business, healthcare, technology, or social sciences, data analysis plays a pivotal role in shaping strategies, improving outcomes, and guiding choices. Understanding how data can be applied in real-world situations enhances both the relevance and the impact of mathematical methods.

• Healthcare: Medical researchers use data to evaluate the effectiveness of treatments, predict disease outbreaks, and identify risk factors. Patient outcomes, treatment efficacy, and the development of new drugs all rely on rigorous analysis of data.
• Business and Marketing: Companies use data analysis to understand customer behavior, forecast demand, and optimize inventory. By studying patterns and trends, businesses can refine their marketing strategies and increase profitability.
• Sports Analytics: In sports, data is used to assess player performance, predict outcomes, and improve team strategies. From analyzing player statistics to using advanced metrics for team selection, data is a key factor in the modern sports industry.
• Environmental Science: Scientists analyze environmental data to track climate change, predict weather patterns, and manage natural resources. Accurate modeling helps in making informed decisions about conservation and sustainability.

Through these examples, it’s clear that data analysis is integral to various fields. It enables professionals to make informed decisions, predict future trends, and implement effective solutions in the real world.

How to Review Practice Problems Effectively

Reviewing practice tasks is a crucial step in reinforcing your understanding of key concepts. Simply solving problems is not enough; a thoughtful approach to revisiting and analyzing your solutions ensures long-term retention and improves your problem-solving skills. By reflecting on your mistakes and understanding the reasoning behind correct answers, you can maximize your preparation and increase your chances of success.

• Understand the Concept: Before reviewing a problem, ensure you fully grasp the underlying principles. Understanding the theory behind each task helps you apply the correct methods and techniques in similar future challenges.
• Identify Mistakes: Focus on any errors you made and determine why they happened. Were there gaps in your knowledge? Did you misinterpret the question? Identifying the root cause of mistakes can guide your future study sessions.
• Practice Similar Problems: After reviewing the mistake, find similar problems to work through. Repetition helps solidify your understanding and boosts your confidence in applying the learned concepts.

When reviewing, make sure to take your time and approach the process systematically:

1. Break Down the Solution: Go step-by-step through the solution, understanding how each part contributes to the overall answer. This will reinforce your understanding of the process.
2. Ask Why: Always ask yourself why a particular solution works and why other choices are incorrect. This deeper level of questioning enhances comprehension and reduces the chance of repeating the same errors.
3. Utilize Resources: Don’t hesitate to refer back to textbooks, notes, or online resources if something isn’t clear. Additional explanations can provide new insights into difficult concepts.

By effectively reviewing your practice tasks, you improve your problem-solving skills and develop a deeper understanding, allowing you to confidently tackle even more complex challenges.

What to Expect in Your Statistics Exam

As you approach your assessment, it’s important to understand what to expect and how to best prepare for the challenges that lie ahead. The tasks will test your ability to apply key concepts, solve complex problems, and demonstrate your understanding of various methods. Being familiar with the structure and types of tasks you will encounter helps reduce anxiety and boosts your confidence.

Generally, the assessment will focus on a range of topics, including data analysis, probability, hypothesis testing, and interpretation of results. You will be asked to analyze given data sets, make inferences, and apply appropriate techniques to draw conclusions. You may encounter both theoretical questions, which test your understanding of concepts, and practical problems, which assess your ability to perform calculations and interpret outcomes.

Additionally, you can expect tasks that require you to:

• Identify Key Relationships: You may need to recognize patterns or correlations in data and determine which methods to apply for analysis.
• Use Formulas: Be prepared to use essential formulas for calculating values such as means, variances, or confidence intervals.
• Interpret Graphs and Tables: Tasks might include interpreting visual data representations and extracting meaningful insights from them.

Knowing the structure and types of challenges you will face helps you focus your study efforts on the areas that matter most. By practicing these techniques and understanding the content thoroughly, you’ll be ready to tackle the assessment with confidence.