Go Math Lesson 6.1 Answers and Solutions

Mastering the core principles of problem-solving is essential for students who want to develop strong reasoning abilities. In this section, we will explore various methods to approach complex tasks, focusing on building a solid foundation for future challenges. By breaking down each problem into manageable steps, you will be able to grasp the concepts more clearly and apply them effectively in different situations.

Clear explanations and step-by-step guidance are key to navigating through problems confidently. Whether you’re solving abstract questions or tackling practical scenarios, the strategies discussed here will help you understand the underlying concepts. This approach not only aids in solving the current exercises but also prepares you for more advanced topics.

Through consistent practice and focused effort, you will enhance your problem-solving skills and gain a deeper understanding of key principles that extend beyond the classroom. The techniques provided here aim to make complex concepts accessible and engaging, ensuring a smooth learning experience.

Go Math Lesson 6.1 Answers Overview

In this section, we will provide a comprehensive breakdown of the key solutions and techniques used to solve various problems. The goal is to help students build a deeper understanding of the methods required to approach similar tasks in the future. By analyzing the structure of each solution, you will gain insight into how to apply these strategies to a wide range of challenges.

Understanding the Core Concepts

Every problem is built on a foundation of essential principles. By reviewing the solutions step by step, you can recognize the patterns and techniques that are commonly used to reach accurate results. With a clear grasp of these fundamentals, tackling more complex questions becomes much easier.

Improving Problem-Solving Skills

Success in solving tasks relies heavily on developing strong problem-solving abilities. By applying the correct strategies and methods, students can approach exercises with confidence. Practice is key to mastering these techniques, as it reinforces the understanding and ensures long-term retention of the material.

Key Concepts in Lesson 6.1

In this section, we will explore the fundamental ideas that form the backbone of the exercises. Understanding these core principles is crucial for successfully tackling the related problems. By recognizing the patterns and connections between various concepts, students can develop a strong grasp of the material and apply it effectively in different contexts.

Breaking Down the Problem-Solving Process

Each task involves specific steps that must be followed in a logical order. These steps not only help in arriving at the correct solution but also in building a structured approach to tackling future challenges. Grasping the sequence of actions and the relationships between elements is essential for mastering the topic.

Key Techniques for Effective Solutions

By using specific strategies, such as breaking down complex questions into smaller, more manageable parts, students can simplify the process. Focus on understanding the underlying techniques, as they provide a solid foundation for solving a wide range of problems. Mastering these techniques ensures accuracy and efficiency in solving future tasks.

Step-by-Step Solutions for Problems

In this section, we will break down complex problems into smaller, more manageable steps. Each solution is designed to guide you through the process methodically, ensuring a clear understanding of how to approach similar tasks in the future. By following these steps, you will gain confidence and improve your problem-solving skills.

Understanding the Process

To tackle each problem effectively, it is essential to understand the key steps involved. Here’s a general approach:

1. Identify the question: Carefully read the problem to understand what is being asked.
2. Choose a strategy: Select the appropriate method or approach to solve the problem.
3. Execute the plan: Apply the chosen strategy, breaking down the problem into simpler tasks.
4. Review the solution: Double-check the steps to ensure accuracy and correctness.

Tips for Effective Problem Solving

While solving problems, consider these helpful techniques:

• Start with simple examples: Practice with easier problems to build confidence before tackling more complex ones.
• Work step by step: Break down each problem into smaller pieces to avoid feeling overwhelmed.
• Stay organized: Keep track of your work to avoid mistakes and ensure logical progression.
• Check your work: Always review your solution to confirm accuracy.

Understanding Go Math Methods

In this section, we will explore the techniques and strategies that form the foundation of solving various exercises. These methods are designed to help students approach problems in a structured way, providing clarity and efficiency. By understanding these techniques, students can enhance their ability to solve problems more effectively and confidently.

Breaking Down the Approach

Each problem requires a methodical approach to ensure the most accurate solution. By identifying the right strategy and applying it consistently, students can tackle tasks with precision. The core idea is to simplify complex questions into manageable steps, making the process easier to follow and execute.

Key Strategies for Success

Successful problem-solving relies on mastering certain techniques. Some of these include:

• Visualization: Drawing diagrams or charts can help in understanding relationships between elements in a problem.
• Step-by-step analysis: Breaking down the task into smaller parts allows for a more organized approach.
• Pattern recognition: Identifying recurring patterns can speed up the solving process and ensure greater accuracy.

Common Mistakes in Lesson 6.1

As students work through exercises, certain errors tend to occur frequently. Understanding these common mistakes is essential for improving accuracy and avoiding setbacks. By identifying and addressing these pitfalls, learners can develop a clearer approach and strengthen their overall problem-solving abilities.

One frequent mistake is overlooking key details in the problem statement. Misinterpreting the question or missing important information can lead to incorrect conclusions. Additionally, rushing through calculations without double-checking steps often results in minor errors that affect the final answer.

Another common issue is misunderstanding the process behind applying certain techniques. Skipping essential steps or applying strategies incorrectly can derail the solution. It’s important to stay focused on following the prescribed method carefully and checking each step along the way to ensure accuracy.

Practice Exercises for Mastery

To truly master any skill, consistent practice is key. This section will focus on exercises that help reinforce the concepts covered, ensuring a deeper understanding and better retention of the material. By regularly engaging with these tasks, students can solidify their knowledge and approach future problems with greater confidence.

Recommended Practice Strategies

For effective practice, it’s important to follow a structured approach. The following strategies can help enhance learning:

• Start with simple exercises: Begin with easier problems to build confidence before progressing to more challenging tasks.
• Gradually increase difficulty: As your skills improve, tackle more complex problems to deepen your understanding.
• Track your progress: Keep a record of the exercises completed and review your solutions to identify areas for improvement.

Types of Practice Problems

To ensure comprehensive learning, it’s important to engage with different types of exercises:

1. Basic skill reinforcement: These problems focus on fundamental techniques and principles.
2. Application exercises: These tasks challenge you to apply concepts to real-world scenarios.
3. Critical thinking problems: These exercises encourage deeper analysis and reasoning to solve more complex questions.

Visual Aids and Diagrams for Clarity

Visual aids, such as diagrams, charts, and illustrations, are invaluable tools for enhancing understanding and simplifying complex problems. These tools help to break down abstract concepts into more tangible, easy-to-understand visuals. By incorporating these visual elements, students can gain a clearer view of the relationships between different components of a problem and improve their ability to solve it effectively.

Benefits of Using Visual Aids

Incorporating visual elements into the problem-solving process offers several advantages:

• Improved comprehension: Diagrams can make abstract ideas more concrete, helping to better grasp the material.
• Enhanced retention: Visuals often make information easier to remember, aiding in long-term recall.
• Faster problem-solving: A well-drawn chart or graph can quickly clarify relationships between data points, speeding up the solution process.

Types of Visual Aids to Use

There are several types of visuals that can be used to enhance learning:

1. Graphs: These are useful for representing numerical relationships and trends.
2. Flowcharts: Flowcharts can show step-by-step processes, helping students understand the sequence of actions needed to solve a problem.
3. Diagrams: Diagrams are ideal for illustrating spatial relationships and structures, such as geometric figures or networks.
4. Tables: Tables organize data in a clear, structured format, making it easier to analyze and compare information.

How to Approach Word Problems

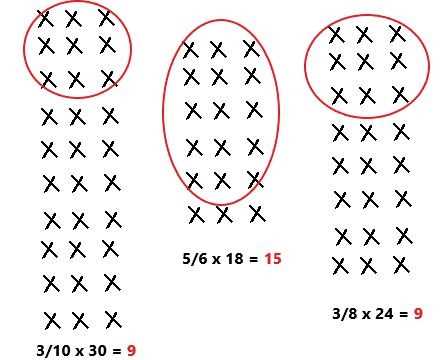
Word problems can often seem overwhelming, but with the right approach, they become more manageable. The key to solving these types of problems lies in understanding the situation described and translating it into a format that can be worked with. By following a systematic method, you can break down the problem into smaller, more solvable parts.

Step-by-Step Strategy

To effectively solve word problems, consider using the following steps:

• Read the problem carefully: Make sure to understand all details, identifying important information and key numbers.
• Identify the question: Focus on what the problem is asking. Highlight or underline the main objective.
• Plan a solution: Choose the appropriate strategy or method based on the information provided.
• Work through the steps: Apply the chosen method, breaking the problem down into smaller steps to simplify the process.
• Review and check: Once the solution is reached, revisit the problem to ensure accuracy and consistency with the question.

Common Strategies for Word Problems

There are several strategies that can be applied to word problems to improve efficiency and clarity:

• Draw a diagram or chart: Visual representations can often clarify the relationships between different parts of the problem.
• Set up equations: Translating word problems into mathematical expressions can make them easier to handle.
• Work backwards: Sometimes solving from the desired outcome can help you identify the necessary steps.

Tips for Quick Problem Solving

Effective problem-solving requires both speed and accuracy. To solve problems quickly, it’s important to develop a strategy that allows you to approach each task efficiently. By mastering certain techniques and honing your skills, you can improve your ability to tackle challenges rapidly and confidently.

One way to enhance your speed is by breaking down complex problems into smaller, more manageable steps. Additionally, being familiar with key methods and practicing them regularly can help reduce the time spent on each task.

Tip	Description
Understand the problem first	Take a moment to fully grasp the situation before jumping into the solution. This prevents mistakes that can slow you down later.
Use shortcuts	When possible, apply shortcuts or previously learned techniques that simplify calculations or steps.
Stay organized	Write down each step clearly to avoid confusion and ensure that you follow a logical path.
Eliminate unnecessary steps	Avoid overcomplicating the process. Focus on what is truly necessary to reach the solution.
Practice regularly	The more problems you solve, the quicker you will get at recognizing patterns and applying the best strategies.

Real-World Applications of Math

Understanding how abstract concepts are applied in everyday life helps to bridge the gap between theory and practice. The principles covered in various lessons have far-reaching implications, extending into numerous fields and influencing the way we solve problems, make decisions, and interact with the world. From financial planning to architecture, the skills developed through mathematical thinking have practical uses that impact daily living.

These concepts are not just confined to classrooms or textbooks; they are used by professionals and individuals alike to solve real-world challenges. Whether you are analyzing data, optimizing processes, or planning a project, the skills acquired from learning these principles are invaluable in making informed decisions and improving efficiency.

Concepts Explained in Simple Terms

Understanding complex ideas can be challenging, but breaking them down into simpler terms makes them easier to grasp. The key to mastering difficult topics is not to overwhelm yourself with jargon, but rather to focus on the basic principles. By relating concepts to real-life examples and using clear explanations, these ideas can become more accessible and intuitive.

Key Ideas to Keep in Mind

• Focus on the fundamentals: Understanding the core principles helps you build a solid foundation for tackling more complex problems later.
• Use simple examples: Start with small, easy-to-understand examples that illustrate the concept before diving into more complicated scenarios.
• Break it down step-by-step: Divide the process into smaller, manageable parts to avoid feeling overwhelmed.

Relating Concepts to Everyday Life

One effective method for understanding new ideas is to relate them to real-world situations:

1. Budgeting: Learning to manage money involves basic concepts like addition, subtraction, and multiplication. These principles are the same as those used in solving problems related to finances.
2. Building projects: Constructing anything, whether a house or a simple DIY project, requires understanding measurements, proportions, and space, all of which are based on fundamental principles.
3. Cooking: Following a recipe often involves measurements and ratios, which are concepts rooted in basic arithmetic and proportion.

Review of Essential Skills

Mastering fundamental skills is crucial for tackling more advanced tasks and solving problems effectively. A solid grasp of key concepts allows you to approach challenges with confidence and clarity. By revisiting core techniques, you can reinforce your understanding and identify areas that may need more focus. This review will highlight the essential skills necessary for building a strong foundation in various problem-solving contexts.

Core Skills to Review

Before moving forward, it’s helpful to review the following skills:

• Operations with numbers: Knowing how to add, subtract, multiply, and divide quickly and accurately is foundational for any problem-solving process.
• Understanding patterns: Recognizing trends or repeating sequences can help in predicting outcomes and solving complex problems with greater ease.
• Logical reasoning: Being able to think critically and follow a step-by-step process ensures that you can solve problems efficiently without skipping essential steps.

Applying Skills to Solve Problems

Reinforcing these skills will allow you to approach new problems with a clear strategy. Whether you’re calculating, analyzing data, or simply breaking down a task, applying these core skills consistently will make complex challenges more manageable.

Additional Resources for Practice

To deepen your understanding and gain more hands-on experience, it’s important to explore various resources beyond the classroom. These materials can provide additional exercises, examples, and explanations to help reinforce what you’ve already learned. Whether you’re looking for interactive tools, worksheets, or video tutorials, there are numerous ways to practice and enhance your skills.

Online Platforms and Tools

Many websites offer free exercises and tutorials that cater to various learning styles:

• Interactive quizzes: Websites like Khan Academy and IXL provide practice quizzes with instant feedback to track progress and identify areas for improvement.
• Video tutorials: YouTube channels such as CrashCourse and PatrickJMT explain difficult concepts in simple, visual ways, helping you understand topics at your own pace.
• Problem-solving apps: Mobile apps like Photomath and WolframAlpha can be used to solve problems step-by-step, offering detailed explanations and solutions.

Books and Worksheets

For those who prefer offline study materials, consider the following resources:

• Practice workbooks: Many publishers offer workbooks specifically designed for reinforcing key skills, providing practice problems with solutions.
• Study guides: Comprehensive study guides offer summaries of important topics and additional practice problems for in-depth learning.
• Workbooks for specific topics: Focusing on specific areas can help strengthen any weak points, providing targeted exercises to master individual concepts.

How to Check Your Answers

Reviewing your work is an essential step in ensuring accuracy and understanding. By verifying your results, you can identify mistakes, clarify your thought process, and confirm that you have followed the correct steps. Checking your solutions systematically helps to build confidence and improves overall problem-solving skills.

Here are a few methods to effectively check your results:

• Revisit the problem: Read the problem again to ensure that you understood the question correctly. Make sure you’re addressing the correct concepts and operations.
• Use a different approach: If possible, solve the problem using a different method to see if you arrive at the same result. This can help confirm the correctness of your solution.
• Estimate your answer: Before performing detailed calculations, estimate what a reasonable answer might be. Comparing the actual result to your estimate can highlight any obvious errors.
• Check each step: Break down your process step-by-step to verify that each calculation or decision was done correctly. This helps catch small mistakes that might have been overlooked.
• Cross-check with resources: If available, use a calculator, online tool, or reference materials to verify your solution. This provides additional confirmation of the accuracy of your results.

Exploring Different Problem Types

Understanding various problem types is crucial for developing strong problem-solving skills. Each type challenges you in different ways, requiring unique approaches and techniques. By familiarizing yourself with different problem categories, you can better prepare for tackling diverse situations with confidence and accuracy.

Here are some common problem types and tips on how to approach them:

• Word Problems: These problems present a scenario or story, and you must extract the relevant information to solve the issue. Focus on identifying key facts, operations, and the final goal. Breaking down the text into smaller parts often helps in finding the solution.
• Equations: Problems that involve solving for an unknown value require applying algebraic principles. Remember to simplify each side step by step, and check your work by substituting the solution back into the original equation.
• Graphing Problems: These tasks involve plotting points or interpreting data from graphs. Make sure to understand the axes, labels, and scales. Pay attention to the context of the graph for a more accurate interpretation of the data.
• Comparison Problems: These ask you to compare two or more sets of data, values, or conditions. Often, they involve determining relationships or differences between elements. Pay careful attention to the details and the specific aspects being compared.
• Optimization Problems: These require finding the best possible solution under given constraints. These problems often involve maximizing or minimizing certain values. Identify the limitations first, then explore different options to find the optimal solution.

Each of these problem types provides a unique challenge, but mastering the strategies for solving them will improve your overall problem-solving abilities. The key is practice and developing a systematic approach to each problem type you encounter.

How Go Math Builds Strong Foundations

Creating a solid foundation is crucial when tackling any complex subject. By gradually introducing core concepts and reinforcing them through consistent practice, students can develop a deep understanding that prepares them for future challenges. This structured approach allows learners to connect new information with previously learned material, making each step more manageable and meaningful.

Sequential Learning for Better Retention

The key to building a strong foundation lies in the methodical progression of topics. Each concept introduces essential skills that are further expanded upon, ensuring that foundational knowledge is solidified before moving on to more advanced topics. This type of learning approach helps in reducing confusion and enhancing long-term retention.

Active Engagement and Practice

Active participation is encouraged throughout the process. Students are not only exposed to new information but also given opportunities to apply it in various settings, reinforcing their understanding. Practice exercises and real-world examples keep learners engaged, promoting hands-on experience that leads to mastery of concepts.

Stage	Focus	Outcome
Introduction	Basic understanding and key concepts	Foundation for advanced skills
Development	Building on earlier concepts with practice	Stronger retention and comprehension
Application	Real-world problems and exercises	Mastery of concepts and practical use

This progression ensures that each student can build their knowledge base step by step, without feeling overwhelmed. The focus on understanding each layer thoroughly before advancing helps in solidifying essential skills and making learning a more rewarding experience.