Algebra 1 Semester 1 Exam Review Answers

When preparing for a crucial assessment in mathematics, understanding the foundational principles is key to achieving a strong performance. The journey involves revisiting essential topics and strengthening problem-solving skills. Whether you’re tackling linear equations, factoring expressions, or interpreting graphs, the ability to apply these concepts confidently is essential.
Structured preparation is often the best way to approach this challenge. By breaking down complex problems into manageable parts, you can systematically improve your skills and increase your chances of success. It’s important to focus on areas that require more attention and build on your strengths.
In this section, we will focus on key topics that are commonly tested, offering practical tips, strategies, and guidance to help you master the material. Each concept plays a vital role in ensuring you’re fully equipped to solve a wide range of problems quickly and accurately.
Algebra 1 Semester 1 Exam Review Answers
As you prepare for your upcoming test, it’s essential to consolidate your understanding of key mathematical concepts. By revisiting foundational topics, you can sharpen your skills and increase your ability to solve problems accurately. This section will help you focus on the most critical areas that are commonly tested, offering practical strategies and solutions.
Key Concepts to Master
- Linear equations and their solutions
- Graphing and interpreting functions
- Factoring expressions and solving quadratic equations
- Understanding systems of equations and their solutions
- Working with rational expressions and inequalities
Strategies for Success
- Review practice problems regularly to reinforce concepts.
- Work through sample questions to gain familiarity with question types.
- Focus on common mistakes and identify ways to avoid them.
- Ensure a strong understanding of basic operations to build confidence.
- Manage your time wisely during the test to avoid rushing.
By concentrating on these key areas and employing effective strategies, you’ll be well-prepared to tackle any questions that come your way during the assessment. Take the time to practice, and you’ll increase your chances of success. Good luck!
Key Concepts to Focus On
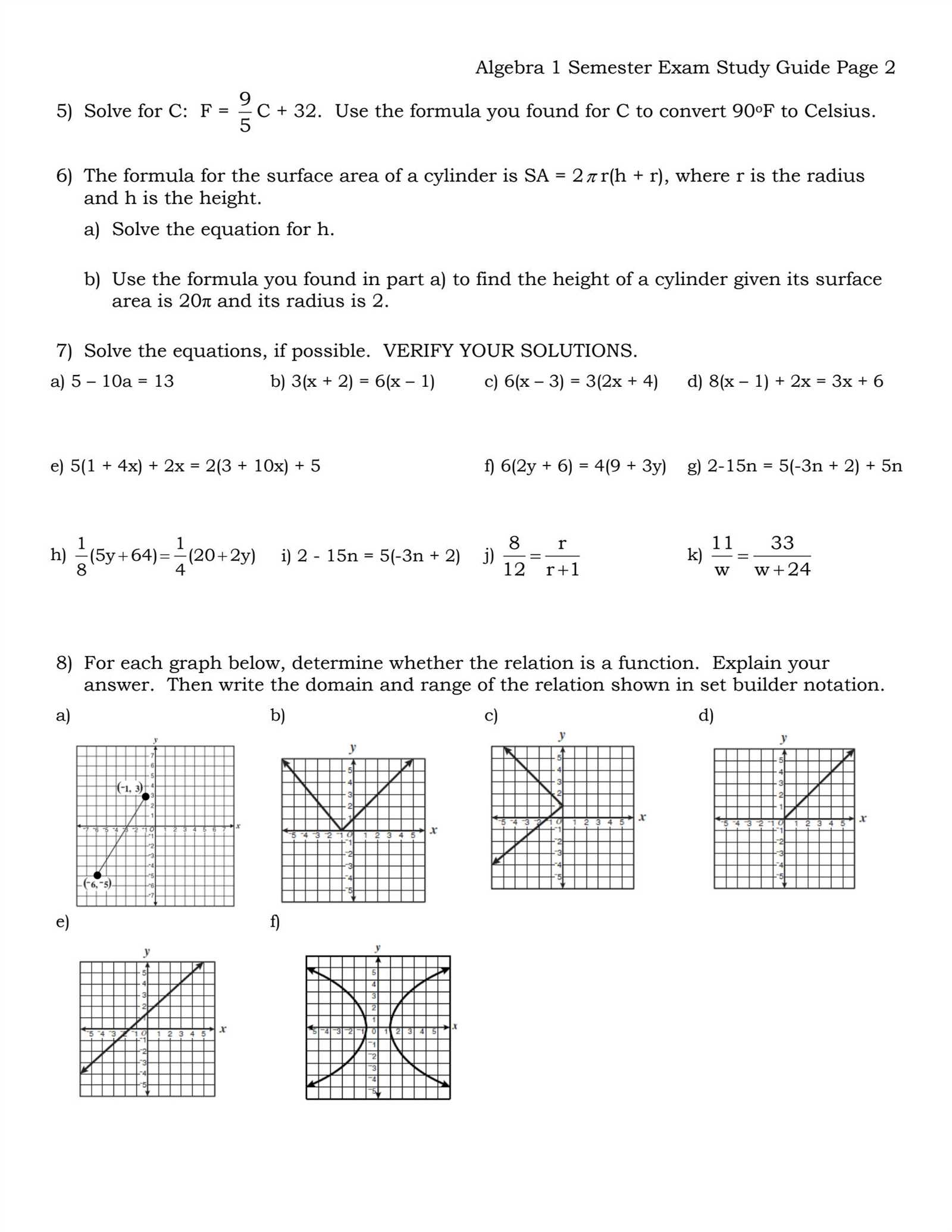
To excel in your upcoming assessment, it’s crucial to concentrate on the core mathematical principles that frequently appear in problems. A solid understanding of these topics will not only help you solve problems faster but also boost your confidence. In this section, we will highlight the most important concepts that you need to review and master for success.
Core Mathematical Areas

| Topic | Key Focus |
|---|---|
| Linear Equations | Solving for unknowns, graphing, understanding slope and intercepts |
| Functions and Graphing | Identifying functions, plotting graphs, and analyzing trends |
| Factoring Expressions | Breaking down expressions into simpler factors, solving quadratics |
| Systems of Equations | Solving simultaneous equations using various methods like substitution and elimination |
| Rational Expressions | Simplifying, multiplying, and dividing expressions involving fractions |
Essential Skills for Problem Solving
- Master the distributive property for simplifying expressions.
- Understand how to isolate variables in equations to find solutions.
- Get comfortable with graphing different types of functions and interpreting results.
- Practice solving word problems by translating them into mathematical expressions.
Focusing on these key areas will strengthen your foundation and help you approach problems with greater ease. Regular practice and a clear understanding of these concepts are essential to performing well.
Understanding Equations and Inequalities
Mastering equations and inequalities is a fundamental aspect of solving mathematical problems. These concepts involve relationships between variables that are governed by certain rules and operations. Whether you’re looking to find the value of a variable or analyze how different expressions compare, a strong grasp of these topics is crucial for success.
Equations represent statements of equality, where both sides are balanced. Solving these requires isolating the unknown variable through various mathematical operations. Inequalities, on the other hand, involve expressions where one side is greater than, less than, or not equal to the other. Understanding how to work with these relations is essential for solving a wide range of problems.
By practicing how to manipulate both equations and inequalities, you’ll develop the skills to approach more complex scenarios with confidence. Focus on solving simple equations first, then gradually move on to more advanced types, such as those with fractions or multiple variables. Similarly, mastering the rules for handling inequalities will help you recognize the correct solutions in different contexts.
Mastering Graphing Linear Functions
Graphing linear functions is a key skill that enables you to visualize relationships between variables. By plotting these functions on a coordinate plane, you can clearly understand how changes in one variable affect another. This process involves recognizing the form of the equation and using specific points to draw a straight line that represents the relationship.
Steps for Graphing Linear Functions
- Identify the slope and y-intercept from the equation.
- Plot the y-intercept on the graph (the point where the line crosses the y-axis).
- Use the slope to determine the rise over run and plot a second point.
- Draw a straight line through the two points, extending in both directions.
Key Concepts to Remember
- Slope represents the rate of change between the two variables.
- The y-intercept is the point where the line crosses the y-axis, showing the value when the other variable is zero.
- Positive slopes indicate an upward trend, while negative slopes indicate a downward trend.
By practicing these steps and concepts, you will become more efficient at graphing and interpreting linear functions. Understanding how to manipulate and plot these equations is essential for solving a wide range of problems in mathematics.
Factoring Techniques for Algebraic Expressions
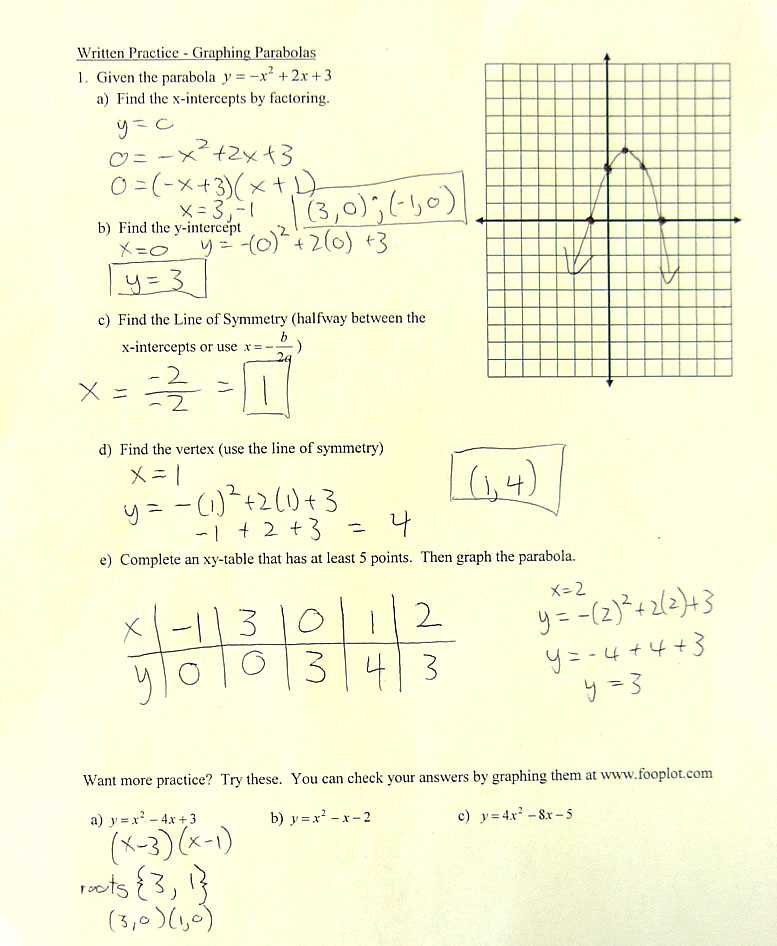
Factoring is a powerful tool used to simplify expressions and solve equations. By breaking down complex expressions into simpler factors, you can more easily solve problems involving polynomials. This process is essential for understanding how different terms in an expression relate to each other and can be rearranged to reveal solutions.
Common Factoring Methods
- Common Factor Extraction: Identify and pull out the greatest common factor (GCF) from all terms.
- Difference of Squares: Apply the formula a² – b² = (a – b)(a + b) to expressions that fit this pattern.
- Trinomial Factoring: Factor quadratic expressions into two binomials, such as ax² + bx + c.
- Grouping: Group terms in pairs to factor out common terms and then factor the resulting expression.
Helpful Tips for Effective Factoring
- Always look for the greatest common factor before trying other methods.
- In trinomials, try to find two numbers that multiply to give the constant term and add to the middle coefficient.
- Practice recognizing patterns, such as the difference of squares or perfect square trinomials, to factor more efficiently.
Mastering these factoring techniques will not only help you simplify expressions but also solve equations with greater ease. Regular practice is key to becoming proficient in identifying the right method for each problem.
Solving Systems of Equations
Solving a system of equations involves finding values for variables that satisfy all the given equations simultaneously. These problems require the use of different methods to determine the point or points where the equations intersect. Whether the system consists of linear or non-linear equations, mastering these techniques will allow you to find solutions efficiently.
Methods for Solving Systems
- Substitution Method: Solve one equation for one variable and substitute that expression into the other equation.
- Elimination Method: Add or subtract equations to eliminate one variable, making it easier to solve for the other.
- Graphing Method: Plot both equations on a graph and identify the point(s) where the lines intersect.
Example Problem
| Equation 1 | Equation 2 |
|---|---|
| x + y = 10 | 2x – y = 4 |
To solve this system, you can apply any of the methods mentioned above. For example, using substitution, you would solve the first equation for one variable (say, x = 10 – y) and substitute it into the second equation. Alternatively, the elimination method can be used to add the two equations to eliminate one of the variables.
By practicing different techniques, you’ll become more comfortable solving systems of equations and apply the most efficient method for each situation.
Polynomials and Their Properties
Polynomials are expressions made up of terms that are added or subtracted, with each term consisting of a variable raised to a power and multiplied by a coefficient. These expressions are central to solving many types of mathematical problems, and understanding their properties helps in simplifying, factoring, and solving equations. A good grasp of polynomials allows you to analyze how the terms interact and how changes in the coefficients or exponents affect the overall expression.
Key Properties of Polynomials
- Degree: The degree of a polynomial is determined by the highest exponent of the variable in the expression. It tells you the general behavior of the graph.
- Leading Coefficient: The leading coefficient is the coefficient of the term with the highest degree. It influences the direction of the graph for large values of the variable.
- Constant Term: The constant term is the value of the polynomial when all variables are set to zero. It represents the y-intercept of the graph.
- End Behavior: The end behavior describes how the polynomial behaves as the variable approaches infinity or negative infinity.
- Roots: The roots (or zeros) of a polynomial are the values of the variable that make the polynomial equal to zero. These are the x-intercepts of the graph.
Types of Polynomials
- Monomials: Polynomials with only one term.
- Binomials: Polynomials with two terms.
- Trinomials: Polynomials with three terms.
- Higher-Degree Polynomials: Polynomials with more than three terms, often requiring more complex methods to factor or solve.
Understanding these properties allows you to work with polynomials more effectively, whether you’re simplifying expressions, solving equations, or analyzing graphs. Mastering these concepts is essential for progressing to more advanced topics in mathematics.
Understanding Rational Expressions
Rational expressions are mathematical fractions that involve variables in both the numerator and denominator. Working with these expressions requires a solid understanding of how to simplify, multiply, divide, add, and subtract them. These operations are essential in solving complex equations and real-world problems where quantities are expressed as ratios.
Key Concepts of Rational Expressions
- Simplifying: To simplify a rational expression, factor both the numerator and denominator and cancel out any common factors.
- Restrictions: The denominator cannot be zero. Identifying and excluding values that make the denominator zero is crucial to avoid undefined expressions.
- Multiplication and Division: Multiply the numerators and denominators directly. For division, multiply by the reciprocal of the second fraction.
- Addition and Subtraction: To add or subtract rational expressions, find a common denominator, then combine the numerators accordingly.
Common Mistakes to Avoid
- Ignoring Restrictions: Always check for values that make the denominator zero before solving.
- Incorrect Factoring: Incorrectly factoring the numerator or denominator can lead to incorrect simplifications.
- Misapplying Operations: Be careful when applying operations like addition or subtraction; ensure that the denominators are properly factored or unified before proceeding.
Mastering rational expressions is essential for simplifying complex mathematical problems and dealing with equations involving fractions. With practice, you will be able to manipulate these expressions with confidence and accuracy.
Exponents and Their Rules
Exponents are a shorthand way to express repeated multiplication of the same number. They are used in many areas of mathematics and are essential for working with large numbers, polynomial expressions, and solving equations. Understanding the rules governing exponents will allow you to simplify expressions and solve problems more efficiently.
Key Rules for Exponents
- Product Rule: When multiplying terms with the same base, add the exponents. For example, am × an = am+n.
- Quotient Rule: When dividing terms with the same base, subtract the exponents. For example, am ÷ an = am-n.
- Power Rule: When raising a power to another power, multiply the exponents. For example, (am)n = am×n.
- Zero Exponent Rule: Any non-zero number raised to the power of zero equals 1. For example, a0 = 1.
- Negative Exponent Rule: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, a-n = 1 / an.
Examples and Applications
- Multiplying Powers: 32 × 34 = 36
- Dividing Powers: 57 ÷ 53 = 54
- Raising a Power: (23)2 = 26
- Negative Exponent: 2-3 = 1 / 23 = 1 / 8
Understanding and applying these rules will help you simplify expressions, solve equations, and handle complex problems with confidence. With practice, exponents become a powerful tool in your mathematical toolkit.
Working with Radicals in Algebra
Radicals are expressions that involve roots, such as square roots, cube roots, and higher-order roots. They are commonly encountered in problems involving equations, simplifications, and geometry. Understanding how to simplify, manipulate, and combine radical expressions is crucial for solving more complex mathematical problems efficiently.
Key Operations with Radicals
- Simplifying Radicals: To simplify a radical expression, look for perfect squares (or higher powers) within the radicand. For example, √36 = 6.
- Adding and Subtracting Radicals: Radicals can only be added or subtracted if they have the same radicand (the expression under the root). For example, √8 + √8 = 2√8.
- Multiplying Radicals: When multiplying two radicals with the same index, multiply the radicands. For example, √5 × √3 = √15.
- Dividing Radicals: Divide the radicands when dividing like radicals. For example, √25 ÷ √5 = √5.
Rationalizing the Denominator
In many cases, you will need to rationalize the denominator when it contains a radical. This means multiplying both the numerator and denominator by a radical that will eliminate the root in the denominator.
| Expression | Rationalized Form |
|---|---|
| 1 / √3 | √3 / 3 |
| 5 / √2 | 5√2 / 2 |
Mastering these operations will enable you to simplify expressions and solve equations involving roots with ease. As with all mathematical techniques, practice is key to becoming proficient with radicals and their properties.
Quadratic Equations and Solutions
Quadratic equations are polynomial equations that involve the square of an unknown variable. These equations are fundamental in many areas of mathematics and have multiple methods for finding their solutions. Understanding how to solve them is essential for progressing in various mathematical topics.
Methods for Solving Quadratic Equations
- Factoring: If the equation can be factored into two binomials, the solutions are the values of the variable that make each factor equal to zero. For example, (x – 2)(x + 3) = 0 gives x = 2 or x = -3.
- Quadratic Formula: The quadratic formula can be used to find the solutions of any quadratic equation in the form ax² + bx + c = 0. The formula is x = (-b ± √(b² – 4ac)) / 2a.
- Completing the Square: This method involves rearranging the equation to form a perfect square trinomial on one side, allowing you to solve for the variable. It is particularly useful when factoring is difficult.
Discriminant and Its Significance
The discriminant, found within the quadratic formula as b² – 4ac, helps determine the nature of the solutions. Based on its value, you can determine if the equation has real or complex solutions:
- If the discriminant is positive: There are two distinct real solutions.
- If the discriminant is zero: There is exactly one real solution (a repeated root).
- If the discriminant is negative: The solutions are complex (no real solutions).
By mastering these methods, you can efficiently solve quadratic equations and understand the nature of their solutions, which are vital skills for solving higher-level problems.
Word Problems and Algebraic Solutions
Word problems are a key aspect of applying mathematical concepts to real-world situations. These problems require translating a narrative into mathematical expressions and equations to find a solution. Developing the skill to interpret and solve these types of problems is crucial for mastering problem-solving techniques.
Steps to Solve Word Problems
- Read the problem carefully: Understand all the given information and what is being asked. Pay attention to units, relationships, and conditions mentioned.
- Define the variable: Let the unknown quantity be represented by a variable. This could be anything from the number of items to the time it takes to complete a task.
- Translate into an equation: Express the relationships in the problem using mathematical symbols. This may involve forming an equation from the given facts.
- Solve the equation: Use appropriate methods to solve the equation for the variable, such as substitution, elimination, or simplification.
- Interpret the solution: Ensure the solution makes sense in the context of the problem. Check for any units or conditions that were part of the original question.
Common Types of Word Problems
- Motion Problems: These involve objects moving at different speeds, often requiring the use of distance, rate, and time formulas.
- Work Problems: These involve tasks completed by one or more individuals working together or separately, typically requiring the use of rates of work.
- Mixture Problems: These problems deal with combining two or more substances with different properties to create a mixture with specific characteristics.
- Age Problems: These problems involve relationships between ages of individuals at different times.
By carefully following the steps and practicing with different types of problems, you can improve your ability to solve word problems and apply mathematical reasoning in everyday situations.
Tips for Solving Multiple Choice Questions
Multiple choice questions can be challenging, but with the right strategies, they become easier to tackle. These questions test your ability to recognize the correct answer among several options, making it crucial to approach them methodically. The key is to not just rely on intuition but also apply specific techniques that maximize your chances of success.
Effective Strategies for Multiple Choice
- Read the question carefully: Ensure that you fully understand what is being asked. Look for keywords or phrases that indicate the focus of the question.
- Eliminate obviously wrong answers: Start by crossing out options that are clearly incorrect. This increases your chances when you have to make an educated guess.
- Look for clues in other questions: Sometimes, later questions can give hints about earlier ones, especially if they cover similar material or concepts.
- Don’t rush: Take your time to analyze each option. Sometimes, the answer that seems correct at first glance may not be upon closer inspection.
- Use the process of elimination: Even if you’re unsure, eliminating at least one or two incorrect answers gives you better odds for guessing correctly.
Common Pitfalls to Avoid
- Overthinking: Avoid second-guessing yourself. Often, your first choice is the correct one.
- Getting stuck on one question: If you don’t know the answer right away, move on and come back to it later. Spending too much time on one question can waste valuable time.
- Ignoring negative wording: Pay attention to questions with phrases like “Which of the following is NOT…” These can throw you off if you don’t read carefully.
By applying these techniques, you can approach multiple choice questions with more confidence and improve your overall performance. Practice and preparation are key to mastering this format and boosting your scores.
How to Use a Calculator Effectively
Using a calculator can significantly speed up your problem-solving process, but it’s important to understand how to use it efficiently. While calculators are powerful tools, relying on them without a solid understanding of the underlying concepts can lead to mistakes. Mastering the calculator’s functions, along with practicing the right techniques, can enhance your ability to tackle complex problems quickly and accurately.
Here are some key tips for using a calculator effectively:
- Understand the functions: Make sure you are familiar with the basic and advanced functions of your calculator. Knowing where to find operations like square roots, exponents, or parentheses can save you time when solving problems.
- Use memory functions: Many calculators have memory storage capabilities. Store intermediate results when solving multi-step problems to avoid errors and reduce the need for repetitive calculations.
- Check the mode: Ensure your calculator is set to the correct mode, such as degrees vs. radians for trigonometric functions. Mismatched settings can lead to incorrect answers.
- Double-check your input: A simple mistake when entering numbers or operators can throw off your entire calculation. Always verify your input before hitting “enter” or “=”.
- Practice with the calculator: The more you use your calculator, the more comfortable you’ll become with its layout and features. Regular practice helps reduce the likelihood of errors during timed assessments.
By following these tips, you can harness the full potential of your calculator, allowing you to solve problems more efficiently while avoiding common pitfalls. It’s a valuable tool when used correctly, complementing your mathematical skills and enhancing your performance.
Common Mistakes to Avoid During the Exam
When faced with a timed assessment, it’s easy to make simple errors that can cost valuable points. Even with thorough preparation, stress or rushing through problems can lead to avoidable mistakes. Understanding and being mindful of these common pitfalls can help ensure you perform at your best and avoid costly errors.
Here are some typical mistakes to watch out for:
Rushing Through Questions
One of the most common errors is hurrying through problems without fully reading the instructions or carefully solving each step. While time constraints can be stressful, it’s important to pace yourself and allocate enough time to answer each question thoroughly. Skimming over important details can lead to misinterpretation of the problem or careless mistakes.
Misunderstanding the Question
It’s easy to assume you understand a question and jump right into solving it. However, failing to fully analyze the question can lead to incorrect approaches. Make sure to take a moment to break down the problem, highlight key information, and determine what is being asked before proceeding with your solution.
- Overlooking Negative Signs: Negative numbers often trip students up. Be cautious when dealing with negative values, especially when multiplying or dividing.
- Forgetting to Simplify: After completing a calculation, don’t forget to simplify your answer if necessary. Leaving your result in a complicated form can result in lost points.
- Skipping Units: Ensure that you include units when applicable, especially in word problems. Not doing so can lead to incomplete or incorrect answers.
Avoiding these mistakes is essential for maximizing your performance. By staying calm, focused, and attentive to detail, you can navigate through each problem with confidence and accuracy.
Strategies for Time Management
Efficiently managing time during a challenging assessment is crucial for success. With a limited amount of time, it’s important to prioritize tasks, pace yourself, and ensure you’re making the best use of the available minutes. Implementing effective strategies can help you stay on track and avoid feeling overwhelmed.
Start with the Easiest Problems
One effective approach is to begin with the questions that you find the easiest or most straightforward. This helps build confidence early on and ensures you’re accumulating points right from the start. By answering simpler questions first, you also avoid wasting time on difficult ones that might take longer to solve.
Allocate Time for Each Section
Before you start, take a moment to assess the number of questions and estimate how much time you should spend on each. Divide the total available time by the number of sections or questions, and set mini-deadlines for each part. This way, you can keep track of how much time you have left, ensuring you don’t get stuck on a single question for too long.
- Use a Timer: Set an alarm or timer to keep track of how much time you’re spending on each section or question.
- Don’t Dwell on Difficult Questions: If you encounter a challenging question, move on and return to it later. This prevents you from losing valuable time.
- Leave Time for Review: Always reserve the last few minutes to double-check your work and make sure you didn’t miss anything.
By organizing your approach and managing your time wisely, you can complete the tasks with greater efficiency and accuracy, helping you achieve the best possible outcome.
Reviewing Past Exams for Better Understanding
Going through previously completed tests can provide valuable insights and help reinforce your understanding of key concepts. By analyzing your past performance, you can identify areas where you made mistakes or encountered challenges. This process not only helps you avoid repeating those errors but also deepens your comprehension of the material.
Identify Patterns in Mistakes

When reviewing past assessments, pay close attention to recurring mistakes. Whether they stem from misunderstandings of specific topics or simple calculation errors, recognizing these patterns can help you focus on areas that need improvement. Make a list of these common issues and prioritize them during your study sessions to ensure you’re addressing the most critical gaps in your knowledge.
Understand the Format and Question Types
Familiarity with the format and types of questions is an important aspect of preparing for future assessments. By reviewing past tests, you can become more comfortable with the structure and learn to anticipate the types of problems that may appear. Understanding the way questions are phrased can also help you approach them with greater confidence and efficiency.
- Rework Incorrect Problems: Take the time to solve problems that you got wrong previously. Doing so will help you identify where your understanding faltered and allow you to correct misconceptions.
- Ask for Clarification: If there’s something you didn’t understand the first time, don’t hesitate to ask a teacher or peer for clarification.
- Practice Similar Problems: Once you’ve reviewed the mistakes, practice similar problems to reinforce your skills and build confidence.
By actively engaging with past tests, you can refine your approach and improve your performance in future assessments. Understanding where you went wrong and strengthening your weak points will give you the tools needed to succeed.