Cpm Algebra 2 Answer Key and Solutions Guide
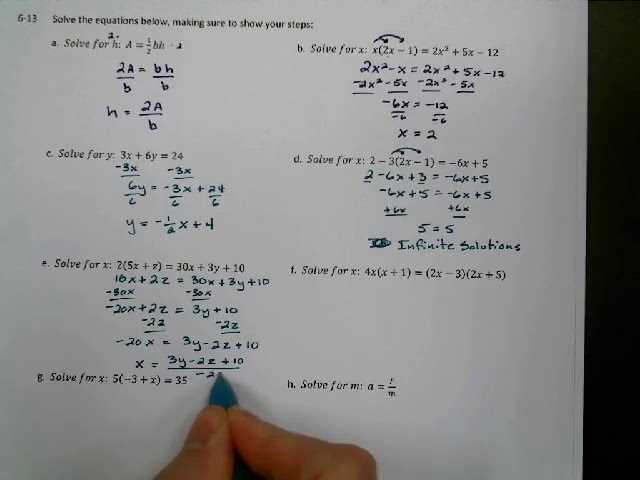
Mathematics often presents challenges that require a deeper understanding of concepts and problem-solving strategies. For students looking to enhance their skills, having access to reliable resources that break down difficult tasks can make all the difference. This section provides a comprehensive approach to tackling mathematical exercises with clarity and precision.
Understanding the process behind solving advanced equations is essential for anyone looking to improve their mathematical abilities. Step-by-step guides offer invaluable insights, allowing learners to grasp underlying principles and confidently apply them to various problems. Whether reviewing past material or preparing for future assessments, these resources provide crucial support.
By focusing on clear explanations and offering well-structured solutions, learners can not only check their work but also strengthen their problem-solving techniques. These materials are designed to assist both those struggling with specific topics and those seeking to fine-tune their skills in more complex areas of study.
Cpm Algebra 2 Answer Key Overview
This section explores the tools and resources that provide detailed solutions to complex mathematical problems. The focus is on materials designed to help learners navigate through various types of equations and tasks, offering insight into the correct methods and approaches. With these resources, students can better understand the process behind solving intricate problems and apply the knowledge more effectively in their studies.
Each solution set is carefully structured to guide learners through every step, highlighting important concepts and techniques. By breaking down problems into manageable steps, users can gain a deeper understanding of both basic and advanced topics, ultimately improving their ability to solve problems independently. These resources serve not only as a way to check the correctness of work but also as a tool for mastering challenging subjects.
How to Use the Cpm Algebra 2 Key
Effectively utilizing solution guides can significantly improve your understanding of complex mathematical concepts. These resources provide step-by-step explanations that help clarify difficult problems, ensuring that learners can follow along with ease. By using these solutions as a reference, students can check their work, identify mistakes, and learn the correct methods for tackling similar tasks.
Understanding the Structure of Solutions
The solutions are typically broken down into stages, making it easier to follow each step and comprehend the reasoning behind them. This structure allows learners to focus on one part of the problem at a time, reducing the chances of confusion. Additionally, many guides offer explanations for each mathematical operation, helping to solidify your grasp of the techniques involved.
Using Solutions for Practice and Review
These materials are not only for checking completed exercises but also for reinforcing concepts through practice. By working through problems independently first and then comparing your approach with the provided solutions, you can identify areas where further improvement is needed. This method of review ensures a deeper mastery of the subject and prepares you for more advanced topics.
Understanding Common Algebra 2 Problems
Many students encounter a variety of challenges when tackling more advanced mathematical exercises. By familiarizing yourself with the most common types of problems, you can develop effective strategies for solving them. These typical problems often involve intricate processes, and understanding the underlying concepts is key to approaching them confidently.
Types of Common Problems
Some of the most frequently encountered tasks involve the following areas:
- Solving linear and quadratic equations
- Working with polynomials and factoring
- Understanding systems of equations and inequalities
- Analyzing functions and their graphs
- Handling exponential and logarithmic expressions
Approaches to Solve These Problems
To effectively address these types of exercises, it’s helpful to follow a systematic approach:
- Identify the type of problem and choose the appropriate method
- Break the problem down into smaller, manageable steps
- Apply the correct formulas or operations for each step
- Check your work carefully and verify your solution
Mastering these common problems can significantly improve your problem-solving abilities and help you tackle more complex topics with ease.
Step-by-Step Solutions for Algebra 2
One of the most effective ways to master complex mathematical tasks is by breaking them down into manageable steps. Step-by-step solutions guide learners through each stage of a problem, making it easier to understand the logic behind every operation. This method not only ensures accuracy but also helps build confidence as students progress through challenging exercises.
Breaking Down the Problem
When tackling difficult problems, the first step is to identify the key components and determine the appropriate approach. Each solution starts with understanding the given information and choosing the right method to solve the equation or expression. By focusing on one part of the problem at a time, learners can avoid becoming overwhelmed.
Applying Mathematical Concepts
After breaking the problem into steps, it’s important to apply the correct formulas and principles to each stage. Whether it’s simplifying expressions, factoring, or solving for unknowns, using the right techniques ensures that each step logically follows the previous one. This structured approach helps students grasp how different concepts interconnect and reinforces their understanding of the material.
Why Cpm Algebra 2 Answers Are Helpful
Having access to solutions for complex mathematical problems can be incredibly valuable for students. These resources not only provide the correct results but also offer detailed steps that explain the reasoning behind each solution. By reviewing these breakdowns, learners can understand the process and apply similar methods to other problems they encounter.
Building Problem-Solving Confidence
One of the key benefits of using solution guides is that they allow students to verify their work. Checking solutions after attempting a problem helps identify mistakes and clarifies where improvements can be made. This process fosters confidence, as learners can see their progress and correct any misunderstandings before moving on to more challenging tasks.
Reinforcing Key Concepts
Reviewing step-by-step solutions also reinforces important mathematical principles. Understanding how each operation contributes to the final answer helps solidify foundational knowledge and ensures that students can approach similar problems with a clear, structured mindset. By seeing different approaches to solving the same type of problem, learners can expand their problem-solving toolkit and tackle future tasks with greater ease.
Tips for Solving Algebra 2 Equations
When solving complex mathematical equations, a structured approach is crucial for achieving accurate results. By following key strategies and applying proven techniques, you can simplify the process and reduce the likelihood of making errors. This section outlines useful tips that can help you navigate through different types of problems more efficiently.
Key Strategies for Success

Mastering the basics and practicing regularly will allow you to tackle even the most complicated problems with ease. Below are some of the fundamental techniques for solving equations:
| Tip | Description |
|---|---|
| Identify the type of equation | Determine whether the equation is linear, quadratic, exponential, etc. This helps decide the appropriate method to use. |
| Simplify the equation | Before solving, combine like terms and remove unnecessary factors to make the equation easier to handle. |
| Isolate the variable | Move terms around to get the variable on one side of the equation, making it easier to solve for its value. |
| Check for extraneous solutions | After solving, verify your solutions by substituting them back into the original equation to ensure they are valid. |
Common Mistakes to Avoid
Even small errors can lead to incorrect results, so it’s important to stay focused and avoid common pitfalls. Here are a few mistakes to watch out for:
- Forgetting to apply the distributive property
- Misinterpreting signs when working with negative numbers
- Failing to check your work after solving
By following these strategies and being mindful of potential errors, you’ll be able to solve equations with greater confidence and accuracy.
Exploring Advanced Algebra 2 Concepts
As you progress in your mathematical studies, you will encounter more complex topics that require a deeper understanding of fundamental principles. These advanced concepts often build upon what you’ve already learned, introducing new methods and techniques to solve intricate problems. In this section, we will explore some of the key areas that challenge students at higher levels of study.
Key Advanced Topics to Explore
Some of the core areas you’ll encounter include:
- Rational expressions and equations
- Complex numbers and their properties
- Conic sections, such as parabolas and hyperbolas
- Logarithmic and exponential functions
- Sequences and series, including arithmetic and geometric progressions
Approaching These Topics Effectively
To tackle these more advanced concepts, it’s important to approach them with the right strategies:
- Start with a solid foundation: Ensure you understand the prerequisites before diving into more complex material.
- Break down each concept into manageable parts: Focus on one aspect of the topic at a time to avoid feeling overwhelmed.
- Practice regularly: Consistent practice is key to mastering advanced techniques and reinforcing your understanding.
- Seek out different perspectives: Sometimes exploring multiple approaches to a single problem can lead to a clearer understanding.
By focusing on these advanced areas and applying thoughtful strategies, you will be able to deepen your understanding and tackle more challenging problems with confidence.
Benefits of the Cpm Answer Key
Access to comprehensive solution guides can greatly enhance the learning process, especially when dealing with complex mathematical exercises. These resources provide a detailed breakdown of the steps involved in solving each problem, offering learners a clear understanding of the methods used to arrive at the correct results. By reviewing these solutions, students can identify mistakes, reinforce their knowledge, and develop more effective problem-solving skills.
One of the primary advantages of using such resources is the ability to verify your work. This not only helps you check for errors but also gives you the opportunity to understand the reasoning behind each step. By comparing your approach with the provided solution, you can learn new strategies for tackling similar challenges in the future.
Additionally, these solution guides often present multiple ways to approach a problem, which broadens your understanding and allows you to choose the most efficient method for each situation. This flexibility is crucial for mastering more advanced topics and building the confidence needed to solve even more complex tasks.
How to Check Your Work in Algebra 2
Verifying your solutions is an essential part of mastering any mathematical concept. It helps to ensure that you haven’t made mistakes along the way and strengthens your understanding of the material. Whether you are solving equations, simplifying expressions, or working with functions, checking your work allows you to identify errors early and improve your problem-solving skills.
Start by carefully reviewing each step of your process. Check for common mistakes like sign errors, incorrect operations, or missed steps. Often, a small oversight can lead to incorrect results. By retracing your steps, you can quickly spot where things went wrong and correct them.
Another effective strategy is to substitute your solution back into the original problem. This method confirms that your answer makes sense in the context of the equation or problem. If both sides of the equation match after substitution, you can be confident that your solution is correct. If not, go back and review your steps to find the source of the mistake.
Lastly, consider alternate methods for solving the problem. Sometimes, approaching a task from a different angle can reveal insights that were overlooked in the initial attempt. This not only helps verify your current solution but also deepens your understanding of the underlying concepts.
Using Cpm Answers to Improve Skills
Accessing detailed solutions for mathematical problems can serve as an invaluable learning tool. These solutions not only show the correct results but also provide step-by-step instructions that help clarify the methods used. By studying these detailed solutions, students can strengthen their problem-solving abilities and learn new techniques that can be applied to similar problems in the future.
One of the best ways to improve your skills is by comparing your approach to the solution provided. This comparison allows you to spot mistakes, understand where you may have gone wrong, and gain insight into more efficient strategies. By revisiting each step and understanding the rationale behind it, you can refine your approach to problem-solving and avoid making similar errors in the future.
Additionally, seeing the solution presented in multiple ways can deepen your understanding of the material. It shows you different methods of reaching the same outcome, giving you a broader toolkit for tackling problems. This exposure to varied approaches can enhance both your flexibility and confidence when facing more difficult challenges.
Common Mistakes in Algebra 2
As students advance in their mathematical studies, they often encounter more complex problems that can lead to common errors. These mistakes, while frequent, can be avoided with careful attention to detail and a deeper understanding of the underlying concepts. Recognizing and addressing these errors early can help improve problem-solving accuracy and prevent future misunderstandings.
Frequent Errors to Watch For
- Sign errors: One of the most common mistakes is mismanaging signs, especially when dealing with negative numbers or distributing across parentheses.
- Incorrectly applying rules: Misunderstanding the properties of exponents, logarithms, or fractions can lead to incorrect results.
- Forgetting to check solutions: It’s crucial to substitute your solution back into the original equation to ensure it satisfies the given conditions.
- Overlooking restrictions: Certain problems may have restrictions, such as no division by zero or only positive values, which can be easy to forget.
- Skipping steps: Rushing through problems or skipping intermediary steps may lead to missed mistakes and inaccurate solutions.
How to Avoid These Mistakes
- Double-check your work: Before finalizing your solution, go over each step to ensure you haven’t overlooked a detail.
- Write out all steps: Clearly showing your work can help you identify any mistakes and ensure that no crucial steps are skipped.
- Review basic concepts: Ensure that you have a solid understanding of key principles, as many errors stem from misapplying fundamental rules.
- Use multiple methods: Approaching a problem from different angles can help verify your solution and uncover any errors.
By remaining aware of these common pitfalls and practicing careful problem-solving strategies, you can reduce mistakes and build a more thorough understanding of advanced topics.
Practice Problems and Their Solutions
Solving practice problems is one of the best ways to reinforce your understanding of mathematical concepts. By working through problems, you can apply the theories you’ve learned and identify any areas where you need further clarification. Each problem offers a unique challenge, and reviewing the solutions allows you to see different methods of approaching similar tasks.
In this section, we’ll explore a variety of practice problems that will help strengthen your skills and understanding. We’ll also provide solutions with step-by-step explanations to guide you through the thought process behind each answer. This approach ensures that you not only arrive at the correct result but also learn how to approach problems in a methodical and efficient way.
Example Problem 1
Solve for x: 3x + 7 = 22
Solution
| Step | Explanation |
|---|---|
| 1 | Subtract 7 from both sides: 3x = 15 |
| 2 | Divide both sides by 3: x = 5 |
| 3 | The solution is x = 5 |
Example Problem 2
Solve for y: 2y – 4 = 10
Solution
| Step | Explanation |
|---|---|
| 1 | Add 4 to both sides: 2y = 14 |
| 2 | Divide both sides by 2: y = 7 |
| 3 | The solution is y = 7 |
These examples illustrate the importance of breaking down problems into manageable steps. By practicing similar problems, you’ll gain confidence in your ability to solve more complex equations and apply the correct strategies for each situation.
How Cpm Answers Help With Test Prep
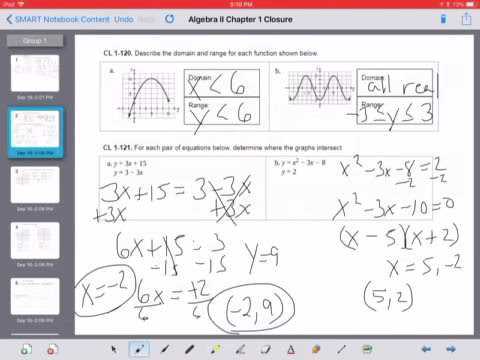
When preparing for exams, practicing problems and understanding the solutions are crucial for success. Using solution guides can offer valuable insight into the correct methods for solving complex problems, reinforcing learning, and boosting confidence. By following detailed explanations, students can improve their problem-solving strategies and identify areas where they may need additional practice.
These guides provide more than just the final answers–they offer step-by-step breakdowns that highlight common techniques, helping you to grasp the reasoning behind each step. This process builds a deeper understanding of the material, which is essential for performing well on tests and assessments.
Benefits of Using Solution Guides
- Reinforcement of Concepts: Reviewing detailed solutions reinforces key concepts, ensuring that you understand not just how to solve a problem but why a particular method works.
- Better Problem-Solving Skills: Step-by-step solutions help develop logical thinking, which can be applied to unfamiliar problems on tests.
- Confidence Boost: Seeing how to approach different problem types builds self-assurance, reducing test anxiety.
- Identification of Mistakes: Comparing your solution to a guide allows you to spot errors and avoid repeating them in future exercises.
- Time Management: Understanding the most efficient ways to solve problems can save time during a timed exam.
How to Use Solution Guides Effectively
- Work Through Problems First: Attempt problems on your own before checking the solutions. This allows you to actively engage with the material and identify areas of difficulty.
- Review Step-by-Step: Carefully read through the solution steps, making sure you understand each one before moving on to the next.
- Practice Similar Problems: After reviewing a solution, practice similar problems to reinforce the concepts and techniques learned.
- Focus on Understanding: Aim to understand the logic behind each step, not just memorize the methods. This deeper comprehension will help on tests with varying questions.
Incorporating solution guides into your study routine is an effective way to improve test performance. By understanding the methods behind problems and practicing regularly, you’ll be better prepared for any exam challenges that come your way.
Mastering Algebra 2 with Cpm Answers
Achieving proficiency in advanced mathematical concepts requires practice, understanding, and the right resources. One of the most effective ways to master these topics is by using comprehensive solutions that provide clear, step-by-step guidance. These resources not only help clarify complex ideas but also enable students to develop their problem-solving skills, building a solid foundation for more advanced material.
By studying these solutions, learners can improve their understanding of difficult problems, see multiple approaches to the same concept, and build confidence in their abilities. As they work through examples, students begin to recognize patterns and common techniques, which are key to solving problems quickly and accurately.
Benefits of Using Solution Guides
- Clear Step-by-Step Explanations: Seeing each step of a problem’s solution helps reinforce understanding and reveals the logical connections between concepts.
- Identifying Areas for Improvement: Reviewing solutions allows you to pinpoint areas where you may need extra practice, improving your overall grasp of the material.
- Building Problem-Solving Confidence: Repeated exposure to various problem types helps boost your ability to tackle unfamiliar questions on exams.
How to Effectively Use Solution Guides
To maximize the benefits of these solutions, follow these steps:
| Step | Action |
|---|---|
| 1 | Work Through Problems Independently: Attempt problems on your own first to test your understanding before checking the provided solutions. |
| 2 | Review Solutions Carefully: Go through each step of the solution process to understand why each method is used. |
| 3 | Practice Similar Problems: After reviewing the solution, practice more problems of the same type to reinforce your understanding and speed. |
| 4 | Seek Alternative Methods: Look for different ways to approach the same problem to deepen your understanding of the concept. |
Mastering mathematical topics takes time and effort. With the right approach and resources, however, you can significantly improve your skills, preparing yourself for both tests and future challenges in advanced studies.
Effectively Reviewing Algebra 2 Topics
To solidify your grasp on advanced mathematical concepts, regular and structured review is essential. The key to success lies in not just understanding the material, but being able to apply it confidently. By reviewing problems and revisiting key concepts, you can identify areas of strength and address weak points before moving on to more complex topics. Effective review is a continuous process that improves retention and prepares you for exams and real-world applications.
Rather than passively reading over your notes, actively engaging with the material through practice problems and explanations helps deepen your understanding. As you revisit the topics, focus on challenging areas and reinforce your knowledge through repetition and varied problem-solving techniques.
Tips for Efficient Topic Review
- Immediate Feedback: Students can quickly assess their understanding and correct mistakes in real-time.
- Self-Paced Learning: Learners can progress through problems at their own pace, revisiting challenging concepts whenever needed.
- Comprehensive Explanations: Many resources offer detailed solutions and explanations, which help clarify the reasoning behind each step.
- Increased Confidence: Knowing that a solution guide is available allows students to take risks in their learning without fear of making mistakes.
Alternative Resources for Algebra 2 Learning
When traditional textbooks or methods aren’t enough to fully grasp advanced mathematical concepts, exploring alternative resources can provide a fresh perspective. These additional materials often offer different explanations, practice problems, and interactive experiences that can cater to various learning styles. Whether you’re struggling with a specific concept or simply looking for more variety in your study routine, alternative resources can be a valuable tool in your educational journey.
Exploring online platforms, video tutorials, interactive problem sets, and even group study sessions can significantly enhance your understanding. With the wealth of resources available, students can choose the approach that works best for them, whether it’s through guided lessons, hands-on exercises, or peer collaboration.
Online Platforms and Websites
Numerous websites offer free or paid content to help learners understand and practice complex topics. These resources often include video explanations, step-by-step solutions, and exercises that provide immediate feedback. Popular platforms like Khan Academy, Coursera, and edX are just a few examples that offer comprehensive courses on advanced mathematics. They allow you to work at your own pace, revisit difficult topics, and track your progress.
Interactive Tools and Apps
Mobile apps and interactive websites can make learning more engaging. Tools such as Wolfram Alpha or Desmos allow students to visualize mathematical concepts, perform calculations, and explore various types of problems in a dynamic environment. These apps provide instant feedback, which helps to identify mistakes and improve understanding in real-time.
By utilizing these alternative learning tools, students can supplement their textbook knowledge and enhance their problem-solving skills, ultimately improving their performance in advanced mathematics courses.
How Educational Guides Support Self-Learning
Effective self-learning in advanced mathematics often requires both practice and immediate feedback. Educational guides, which provide solutions and explanations, can serve as crucial tools for independent study. These resources allow learners to check their work, identify mistakes, and understand the correct approach to solving problems. By using these guides, students can reinforce their learning, build confidence, and gradually improve their problem-solving abilities without relying solely on teachers or tutors.
One of the key benefits of using these resources is that they encourage active learning. Students can attempt problems on their own, consult the solutions for guidance, and then revisit areas where they encountered difficulties. This iterative process of trial, error, and correction helps to solidify concepts and enhances retention. Moreover, this method promotes a deeper understanding of the material, as students are not just memorizing answers, but also learning the reasoning behind each solution.
Benefits of Using Educational Guides
There are several advantages to utilizing educational guides in self-learning:
How to Make the Most of Educational Resources
To maximize the effectiveness of these guides, students should approach them strategically:
- Attempt Problems Independently: Always try to solve problems on your own first. This will help you understand your own thought process and identify areas of weakness.
- Use Solutions as a Learning Tool: When consulting the guide, don’t just look for the final answer. Focus on understanding the steps and reasoning behind each solution.
- Revisit Difficult Concepts: If you find certain problems challenging, review the explanations multiple times until the concept becomes clearer.
By following these strategies, students can leverage educational guides to enhance their understanding, improve their skills, and succeed in their self-directed learning journey.
Key Takeaways from Mathematical Problem Solutions
When reviewing solutions to mathematical problems, the focus should be on the underlying principles that guide the process. These solutions provide more than just the correct final answer–they reveal the strategies and reasoning behind each step. By understanding the methods used to reach the solution, students can improve their problem-solving skills and gain a deeper grasp of the concepts. Whether working through complex equations or geometric problems, these insights can significantly enhance learning and mastery of the subject.
Understanding the Process
One of the most valuable aspects of reviewing problem solutions is recognizing the logical flow behind each step. By breaking down the process, students can see how different concepts are interconnected and how to apply them in various situations. This approach encourages a more comprehensive understanding, helping students not only solve similar problems but also think critically about mathematical reasoning.
Common Mistakes to Avoid
While reviewing solutions, it’s essential to also learn from common errors. Some of the most frequent mistakes include:
- Misapplication of Formulas: Not all formulas work for every scenario, so it’s crucial to understand when and how to apply each one correctly.
- Skipping Steps: Rushing through calculations can lead to overlooked mistakes. Taking the time to complete each step ensures accuracy.
- Failure to Check Work: Even after solving a problem, reviewing your work helps catch simple errors that may have been missed during initial calculations.
By focusing on the reasoning behind each step and identifying common pitfalls, students can improve both their problem-solving techniques and overall understanding of the material.