Geometry Final Exam Review with Answers

Preparing for a challenging assessment in mathematics requires a clear understanding of key concepts and effective strategies to tackle a variety of problems. This section is designed to help you strengthen your skills and boost your confidence, guiding you through essential topics and common question types you will encounter. By focusing on crucial formulas, theorems, and practical approaches, you’ll be ready to face any challenge that comes your way.

Mastering the fundamentals is the first step in your preparation. From basic shapes and angles to more advanced principles, a solid foundation will allow you to approach more complex problems with ease. With the right techniques, you can streamline your problem-solving process, ensuring that you are not only accurate but also efficient in applying your knowledge.

Throughout this guide, you will find numerous examples, step-by-step explanations, and practice problems designed to reinforce your understanding. Emphasis will be placed on methods that help you break down complicated questions into manageable steps, allowing you to work through them methodically. Whether you’re looking to refresh your memory or dive deeper into specific topics, this guide offers a structured approach to help you succeed.

Geometry Final Exam Review with Answers

Success in any mathematical challenge requires a thorough understanding of core principles and the ability to apply them to a variety of problems. In this section, we focus on consolidating essential knowledge, practicing key techniques, and preparing you for the types of questions that are commonly encountered. This approach will help you feel confident and prepared as you work through problems of increasing complexity.

Key Concepts to Focus On

Mastering the foundational concepts is crucial for navigating complex problems. Begin by reviewing critical formulas and rules that govern shapes, angles, and their relationships. Understanding these basic principles allows you to identify patterns and recognize the most efficient solutions. Spend time practicing problems that test your grasp of these concepts to solidify your knowledge.

Practical Problem-Solving Strategies

Solving problems efficiently requires not only theoretical knowledge but also a clear approach to tackling questions. Break each problem down into manageable steps, and always look for shortcuts or techniques that can simplify the process. Whether it’s working through equations, analyzing diagrams, or applying theorems, a methodical approach will save time and help avoid common mistakes.

Essential Geometry Concepts to Master

To excel in any mathematical challenge, a solid grasp of fundamental ideas is essential. By understanding the core relationships between shapes, angles, and measurements, you can navigate through more complex problems with ease. These concepts form the backbone of problem-solving strategies and are frequently tested. Focus on mastering these ideas to build confidence and accuracy in your approach.

Concept	Description
Angles and Their Properties	Understand different types of angles, such as acute, obtuse, and right, and how to calculate their measures in various figures.
Area and Perimeter	Learn to compute the area and perimeter for basic shapes, including triangles, rectangles, and circles.
Triangle Properties	Familiarize yourself with the properties of various types of triangles, such as equilateral, isosceles, and scalene.
Quadrilaterals	Study the properties of different four-sided figures, including squares, rectangles, parallelograms, and trapezoids.
Solid Figures	Understand the key properties and formulas related to three-dimensional objects like cubes, spheres, and cones.

Key Formulas for Exam Success

Mastering important formulas is essential for solving a wide range of mathematical challenges efficiently. These formulas provide the foundation for quick calculations and accurate problem-solving, helping you save time and avoid mistakes. By memorizing and understanding the application of each formula, you can approach questions with confidence and improve your performance. Below are some of the most crucial formulas to focus on.

Formula	Description
Area of a Triangle	Area = 1/2 × base × height
Area of a Rectangle	Area = length × width
Circumference of a Circle	Circumference = 2 × π × radius
Area of a Circle	Area = π × radius²
Volume of a Rectangular Prism	Volume = length × width × height
Pythagorean Theorem	a² + b² = c² (for right-angled triangles)
Surface Area of a Sphere	Surface Area = 4 × π × radius²

Understanding Geometry Proofs

Proofs are the backbone of logical reasoning in mathematics, allowing you to establish the truth of a statement based on accepted principles. Mastering the process of constructing and understanding proofs is essential for solving complex problems and demonstrating mathematical relationships. A proof requires you to start from known facts and systematically build a case to reach a conclusion, using clear reasoning and a series of logical steps.

The structure of a proof typically includes a combination of definitions, postulates, and previously established theorems. It’s important to understand how each of these elements contributes to the overall argument. By practicing different types of proofs, such as direct proofs, indirect proofs, and proof by contradiction, you can improve your ability to navigate even the most intricate problems.

Commonly Tested Geometry Theorems

Understanding key theorems is crucial for solving many of the problems you’ll encounter. These fundamental principles are frequently tested and form the foundation of many mathematical arguments. Being familiar with these concepts and knowing how to apply them will make complex problems more manageable. Below are some of the most commonly encountered theorems that are essential for success.

Important Theorems to Know

• Pythagorean Theorem – This theorem relates the sides of a right triangle. It states that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
• Angle Sum Theorem – The sum of the interior angles of any triangle is always 180°.
• Parallel Postulate – If two lines are parallel to the same line, they are parallel to each other.
• Vertical Angles Theorem – Vertical angles are always equal to each other.
• Congruent Triangles Theorem – Two triangles are congruent if their corresponding sides and angles are equal.

Application of Theorems in Problem Solving

Each of these theorems can be applied in different scenarios, whether you’re working with triangles, parallel lines, or angles. Understanding their proofs and how to use them will help you in solving for unknown values or proving relationships between figures. Practice using these theorems with various problems to gain a deeper understanding of their applications and solidify your knowledge.

Tips for Solving Geometry Word Problems

Word problems often require you to translate a written description into a mathematical model. The key to success is breaking down the problem into smaller, manageable parts. With a methodical approach, you can extract the necessary information, apply the right formulas, and solve the problem efficiently. Here are some strategies to improve your ability to tackle these types of questions.

• Read Carefully: Pay attention to every detail in the problem. Look for keywords that indicate operations, such as “sum,” “difference,” “product,” or “quotient.”
• Draw a Diagram: Whenever possible, sketch a diagram based on the description. This can help visualize the relationships between different elements in the problem.
• Identify What You Need to Find: Clearly define the unknowns and what the problem is asking you to solve for. This will guide your approach to the solution.
• Translate Words into Equations: Convert the problem’s description into mathematical equations. Look for relationships between quantities and express them algebraically.
• Check Units and Labels: Always keep track of the units of measurement (e.g., inches, centimeters, degrees) and ensure your final answer is in the correct form.

By practicing these strategies and staying organized, you can simplify complex word problems and approach them with confidence. The more you work through, the more intuitive these steps will become, allowing you to solve problems more quickly and accurately.

Geometry Practice Problems with Solutions

Practicing problems is one of the best ways to reinforce your understanding and improve your problem-solving skills. In this section, you’ll find a series of practice questions designed to test various concepts and techniques. After each problem, a detailed solution will help you understand the reasoning behind each step, ensuring you can apply the knowledge to future challenges.

Problem 1: Area of a Triangle

Find the area of a triangle with a base of 10 cm and a height of 5 cm.

1. Solution: To find the area of a triangle, use the formula: Area = 1/2 × base × height.
2. Substitute the given values: Area = 1/2 × 10 × 5.
3. The area is 25 cm².

Problem 2: Perimeter of a Rectangle

Calculate the perimeter of a rectangle with a length of 8 meters and a width of 3 meters.

1. Solution: The perimeter of a rectangle is calculated with the formula: Perimeter = 2 × (length + width).
2. Substitute the given values: Perimeter = 2 × (8 + 3).
3. The perimeter is 22 meters.

Problem 3: Finding the Missing Angle

In a triangle, two of the angles are 45° and 65°. Find the third angle.

1. Solution: The sum of the angles in a triangle is always 180°.
2. So, Third angle = 180° – (45° + 65°).
3. The third angle is 70°.

Problem 4: Volume of a Cylinder

Find the volume of a cylinder with a radius of 3 cm and a height of 7 cm.

1. Solution: The volume of a cylinder is calculated with the formula: Volume = π × radius² × height.
2. Substitute the given values: Volume = π × 3² × 7.
3. The volume is approximately 197.92 cm³.

Problem 5: Solving for Unknown Side in a Right Triangle

In a right triangle, one side is 6 cm, and the hypotenuse is 10 cm. Find the length of the other side.

1. Solution: Use the Pythagorean theorem: a² + b² = c², where c is the hypotenuse.
2. Substitute the known values: 6² + b² = 10².
3. 36 + b² = 100
4. Subtract 36 from both sides: b² = 64.
5. Take the square root of both sides: b = 8.

By working through these problems, you’ll gain valuable practice and deepen your understanding of key concepts. Each solution provides the step-by-step reasoning that helps reinforce the methods used to arrive at the correct result.

Analyzing Diagrams for Exam Questions

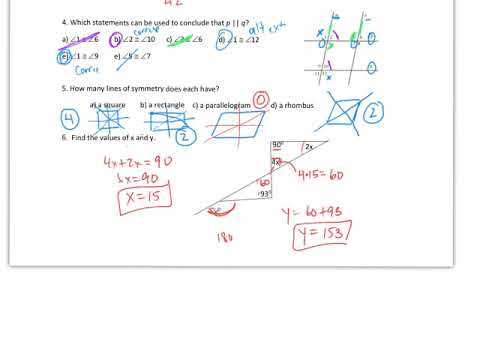
Diagrams are often included in problems to provide a visual representation of the situation, making it easier to understand relationships between different elements. Interpreting these visuals correctly is a crucial skill that can significantly simplify problem-solving. By breaking down the diagram, identifying key components, and translating them into mathematical relationships, you can approach the question more confidently.

Steps to Analyze Diagrams

• Identify Key Elements: Look for important points, lines, angles, and shapes within the diagram. These are typically the main components you will need to focus on.
• Label the Diagram: If the diagram isn’t already labeled, assign labels to key points, angles, and lengths. This can help keep track of the variables as you work through the problem.
• Understand the Relationships: Pay attention to any given conditions or properties, such as parallel lines, congruent angles, or special triangle types, which can influence how you solve the problem.
• Look for Symmetry or Patterns: Sometimes diagrams have symmetrical features or repeating patterns that can help you identify shortcuts or simplify calculations.

Common Diagrams and Their Uses

• Triangles: Often used to test properties like the Pythagorean theorem, angle relationships, and congruency.
• Circles: These can involve tangents, arcs, central angles, and inscribed angles. Look for key information such as radii or chord lengths.
• Polygons: Diagrams may represent quadrilaterals, regular polygons, or irregular shapes. Identifying parallel sides, perpendicular angles, or area formulas is often essential.
• Coordinate Geometry: Sometimes diagrams will include points on a coordinate plane, where you’ll need to apply distance or slope formulas.

By focusing on these strategies and practicing with a variety of diagrams, you’ll become more proficient at using visuals to solve problems efficiently and accurately. Properly interpreting the diagram often leads to faster and more accurate solutions, saving valuable time during assessments.

Types of Geometry Questions to Expect

When preparing for a test, it’s helpful to familiarize yourself with the different types of problems you may encounter. Questions can vary in format, ranging from simple calculations to more complex reasoning tasks. Understanding the various categories of problems will help you approach each one with the right strategies and techniques.

Common Problem Types

• Area and Perimeter Calculations: These problems require you to find the area or perimeter of various shapes such as rectangles, triangles, and circles. Be sure to know the key formulas for each shape.
• Angle Relationships: Expect questions about complementary, supplementary, vertical, and corresponding angles. These problems often involve identifying relationships between intersecting lines or parallel lines and transversals.
• Volume and Surface Area: Some questions will ask you to calculate the volume or surface area of three-dimensional objects like spheres, cones, cylinders, or prisms. You will need to apply specific volume and surface area formulas.
• Proofs and Theorems: Some problems will test your understanding of key properties and theorems. You may be asked to prove certain relationships or apply known theorems to derive new results, such as using the Pythagorean theorem or properties of similar triangles.

Problem-Solving Techniques

• Visualizing the Problem: Drawing diagrams is often the first step in solving problems, especially for angle and distance-related questions. Labeling important points or lines can simplify calculations and lead to quicker solutions.
• Using Formulas: For problems involving measurements, be sure to recall the necessary formulas. Knowing when to apply each formula (e.g., area, volume, perimeter) will save time and reduce errors.
• Identifying Relationships: Many problems involve understanding geometric properties like symmetry, congruence, or similarity. Recognizing these relationships allows you to use shortcuts and solve the problem more efficiently.
• Applying Logical Reasoning: Problems that involve proofs require careful reasoning and step-by-step justification. Practice using logical arguments to demonstrate the validity of your conclusions.

By understanding the types of questions likely to appear and developing strategies for each, you can approach your test with confidence. Practicing a variety of problem types will help you become more adept at identifying key concepts and applying the appropriate methods to find solutions.

How to Tackle Circle Geometry Problems

Circle-related problems often present unique challenges due to the complex relationships between various parts of the circle. To solve these problems effectively, it’s important to understand key concepts such as radii, diameters, tangents, chords, and arcs. By mastering these fundamentals, you’ll be better equipped to identify relevant information, apply appropriate formulas, and solve the problem step by step.

Key Concepts to Know

• Radius and Diameter: The radius is the distance from the center to any point on the edge, while the diameter is twice the length of the radius. Understanding these relationships is crucial for many circle problems.
• Tangents and Secants: A tangent is a line that touches the circle at exactly one point, while a secant intersects the circle at two points. Recognizing the differences and applying the relevant properties can simplify problem-solving.
• Arcs and Chords: An arc is a portion of the circle’s circumference, and a chord is a line segment connecting two points on the circle. Be familiar with the formulas for arc length and sector area, as well as the relationship between arcs and angles.
• Central and Inscribed Angles: Central angles are formed by two radii and measure the angle at the center of the circle, while inscribed angles are formed by two chords and measure the angle at the edge of the circle. These angles have important properties that help solve problems involving angles and segments.

Problem-Solving Strategies

• Draw the Diagram: When tackling circle-related questions, always start by sketching the circle and labeling known information. This visual aid will help you see relationships between elements and guide your next steps.
• Use the Right Formulas: Be familiar with common circle formulas such as the formula for the circumference (C = 2πr) and area (A = πr²), as well as formulas for arc length (L = θr) and sector area (A = ½θr²).
• Apply Angle Properties: Use properties of central and inscribed angles to solve for unknown values. For example, the central angle is equal to the arc it intercepts, and the inscribed angle is half of the central angle that subtends the same arc.
• Leverage Symmetry: Circles often exhibit symmetry, which can help simplify complex problems. Identifying symmetrical parts of the diagram can lead to shortcuts and reduce the amount of calculation needed.

By focusing on these core concepts and employing effective strategies, you can approach circle-related problems with confidence. Remember to practice different types of circle problems to develop a deeper understanding and improve your problem-solving skills.

Mastering Trigonometry in Geometry

Trigonometric concepts are essential tools for solving a variety of problems involving triangles and other shapes. By understanding the relationships between angles and side lengths, you can simplify complex calculations and find unknown values in geometric figures. Whether working with right triangles or more advanced shapes, mastering key trigonometric functions will significantly improve your ability to solve problems accurately and efficiently.

Core Trigonometric Functions

• Sine, Cosine, and Tangent: These are the fundamental functions for solving right triangles. The sine, cosine, and tangent functions relate the angles of a triangle to the ratios of its sides. Memorizing the basic definitions of these functions (opposite/hypotenuse for sine, adjacent/hypotenuse for cosine, and opposite/adjacent for tangent) is crucial for success.
• Inverse Trigonometric Functions: In addition to the basic functions, the inverse trigonometric functions help you find angles when given side lengths. The inverse of sine, cosine, and tangent are essential for calculating unknown angles in various geometric contexts.
• Trigonometric Identities: Familiarity with key identities, such as the Pythagorean identity (sin²θ + cos²θ = 1), allows you to simplify expressions and solve equations that involve trigonometric functions.

Problem-Solving Techniques

• Labeling Sides and Angles: Always start by labeling the sides and angles in your diagram. This makes it easier to identify which trigonometric function to use. For right triangles, use the opposite, adjacent, and hypotenuse sides based on the angle in question.
• Setting Up Equations: Once you’ve identified the appropriate function, set up an equation based on the given information. For example, if you’re given an angle and one side of a triangle, you can solve for the missing side by using the relevant trigonometric ratio.
• Using the Unit Circle: The unit circle is a powerful tool for solving trigonometric problems. Understanding how the sine and cosine values relate to the coordinates on the unit circle will help you solve a wide range of problems involving angles.
• Checking for Consistency: After solving for a side or angle, always double-check your results by substituting them back into the original equation or diagram. This helps ensure your solution is consistent and accurate.

By mastering these trigonometric concepts and strategies, you’ll be able to approach problems with confidence and clarity. Whether dealing with right triangles or more complex figures, these tools will help you unlock the solutions to a wide range of challenges.

Coordinate Geometry Exam Strategies

When solving problems related to points, lines, and shapes on a coordinate plane, it’s important to have a systematic approach. Success in this area depends on applying algebraic concepts to geometric problems, using formulas for distance, slope, and midpoints, and being able to visualize the relationships between points. A solid understanding of key concepts will help you navigate questions involving equations of lines, circles, and other geometric figures, ultimately improving your problem-solving efficiency.

Key Techniques for Success

• Mastering Basic Formulas: Knowing the fundamental formulas for distance, slope, and midpoint is essential. These tools allow you to quickly analyze relationships between points. The distance formula, for example, helps you calculate the length of a segment, while the slope formula gives insight into the steepness or direction of a line.
• Understanding Line Equations: Be comfortable with writing the equation of a line in both slope-intercept and point-slope form. This is a crucial skill for solving problems involving lines, as it allows you to find the equation of a line given certain information, or use the equation to identify unknowns.
• Visualizing the Problem: In many cases, drawing a clear, labeled diagram can significantly simplify the problem. Visualizing the location of points and lines on the coordinate plane can provide insight into the best approach for solving the problem, especially when asked to find intersections or distances.

Practical Tips for Common Problems

Below are some practical tips and reminders to keep in mind while solving common coordinate geometry problems:

Problem Type	Strategy
Finding Distance Between Two Points	Use the distance formula: d = √((x₂ – x₁)² + (y₂ – y₁)²) to find the straight-line distance between two points on the coordinate plane.
Finding Slope of a Line	Use the slope formula: m = (y₂ – y₁) / (x₂ – x₁) to calculate the slope between two points. A positive slope indicates an upward direction, while a negative slope indicates a downward direction.
Equation of a Line	Write the equation in slope-intercept form: y = mx + b, where m is the slope and b is the y-intercept. If you have a point and slope, use the point-slope form: y – y₁ = m(x – x₁).
Finding Midpoint Between Two Points	Use the midpoint formula: ((x₁ + x₂) / 2, (y₁ + y₂) / 2) to find the point exactly halfway between two given points.
Identifying Perpendicular Lines	Two lines are perpendicular if the product of their slopes equals -1. If one line has slope m₁, the other will have slope m₂ = -1/m₁.

By practicing these strategies and familiarizing yourself with key formulas, you’ll be better equipped to solve problems in coordinate-based contexts. Whether working with lines, shapes, or curves, these tools will help you find efficient solutions and improve your performance on related questions.

How to Approach Angle Theorems

Understanding the relationships between angles is fundamental for solving many problems in the realm of shapes and space. Various angle theorems can help simplify these relationships, providing a structured approach to finding missing angle measures, proving geometrical properties, or solving complex problems. To excel, it is important to familiarize yourself with the core principles that govern angle interactions and develop a systematic way to apply these principles effectively in problem-solving.

Key Angle Relationships to Remember

• Complementary Angles: Two angles are complementary if their measures add up to 90°. This relationship is useful when working with right angles or any setup where angles must sum to a right angle.
• Supplementary Angles: Two angles are supplementary if their measures sum to 180°. This is particularly useful in problems involving straight lines or adjacent angles on a line.
• Vertical Angles: When two lines intersect, the opposite angles formed are equal. These angles are often key to solving intersection problems or when proving angle relationships in polygons.
• Corresponding Angles: When a transversal intersects two parallel lines, the angles in matching positions are equal. This property helps in proving parallelism or calculating unknown angles in parallel line problems.

Approach and Strategy for Solving Angle-Based Problems

When confronted with problems involving angle relationships, follow a logical strategy to break down the problem efficiently:

• Identify Given Angles: Always begin by identifying all the angles and relationships provided in the problem. Mark known values on your diagram for clarity.
• Use Known Theorems: Apply relevant theorems to simplify the relationships between angles. For example, if two angles are complementary, set up an equation and solve for the unknown angle.
• Look for Angle Pairings: Angle relationships often come in pairs. Look for vertical, complementary, supplementary, or corresponding angles in your diagram to identify equal or related angles.
• Set Up Equations: Often, solving angle problems involves setting up equations based on angle relationships. Use algebraic methods to solve for unknowns.
• Check Your Work: Once you’ve solved for the unknown angles, check that all conditions of the problem are satisfied, such as the sum of angles in polygons or the properties of parallel lines.

Understanding Solid Geometry for the Exam

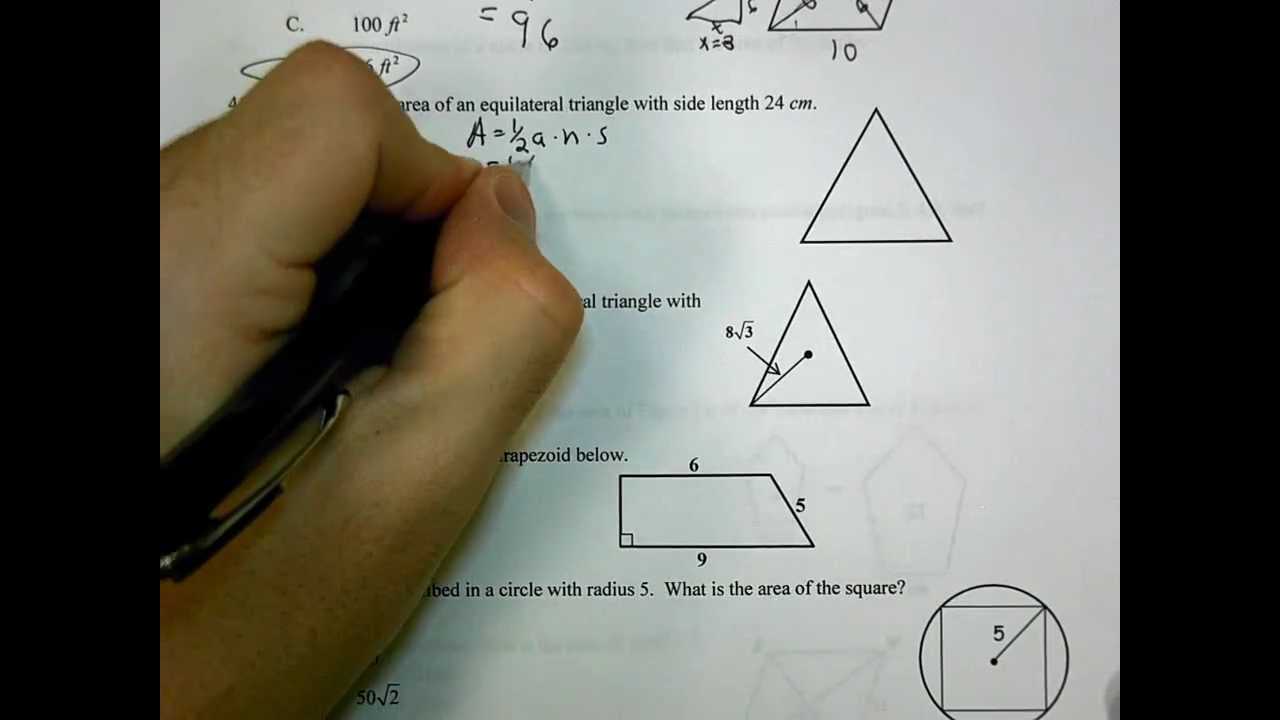
In problems involving three-dimensional shapes, it is essential to grasp the fundamental principles that govern their structure, volume, and surface area. Solid figures, unlike flat shapes, occupy space and are governed by different formulas and properties. Mastering how to calculate these quantities and understanding the relationships between the elements of three-dimensional objects will enhance your ability to solve related problems efficiently and accurately.

Key Solid Shapes and Their Properties

• Cuboid: A three-dimensional shape with six rectangular faces. The volume is found by multiplying length, width, and height, while the surface area is the sum of the areas of all six faces.
• Sphere: A perfectly round object. To find its volume, use the formula (4/3)πr³, where r is the radius. The surface area is calculated by 4πr².
• Cylinder: A shape with two circular bases and a height. The volume is given by πr²h, while the surface area is 2πr(h + r), where r is the radius and h is the height.
• Pyramid: A polyhedron with a polygonal base and triangular sides that meet at a point. Its volume is (1/3) × base area × height, and its surface area depends on the base shape and slant height of the sides.
• A three-dimensional object with a circular base and a pointed top. Its volume is (1/3)πr²h, and the surface area combines the area of the base and the lateral area (πr√(r² + h²)).

Approach to Solving Solid Figure Problems

• Visualize the Shape: Draw a diagram or look at a provided one. Label all known dimensions like radius, height, and edge lengths to help in applying formulas.
• Identify the Formula: Use the correct formula for the shape based on the question’s requirements, whether you need to find volume, surface area, or other properties.
• Substitute Known Values: Plug in the given values for the dimensions into the formula. Make sure all units are consistent (e.g., all in meters or centimeters).
• Check for Extra Conditions: Sometimes, the problem may include additional constraints or conditions like the relationship between different dimensions (e.g., diameter equals height). Make sure to factor these into your calculations.
• Use Estimation for Complex Problems: When dealing with complex objects or compound shapes, break the figure into simpler components, calculate each part’s volume or area, and then combine them to get the final result.

Time Management Tips for Geometry Exams

Effectively managing your time during a test is crucial to ensure you complete all questions while maintaining accuracy. Having a clear strategy for approaching different sections of a test can help reduce stress and improve your performance. By prioritizing tasks, pacing yourself, and keeping an eye on the clock, you can maximize your efficiency and avoid rushing through complex problems.

Set Priorities and Tackle Easy Questions First

Start by quickly scanning the entire test to get an overview. Identify the questions you find easiest and answer them first. This strategy helps build confidence and ensures that you secure marks for questions that you can solve quickly, leaving more time for difficult ones.

• Quickly answer basic calculations: If the question requires a simple calculation or applies a formula you’ve memorized, do it immediately to save time.
• Skip tricky questions temporarily: If you encounter a complex question, mark it and move on. Return to it later when you have more time to focus.

Allocate Time Based on Question Difficulty

Divide your available time according to the difficulty of each question. For instance, allocate more time for problems that require deeper thinking or multi-step solutions, and less time for straightforward ones. This will help ensure that you don’t spend too long on any one problem and leave enough time for the more challenging ones.

• Time yourself for each section: Divide your time into sections (e.g., 10 minutes for simple problems, 20 minutes for medium difficulty, and 30 minutes for harder ones). Stick to these limits.
• Don’t obsess over one problem: If you’re stuck, move on. Returning to the problem with a fresh mind often leads to new insights.

Stay Calm and Monitor the Clock

It’s easy to lose track of time when you’re focused on solving a problem, but it’s important to stay aware of the clock. Set a reasonable pace for each question and check the time periodically. This will help you gauge if you need to speed up or slow down as you approach the final questions.

• Keep a watch or timer: Having a reliable timepiece can help you stick to your plan without relying on the room clock, which may not always be visible.
• Be mindful of time remaining: In the last 10-15 minutes, prioritize answering any remaining questions, even if you have to make educated guesses.

Strategies for Multiple-Choice Questions

Multiple-choice questions can seem straightforward at first glance, but they often require careful analysis and strategic thinking. These types of questions assess your understanding of concepts, and with the right approach, you can efficiently eliminate incorrect options and identify the correct answer. By following a systematic approach, you can maximize your chances of success.

Process of Elimination

One of the most effective strategies for multiple-choice questions is the process of elimination. Even if you’re unsure of the correct answer, eliminating obviously incorrect options can significantly increase your chances of selecting the right one.

• Cross out unlikely answers: Look for options that are clearly irrelevant or logically impossible. These choices are usually designed to mislead.
• Compare remaining options: After eliminating the obvious incorrect answers, focus on the remaining options and compare them based on what you know.
• Use educated guesses: If you’re left with two possible answers, take your best guess based on the knowledge you have.

Look for Keywords in the Question

Pay attention to keywords or phrases in the question that can help guide you toward the correct answer. Often, the wording of the question itself can give you hints about which option is correct.

• Identifying qualifiers: Words like “always,” “never,” “some,” and “most” can change the meaning of the question and influence which choice is correct.
• Be wary of extreme statements: Answers that use absolute terms like “never” or “always” are often incorrect, as they’re rarely true in most scenarios.

Double-Check Your Work

If time permits, always review your answers before submitting. Sometimes, upon revisiting a question, you may catch small errors in your reasoning or notice a more obvious correct answer that you missed initially.

• Trust your first instinct: If you initially ruled out a choice for a solid reason, stick with your decision. Changing your answer too often can lead to mistakes.
• Check for consistency: If a question involves calculations or reasoning from earlier in the test, make sure your answer is consistent with your previous responses.

Reviewing Practice Tests

When preparing for a challenging assessment, it’s essential to actively engage with sample questions to familiarize yourself with the types of problems that might appear. Practicing through mock tests or past questions helps you identify areas of strength and weakness, improving both speed and accuracy. By simulating the real test environment, you can gain confidence and develop strategies to approach difficult questions effectively.

Benefits of Practice Tests

Working through practice tests not only helps reinforce your knowledge but also teaches you how to manage your time effectively under pressure. Each question presents an opportunity to identify patterns in the material and refine your problem-solving approach. Here are some advantages:

• Boosts confidence: The more familiar you become with the format, the more comfortable you’ll feel when the actual assessment takes place.
• Identifies weaknesses: Practice tests highlight specific areas where you may need additional study or practice.
• Improves time management: Repeated practice helps you gauge how long to spend on each section, so you’re less likely to run out of time.

How to Analyze Your Results

After completing a practice test, it’s important to spend time reviewing your answers. Simply knowing whether your response was correct or incorrect isn’t enough. Understanding why an answer was right or wrong allows you to improve and avoid similar mistakes in the future. Here’s how to make the most out of your analysis:

Step	Action
1	Identify incorrect responses and carefully analyze the reasoning behind the correct answer.
2	Revisit the corresponding sections of the material to reinforce your understanding of key concepts.
3	Practice similar problems to ensure that you can apply the correct approach consistently.
4	Track your progress over multiple tests to measure improvement and adjust your focus accordingly.

By carefully analyzing your performance, you can pinpoint areas where you need more practice and develop a targeted study plan to improve. This iterative process ensures that you’re fully prepared when the time comes to apply your knowledge in the actual assessment scenario.