Quantitative Methods Exam Questions and Answers

Success in any academic evaluation relies heavily on a solid understanding of key concepts and effective problem-solving skills. Whether you’re preparing for a comprehensive assessment or focusing on specific topics, a strategic approach to studying can make all the difference. By familiarizing yourself with core principles, practicing through exercises, and learning how to tackle complex scenarios, you can build the confidence needed to excel.

Critical thinking and the ability to apply theoretical knowledge to practical situations are central to mastering any challenging subject. Through the application of various techniques, it’s possible to break down even the most complex tasks into manageable steps. Focusing on conceptual understanding rather than rote memorization enhances retention and improves performance during assessments.

Preparing for any type of academic challenge requires both knowledge and strategy. A combination of understanding fundamental ideas, practicing with relevant examples, and refining test-taking techniques can significantly boost your chances of success. This approach will not only help you navigate the subject matter more effectively but also improve your ability to think critically under pressure.

Overview of Quantitative Methods

In any field that involves data analysis and interpretation, understanding the principles behind numerical calculations is essential. These principles form the foundation for solving a wide range of complex problems by breaking them down into smaller, more manageable parts. By applying specific techniques, it’s possible to derive meaningful insights from raw data and make informed decisions based on statistical reasoning.

At its core, this area of study focuses on the use of various tools to interpret numerical data. The key objective is to understand patterns, relationships, and trends that can be applied to real-world situations. Different approaches and techniques allow for systematic analysis of data, enabling clearer decision-making processes.

• Data Collection: Gathering accurate data through surveys, experiments, or observations.
• Data Analysis: Using tools to examine the data and uncover meaningful relationships.
• Statistical Inference: Drawing conclusions from data through models and estimations.
• Predictive Modeling: Applying mathematical models to predict future trends.

Overall, mastering this discipline involves developing a deep understanding of the techniques used to analyze data. It’s not just about calculating figures but also about interpreting results accurately and applying them in practical situations. These skills are valuable across a variety of sectors, from economics to healthcare, ensuring that decisions are based on sound, analytical evidence.

Key Topics in Quantitative Analysis

When diving into numerical analysis, there are several fundamental concepts that form the backbone of the subject. These core areas are essential for anyone looking to master the art of working with data. A clear understanding of these topics is necessary for accurate interpretation and effective application in various real-world contexts.

Probability theory is one of the most foundational concepts, as it allows for the assessment of uncertainty and the likelihood of various outcomes. Mastering probability distributions, random variables, and expected values enables individuals to model different scenarios and make informed predictions.

Statistical inference is another critical area, which involves making conclusions or generalizations about a population based on a sample. Techniques like hypothesis testing and confidence intervals are used to draw insights from data and assess the reliability of results.

• Descriptive statistics: Summarizing and presenting data through measures such as mean, median, mode, variance, and standard deviation.
• Regression analysis: Investigating relationships between variables and predicting future trends based on historical data.
• Sampling techniques: Methods for selecting representative subsets of data to make broader conclusions without needing to examine the entire population.
• Time series analysis: Analyzing data points collected or recorded at specific time intervals to identify trends, seasonal patterns, or cyclical behavior.

Familiarity with these areas not only improves the accuracy of conclusions but also ensures that data is interpreted in a way that supports sound decision-making. Each of these topics plays a vital role in transforming raw data into actionable insights, making them indispensable in any analytical process.

Essential Formulas for Exam Success

Mastering key equations is crucial for tackling complex problems efficiently. These formulas serve as the foundation for solving a wide range of problems, helping to streamline the process and avoid common mistakes. Understanding when and how to apply these critical formulas is essential for both accuracy and speed during assessments.

Among the most important are those used to calculate measures of central tendency, such as the mean, median, and mode. These are essential for summarizing data and identifying patterns within large datasets. Similarly, understanding how to compute variance and standard deviation is key to assessing the spread of data points around the mean.

• Mean: The sum of all values divided by the total number of values.
• Variance: The average squared deviation of each value from the mean.
• Standard Deviation: The square root of the variance, providing a measure of data spread.
• Linear Regression Equation: y = mx + b, used for predicting values based on relationships between variables.
• Confidence Interval: A range of values used to estimate a population parameter with a specified level of certainty.

By familiarizing yourself with these essential formulas, you can approach problems with greater confidence, ensuring that you make fewer errors and maximize your potential for success. Regular practice with these equations is key to developing fluency and achieving accurate results under pressure.

Understanding Statistical Distributions

Grasping how data behaves and is distributed across a population is fundamental to analyzing and interpreting information. Statistical distributions offer a framework for understanding how values are spread and where most data points tend to cluster. By examining these distributions, one can make predictions, assess patterns, and draw conclusions about a dataset’s characteristics.

There are several common types of distributions, each with unique properties that make them suitable for different types of data. These distributions help explain not only the central tendency but also the variability and the likelihood of various outcomes occurring within a dataset.

Types of Distributions

• Normal Distribution: A symmetric bell-shaped curve where most of the data points cluster around the mean.
• Binomial Distribution: Describes the number of successes in a fixed number of trials, often used for binary outcomes.
• Poisson Distribution: Used for modeling the number of events that occur within a fixed interval of time or space.
• Uniform Distribution: All outcomes are equally likely to occur, often represented by a rectangular shape.

Key Properties of Distributions

• Mean: The average value, representing the central point of the distribution.
• Variance: A measure of how spread out the data points are from the mean.
• Skewness: The degree to which the distribution deviates from symmetry.
• Kurtosis: The “tailedness” of the distribution, indicating how extreme the data points are relative to the mean.

Understanding these distributions allows analysts to select the appropriate model for their data, make more accurate predictions, and assess the uncertainty of their results. Mastering these concepts is essential for tackling complex analysis tasks and drawing reliable conclusions from data.

Approaches to Hypothesis Testing

Testing a hypothesis involves making an assumption about a population and using sample data to determine whether the assumption holds true. This process helps researchers make evidence-based decisions and draw conclusions about trends or relationships in data. Hypothesis testing is crucial for validating theories and supporting scientific or statistical claims.

There are several approaches used to evaluate hypotheses, each with specific steps and techniques. Understanding how to choose the appropriate method is essential for accurate analysis and interpretation of results.

Key Steps in Hypothesis Testing

• Formulating Hypotheses: Establishing a null hypothesis (H0) and an alternative hypothesis (H1), where the null typically represents no effect or difference.
• Choosing a Significance Level: Determining the threshold (usually 0.05) for accepting or rejecting the null hypothesis based on the probability of an observed result occurring by chance.
• Selecting the Test: Choosing the appropriate statistical test, such as a t-test, chi-square test, or ANOVA, based on the data type and research question.
• Analyzing the Data: Using the selected test to evaluate the sample data and calculate the test statistic.
• Making a Decision: Comparing the p-value to the significance level to determine whether to reject or fail to reject the null hypothesis.

Types of Hypothesis Tests

• t-Test: Used to compare the means of two groups to determine if there is a statistically significant difference between them.
• Chi-Square Test: Used for categorical data to assess whether observed frequencies differ significantly from expected frequencies.
• ANOVA: A method for comparing means across three or more groups to determine if there is a significant difference among them.
• Correlation and Regression Tests: Used to assess relationships between variables and to predict one variable based on another.

These techniques form the basis for rigorous testing in many fields, providing a structured approach to validating claims and making informed decisions based on data. Properly applying these methods ensures that the conclusions drawn are scientifically valid and statistically reliable.

Commonly Asked Exam Questions

Understanding the types of inquiries frequently posed in assessments can help you focus your preparation on the most critical areas. These questions are designed to test your ability to apply key concepts, analyze data, and solve complex problems efficiently. Familiarity with typical topics can also improve your speed and confidence when tackling challenges during the assessment.

Some questions are designed to assess fundamental concepts, while others challenge you to apply what you’ve learned to more complex or real-world scenarios. Being prepared for both types will ensure that you’re ready to approach any problem with the right techniques and reasoning.

Conceptual Questions

• Explain the difference between correlation and causation.
• What are the assumptions behind regression analysis?
• Define the central limit theorem and its importance in hypothesis testing.
• What is the purpose of a confidence interval?

Practical Application Questions

• Given a set of data, calculate the mean, variance, and standard deviation.
• Interpret the results of a hypothesis test, including the p-value and decision-making process.
• Describe how you would use linear regression to predict future outcomes based on historical data.
• Apply a t-test to compare two sample groups and explain your findings.

By practicing these types of questions, you’ll become more comfortable with the material and improve your ability to respond accurately under time pressure. Focused practice can significantly enhance your performance, ensuring you’re well-prepared for any assessment.

Sampling Methods in Quantitative Research

In any type of research involving numerical data, selecting the right sample is essential for ensuring that conclusions drawn from a subset accurately represent the larger population. The way in which participants or data points are chosen influences the validity and reliability of the findings. Understanding various sampling strategies is crucial for designing studies that yield meaningful, generalizable results.

Different sampling techniques are employed depending on the research objectives, available resources, and the nature of the population being studied. Each method has its strengths and limitations, and knowing when to apply each one can greatly improve the quality of the research.

Types of Sampling Methods

Sampling Method	Description	Advantages	Disadvantages
Random Sampling	Every individual has an equal chance of being selected.	Minimizes bias, increases representativeness.	Can be time-consuming and resource-intensive.
Stratified Sampling	Population is divided into subgroups, and random samples are taken from each subgroup.	Ensures key subgroups are represented.	More complex and time-consuming than simple random sampling.
Systematic Sampling	Every nth member is selected from a list or population.	Simple and easy to implement.	May introduce bias if there is a hidden pattern in the population.
Cluster Sampling	Population is divided into clusters, and entire clusters are randomly selected.	Cost-effective, useful for large populations.	Can lead to less precision compared to other methods.
Convenience Sampling	Sampling based on availability and ease of access.	Quick and inexpensive.	High risk of bias and lack of generalizability.

Choosing the Right Sampling Method

The choice of sampling strategy depends on the specific objectives of the study and the constraints faced by the researcher. For instance, random sampling is ideal when aiming for a truly representative sample, whereas convenience sampling may be used in exploratory studies where time and budget are limited. Regardless of the method, researchers must always account for potential biases to ensure that their findings are accurate and reliable.

Data Collection Techniques Explained

Gathering reliable and accurate data is the cornerstone of any research process. The techniques used to collect this data can vary depending on the research objectives, the nature of the information being sought, and the available resources. A strong understanding of the different approaches allows researchers to choose the best methods for their specific needs, ensuring the integrity and validity of their findings.

Each data collection technique offers unique advantages and challenges. It is crucial to evaluate the context and purpose of the research when deciding which technique to apply. By selecting the most appropriate strategy, researchers can ensure that they gather data that is both meaningful and relevant to the research question.

Primary Data Collection Techniques

• Surveys: Questionnaires or interviews are commonly used to gather responses from a sample population. Surveys can be administered in person, by phone, or online, and they are ideal for collecting large amounts of data quickly.
• Observations: Researchers collect data by observing subjects in their natural environment without interference. This technique is often used in behavioral research and can provide rich, real-time insights.
• Experiments: Controlled trials are conducted to examine cause-and-effect relationships. This technique is often used in scientific and medical research to test hypotheses under specific conditions.

Secondary Data Collection Techniques

• Document Review: Analyzing existing reports, articles, and historical records to extract relevant data. This method is useful for longitudinal studies or when primary data collection is not feasible.
• Archival Research: Involves examining past data from sources such as government databases, industry reports, or previous research studies. This method provides valuable insights without the need for new data collection.

Each of these techniques requires careful planning and consideration to ensure data accuracy and relevance. The chosen method must align with the study’s goals, time frame, and resource availability, while also addressing potential biases and ensuring ethical standards are met.

Interpreting Regression Results

Understanding the outcomes of a regression analysis is essential for drawing meaningful conclusions from data. Regression allows researchers to assess the relationships between variables and determine how changes in one or more predictors influence an outcome. Interpreting these results requires careful attention to several key statistical measures that describe the strength, direction, and significance of these relationships.

After performing a regression analysis, the results typically include coefficients, p-values, R-squared values, and other statistical indicators. Each of these components provides valuable insights into the nature of the relationships in the data and helps researchers make informed decisions based on the analysis.

Key Components of Regression Output

• Regression Coefficients: These values indicate the change in the dependent variable for a one-unit change in the independent variable, holding other factors constant. A positive coefficient suggests a positive relationship, while a negative one indicates an inverse relationship.
• p-Value: The p-value helps determine whether the relationship between the variables is statistically significant. A p-value less than 0.05 generally indicates a significant relationship, suggesting that the observed effect is unlikely to be due to random chance.
• R-squared: This statistic represents the proportion of variance in the dependent variable explained by the independent variables. An R-squared value closer to 1.0 indicates a better fit of the model, whereas a lower value suggests that the model explains less of the variation.

Assessing Model Fit and Assumptions

• Adjusted R-squared: Unlike the R-squared value, the adjusted R-squared takes into account the number of predictors in the model, making it useful for comparing models with different numbers of variables.
• Standard Error: This measure helps assess the accuracy of the regression coefficients. A smaller standard error suggests more precise estimates, while a larger standard error indicates greater uncertainty in the coefficient estimates.
• Residuals: Analyzing the residuals–differences between observed and predicted values–can help identify issues with the model, such as non-linearity or heteroscedasticity.

By examining these elements, researchers can draw meaningful conclusions about the relationships between variables, test hypotheses, and assess the validity of their models. Effective interpretation of regression results enables better decision-making and more accurate predictions based on the data at hand.

Common Errors in Quantitative Exams

In assessments that involve complex calculations and data analysis, students often encounter pitfalls that can impact their performance. Many mistakes arise from a misunderstanding of concepts, misinterpretation of instructions, or simple computational errors. Recognizing these common issues can help prevent them and improve overall results.

Some mistakes are due to rushing through problems without fully understanding the steps required. Others stem from neglecting key assumptions or overlooking details in the provided information. A careful approach to each problem can help mitigate these errors and ensure more accurate solutions.

• Misunderstanding Formulas: One of the most frequent errors occurs when students apply the wrong formula or misinterpret the terms within a formula. This can lead to incorrect results and wasted time.
• Incorrect Data Interpretation: Misreading or misinterpreting data, such as failing to understand the scale or units of measurement, can cause significant errors in calculations and conclusions.
• Overlooking Assumptions: Many tasks involve underlying assumptions that are crucial for solving the problem. Failing to account for these assumptions can lead to flawed outcomes and incorrect reasoning.
• Calculation Mistakes: Simple arithmetic errors, such as adding or multiplying numbers incorrectly, can throw off entire solutions, especially when dealing with large datasets.
• Ignoring Statistical Significance: Some students overlook the importance of testing the significance of their results, leading to conclusions that are not supported by the data.
• Failure to Check Units: Units are critical in many calculations, and failing to properly convert or match units can result in inconsistent or inaccurate results.
• Skipping Steps: In an attempt to finish quickly, students may skip intermediate steps in calculations. This can lead to missed opportunities to catch mistakes and verify results along the way.

By becoming aware of these common errors, students can take proactive steps to avoid them. Practicing careful analysis, double-checking work, and taking the time to thoroughly understand the material are key strategies for improving performance in such assessments.

Time Management for Quantitative Exams

Effective time management is crucial when tackling assessments that require complex calculations and data analysis. Without proper planning and organization, it’s easy to become overwhelmed or rush through tasks, leading to mistakes or incomplete answers. Being able to allocate time efficiently across all sections of the assessment can significantly impact performance and reduce stress.

One key to managing time effectively is understanding the types of problems presented and how much time is likely required for each. By estimating how long each question or task will take, students can prioritize their efforts, ensure they don’t spend too much time on one problem, and still have enough time for the entire test.

• Divide and Conquer: Break the assessment into sections and tackle the easier problems first. This builds confidence and leaves more time for the more challenging tasks later.
• Set Time Limits: Allocate a specific amount of time to each section or problem based on its difficulty. Stick to these limits to avoid spending too much time on any one part of the assessment.
• Practice Under Time Constraints: Familiarize yourself with the format and timing of the test by practicing under timed conditions. This helps develop a sense of how long tasks should take and improves overall speed.
• Identify Key Areas: Focus on sections where you are most confident or where the majority of points are awarded. Prioritize these areas to ensure you don’t miss out on easy marks.
• Skip and Return: If a question seems too time-consuming, skip it and move on to the next one. Return to it once the easier tasks are completed, giving yourself more time to focus on solving the harder problems.
• Stay Calm and Focused: Time pressure can lead to anxiety, which affects decision-making. Maintain a steady pace, breathe deeply, and avoid rushing.

By implementing these strategies, students can manage their time more effectively and complete all tasks within the allotted time, maximizing their chances of achieving a high score in data-driven assessments.

How to Tackle Word Problems

Word problems can often seem daunting, especially when they involve complex numbers and multiple steps. However, breaking down the problem into smaller, manageable parts makes it easier to understand and solve. A methodical approach is key to identifying the important information, organizing it effectively, and arriving at the correct solution.

Step 1: Read and Understand the Problem

Before attempting to solve any problem, it’s important to read it carefully. Pay close attention to the details, such as units of measurement, relationships between variables, and any specific instructions. Underlining or highlighting key information can help you stay focused on the essential elements of the problem.

Step 2: Identify What is Being Asked

Often, word problems may contain extra information that isn’t necessary for solving the problem. Determine what the question is really asking and identify the variables or unknowns you need to solve for. This will give you a clear direction for the next steps.

• Break the Problem into Steps: Identify each step in the problem and tackle them sequentially. Avoid trying to solve everything at once.
• Translate Words into Mathematical Expressions: Many word problems require translating phrases into equations. Look for keywords such as “total,” “difference,” or “sum” to guide your translation.
• Double-Check Units: Ensure that all units of measurement are consistent throughout the problem. Convert units if necessary to avoid confusion later.
• Verify the Solution: After solving, double-check your calculations and ensure that the answer makes sense in the context of the problem. Look over your work for any potential errors or misinterpretations.

By following these steps, you can make solving word problems more manageable and ensure accurate results. With practice, the process becomes more intuitive, making it easier to tackle even the most challenging scenarios.

Improving Exam Preparation Strategies

Effective preparation is the foundation of success in any assessment that involves analytical problem-solving. Developing a well-structured study plan, practicing regularly, and identifying areas for improvement are essential steps in achieving better results. A proactive approach ensures that you not only understand the material but also become confident in applying the concepts under time pressure.

One of the most important aspects of preparing for a test is consistency. Rather than cramming the night before, break your study sessions into manageable chunks over time. This allows for deeper learning and better retention of the material. Incorporate a variety of resources, such as textbooks, online tutorials, and practice tests, to get a well-rounded understanding of the subject.

• Set Clear Goals: Establish what you aim to achieve during each study session. Whether it’s mastering a specific topic or solving a set number of problems, clear goals help keep you focused.
• Practice Regularly: Consistent practice is key to building familiarity with the format and types of problems you will face. The more you practice, the quicker and more accurate your responses will become.
• Simulate Real Conditions: Try taking practice tests under timed conditions to replicate the pressure of the actual assessment. This will help you manage your time more effectively during the real test.
• Review Mistakes: Mistakes offer valuable insight into areas where you need improvement. Take time to review errors and understand why they occurred to prevent them in the future.
• Use Study Aids: Study guides, flashcards, or online resources can provide additional help in reinforcing concepts. Visual aids such as charts and diagrams can also simplify complex ideas.

By refining your approach and incorporating these strategies into your study routine, you can enhance your ability to tackle challenges with confidence and efficiency. Success is built on both preparation and the ability to adapt to different problems on the day of the assessment.

Study Resources for Quantitative Methods

Effective preparation for assessments that involve analytical problem-solving requires access to reliable resources. Utilizing the right tools can help reinforce your understanding of complex concepts, improve problem-solving skills, and enhance your overall performance. Whether you prefer textbooks, online platforms, or interactive exercises, a wide range of materials can support your learning journey.

One valuable resource is textbooks, which often provide detailed explanations, worked examples, and practice problems. They offer a structured approach to learning, allowing you to progress at your own pace. Supplementing your study with online platforms can provide interactive tools, video tutorials, and practice exercises that cater to different learning styles. These platforms often include quizzes that simulate real-world scenarios, helping you become more familiar with the types of challenges you will face.

• Textbooks: Comprehensive guides that cover foundational topics and advanced concepts. Look for books with clear explanations and a wide variety of practice problems.
• Online Courses: Websites like Coursera, Udemy, and Khan Academy offer courses on data analysis, statistics, and other related fields, which can be a great way to build knowledge from the ground up.
• Practice Problems: Websites like Brilliant.org and Project Euler provide practice problems that target key concepts and techniques used in real-world scenarios.
• Study Groups: Collaborating with peers can enhance understanding through discussion and shared problem-solving approaches. Group studies allow you to tackle difficult topics from different angles.
• Academic Journals: Reading research papers and academic journals can deepen your understanding of the theoretical aspects and give you exposure to advanced applications of the concepts.

With the right resources at your disposal, you can enhance your comprehension, refine your skills, and be better prepared to face any challenge that comes your way. Combining different study materials helps reinforce learning and provides diverse perspectives on the topics at hand.

Understanding Descriptive Statistics

Descriptive analysis involves summarizing and interpreting large sets of data to uncover patterns, trends, and meaningful insights. By using a variety of statistical measures, this approach simplifies complex datasets, making them easier to understand and communicate. Whether it’s determining the central tendency, variability, or overall distribution of a dataset, descriptive tools provide a clear overview that helps in making informed decisions.

The main goal of descriptive analysis is to present key information in a way that highlights important features of the data. This can be achieved using several key metrics, such as the mean, median, mode, standard deviation, and range. These tools allow analysts to get a better sense of the data’s central tendencies and variability, helping to set the stage for deeper analysis or hypothesis testing.

Key Measures in Descriptive Statistics

The following are the core statistical measures commonly used to summarize data:

• Mean: The arithmetic average of a set of values, calculated by summing all values and dividing by the number of observations.
• Median: The middle value when the data is arranged in ascending or descending order. It is particularly useful when the dataset contains outliers.
• Mode: The value that appears most frequently in a dataset, useful for identifying the most common observations.
• Standard Deviation: A measure of how spread out the values in a dataset are. It indicates the degree of variation from the mean.
• Range: The difference between the highest and lowest values in a dataset, providing a simple measure of the data’s spread.

Example of Descriptive Statistics

To demonstrate these measures, consider the following dataset representing the ages of a group of individuals:

Age	Frequency
22	3
25	5
28	4
30	2

From this dataset, we can calculate the following:

• Mean: (22*3 + 25*5 + 28*4 + 30*2) / (3+5+4+2) = 26.42
• Median: 25 (the middle value when arranged in ascending order)
• Mode: 22 (the most frequent value)
• Standard Deviation: A calculated measure indicating how spread out the data is around the mean.
• Range: 30 – 22 = 8

These statistical measures provide a simple yet powerful way to summarize and understand large datasets, serving as the foundation for further data analysis.

Using Graphs and Charts Effectively

Visual representations are a powerful tool for conveying data in a clear and digestible format. Graphs and charts can turn complex numerical information into intuitive visuals that highlight patterns, trends, and relationships. When used correctly, they can enhance understanding, make comparisons easier, and reveal insights that might be hidden in raw data.

To maximize the effectiveness of these visual tools, it’s important to choose the right type based on the nature of the data and the story you want to tell. For instance, bar charts are ideal for comparing different categories, while line graphs excel at showing changes over time. Pie charts are useful for illustrating proportions within a whole, and scatter plots are helpful in understanding correlations between two variables. Each type serves a unique purpose and should be selected carefully to ensure clarity and accuracy.

Best Practices for Creating Graphs and Charts

• Keep it Simple: Avoid cluttering the chart with unnecessary elements. Focus on the key data points to keep the visual clear and easy to interpret.
• Label Clearly: Always include descriptive titles, axis labels, and legends where necessary. This ensures the viewer knows what the chart represents and how to interpret it.
• Use Appropriate Scales: Make sure the scale of your graph is appropriate for the data range. Using inconsistent or misleading scales can distort the message.
• Choose the Right Chart Type: Select the chart that best fits the data. For example, time-series data is best represented by line graphs, while categorical data suits bar charts.
• Highlight Key Trends: Use colors or annotations to emphasize the most important aspects of the data. This draws attention to the key takeaways and makes the chart more impactful.

Examples of Effective Graph Usage

Consider the following scenarios where graphs and charts can be used effectively:

• Sales Performance Over Time: A line graph could illustrate how sales figures have evolved over the past year, allowing easy identification of trends and seasonal fluctuations.
• Market Share Distribution: A pie chart can effectively show the percentage of market share held by different companies in a given industry.
• Product Comparison: A bar chart is ideal for comparing multiple products or services across various categories, such as price, performance, or customer satisfaction.
• Customer Preferences: A scatter plot could help visualize the relationship between customer age and spending habits, providing insights into how different groups make purchasing decisions.

By following these best practices and choosing the right tools, graphs and charts can become indispensable in presenting data effectively and making complex information accessible to a wider audience.

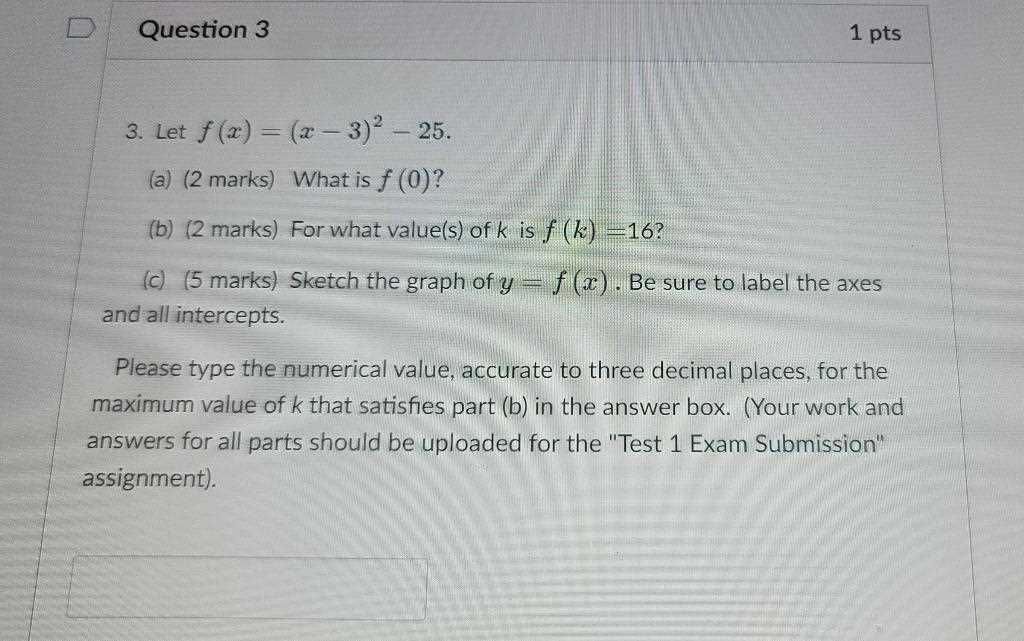
Test Your Knowledge with Practice Questions

Practicing regularly with sample scenarios is an essential part of mastering any subject. By engaging with hypothetical problems and case studies, you can apply your understanding, refine your problem-solving skills, and identify areas that need further attention. This process helps reinforce learning and builds confidence for tackling similar challenges in a real-world setting.

To assess your grasp of key concepts, it is crucial to practice regularly and analyze your approach to each problem. Below are some examples of scenarios to help you get started:

Practice Problems

• Problem 1: A company has recorded the sales data for the past 12 months. How would you calculate the average sales per month, and what statistical measures can help assess sales variability?
• Problem 2: Given a dataset of employee performance ratings, how would you identify any potential outliers? Which technique would you use to detect these anomalies?
• Problem 3: How do you assess the correlation between two variables such as advertising spend and sales volume? What tools or formulas would you use to determine the strength of this relationship?
• Problem 4: In a given experiment, you have two groups: one receives a treatment, and the other does not. What type of hypothesis test would you apply to evaluate the treatment’s effectiveness?
• Problem 5: You are given a dataset showing customer ratings for various products. How would you analyze the distribution of scores and determine the central tendency for this dataset?

Review Your Solutions

• Once you’ve worked through the problems, review your solutions thoroughly to ensure that you applied the correct principles.
• Check if your calculations are consistent and if the conclusions you draw from the data are valid.
• Identify any areas where you encountered difficulty and seek additional resources or practice to improve.

By regularly testing your knowledge with these practice scenarios, you can strengthen your understanding and prepare for challenges ahead. Engaging with a variety of problem types ensures that you develop a well-rounded skill set, enabling you to approach real-world situations with greater ease and accuracy.

Analyzing Past Exam Papers

Reviewing previous assessments is a highly effective strategy for understanding the structure and types of challenges you may face. By analyzing past tests, you can identify recurring themes, common problem types, and areas that are frequently emphasized. This process not only helps familiarize you with the format but also allows you to develop effective strategies for approaching various types of tasks.

To maximize the benefits of this review, focus on understanding both the content and the methods required to solve each problem. Pay close attention to the following aspects:

• Problem Patterns: Look for common topics or recurring problem types. This helps you anticipate which concepts are likely to be tested again.
• Time Management: Assess how much time was allocated to each task and determine how long you should spend on similar problems. This will help you manage your time efficiently.
• Answer Structure: Note the expected format for responses, such as whether short answers, detailed explanations, or calculations are required.
• Difficulty Levels: Gauge the level of difficulty for different sections and determine which areas you need to focus on more intensively.

Incorporating past assessments into your study routine helps you build confidence and refine your approach to complex problems. It also gives you insight into how to allocate your time and energy during real assessments, ensuring you’re well-prepared when the time comes.