Geometry S2 Final Exam Answers and Study Guide

As you approach the end of your academic journey in mathematics, it’s crucial to understand the core principles that will be tested. The skills you need to excel are built upon a foundation of logical reasoning and problem-solving techniques that can be applied to various types of questions.

To ensure you’re well-prepared, it’s important to focus on both theoretical understanding and practical application. Familiarizing yourself with common problem types and refining your approach will help boost your confidence and improve your performance. Knowing how to break down complex problems into manageable parts is essential for achieving the best possible results.

Geometry S2 Final Exam Answers

Achieving success in this stage of your mathematical studies requires more than just memorizing formulas. It’s about mastering a set of skills that can be applied across a range of problems. Whether you’re dealing with intricate diagrams or abstract concepts, understanding the underlying principles is essential for making the right decisions when solving tasks.

The key to excelling lies in familiarity with common types of challenges and how to approach them. By practicing a variety of problems, you can improve your ability to quickly identify patterns and apply the most efficient methods. This approach will help you navigate through any difficulty with greater precision and speed.

Ultimately, developing a clear strategy for problem-solving and being prepared for any variation will give you the best chance to succeed. Whether it’s dealing with proofs, calculations, or visual reasoning, a solid grasp of the core techniques will lead to confident and accurate results.

Understanding the S2 Geometry Exam

To perform well in this section of your studies, it’s important to gain a deeper understanding of the structure and expectations of the assessment. The focus is on applying theoretical knowledge to practical situations, where your problem-solving skills and logical thinking are put to the test. Mastery of key concepts and the ability to adapt them to different scenarios are essential for achieving top results.

Key Areas of Focus

In this stage, certain topics are regularly tested, and becoming familiar with them will provide a significant advantage. Understanding the relationship between shapes, angles, and formulas is crucial for solving problems efficiently. The ability to visualize problems and break them down step-by-step is an essential strategy for success.

Approach to Problem-Solving

When faced with challenges, it’s important to remain calm and methodical. Analyze the problem carefully, identify what’s being asked, and then decide on the most effective approach. Practice with different question types will help you develop a structured method for tackling any task that comes your way.

Key Concepts to Review

Success in this stage relies heavily on a solid understanding of fundamental principles. Focusing on key concepts that form the foundation of more complex problems is crucial. A strong grasp of these ideas will allow you to approach challenges with confidence and precision, as you will be able to apply them to various scenarios effectively.

Focus on mastering the relationships between different geometric elements, such as shapes, angles, and symmetry. Knowing how to calculate areas, perimeters, and volumes, along with understanding the properties of various figures, is essential. Additionally, honing your skills in working with coordinates, transformations, and spatial reasoning will help you tackle more intricate questions.

Lastly, understanding the principles of logical deduction and how to prove statements will strengthen your problem-solving abilities. Being able to clearly articulate reasoning and structure your solutions is just as important as performing calculations accurately.

Common Geometry S2 Mistakes

While preparing for this stage of assessment, it’s essential to be aware of typical errors that many students make. Recognizing these mistakes can help you avoid them and increase your chances of success. Often, these errors stem from a lack of attention to detail or misunderstanding core concepts. By addressing these common pitfalls, you can refine your approach and perform more confidently.

Typical Errors to Avoid

• Misinterpreting the Question: Not fully understanding what is being asked can lead to incorrect methods or solutions.
• Skipping Step-by-Step Reasoning: Rushing through calculations or skipping steps can cause careless mistakes and inaccurate results.
• Incorrect Formula Application: Using the wrong formula or applying it incorrectly can lead to wrong answers. Always double-check the formulas you use.
• Overlooking Units: Forgetting to include or convert units appropriately can throw off your entire solution.
• Neglecting to Review Diagrams: Diagrams provide crucial information that should never be ignored. Ensure you fully analyze them before starting any calculation.
• Not Checking Work: Failing to review your solutions can lead to avoidable mistakes, especially in problems with multiple steps.

How to Avoid These Mistakes

• Read Questions Carefully: Take time to understand every part of the problem before proceeding.
• Break Down Problems: Work through each step methodically and double-check your approach.
• Use the Correct Formulas: Always ensure you are using the right formulas and applying them properly.
• Review Diagrams Thoroughly: Look at all details, such as angles, lengths, and labels, to ensure you are working with the correct information.
• Double-Check Your Work: Always take a few extra minutes to review your calculations and answers to catch any potential mistakes.

How to Prepare Efficiently

Efficient preparation is key to mastering the material and performing well under pressure. Focusing on the most important topics and employing the right strategies will help you maximize your study time and improve your understanding. A well-organized approach, with a mix of practice and review, ensures that you are fully prepared for any challenge that may arise.

To prepare effectively, start by identifying the core concepts that are most likely to appear in the assessment. Once you have a solid understanding of the essential material, practice applying it through various problem types. Time yourself to simulate real conditions and ensure you’re able to complete tasks within the allotted time.

Study Plan Breakdown

Study Focus	Action	Time Allocation
Key Formulas and Theorems	Review essential equations and principles. Understand how and when to use them.	30% of study time
Practice Problems	Work through a variety of problem types to strengthen your skills.	40% of study time
Mock Simulations	Take timed practice tests to improve time management and decision-making under pressure.	20% of study time
Review Mistakes	Analyze any errors you made and ensure you understand why they occurred.	10% of study time

By following a structured study plan and regularly testing your knowledge, you’ll gain the confidence and skills needed to perform at your best.

Tips for Tackling Word Problems

Word problems can be one of the most challenging aspects of this section, as they require not only an understanding of concepts but also the ability to translate text into mathematical operations. The key to solving these problems is breaking them down step by step, identifying the relevant information, and applying the correct methods. With practice and a systematic approach, you can confidently handle even the most complex scenarios.

Step-by-Step Approach

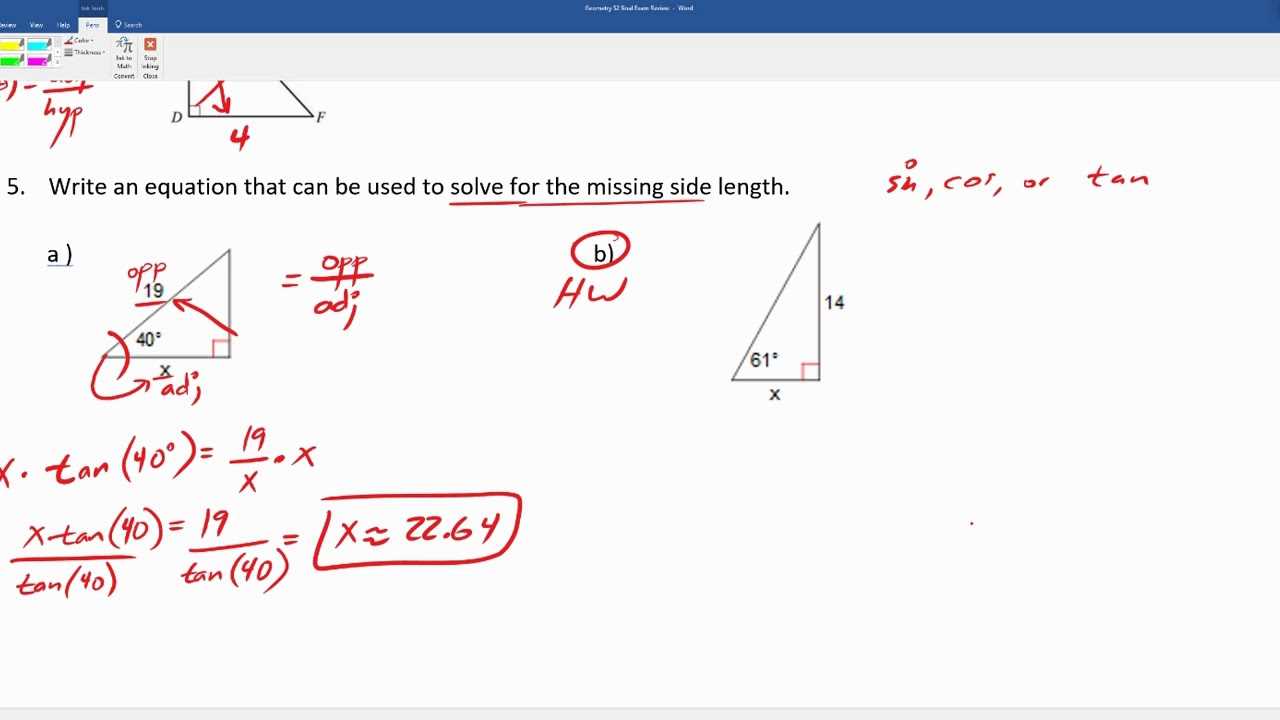
Start by reading the problem carefully, paying attention to every detail. Identify the key facts and translate them into mathematical terms, such as variables or known quantities. Once you have a clear understanding of the given information, determine what the problem is asking you to find and outline the steps necessary to get there.

Common Strategies for Success

• Highlight Important Information: Mark numbers, relationships, and units in the problem statement to ensure nothing is overlooked.
• Set Up Equations: Translate the problem into a solvable equation or system of equations, ensuring each part is connected logically.
• Draw a Diagram: Visualizing the problem can help clarify relationships between elements and make the solution more intuitive.
• Check Your Work: After solving, reread the problem and verify that your solution makes sense in the context of the question.

By following these strategies and staying organized, you will be able to break down word problems more easily and approach them with confidence.

Essential Formulas You Must Know

Having a strong understanding of key formulas is crucial for solving various problems effectively. These formulas serve as the foundation for many tasks, and knowing how and when to apply them can save you time and effort. Mastering these equations will allow you to tackle both simple and complex questions with confidence.

Focus on understanding the relationship between different geometric elements, such as areas, perimeters, volumes, and angles. Memorizing these core equations will provide the tools you need to approach most problems systematically and efficiently.

Key Formulas to Memorize

• Area of a Circle: A = πr² – Used to calculate the area inside a circle.
• Perimeter of a Rectangle: P = 2(l + w) – The sum of all sides of a rectangle.
• Area of a Triangle: A = ½bh – Essential for calculating the area of any triangle.
• Pythagorean Theorem: a² + b² = c² – Used for finding the length of a side in a right triangle.
• Volume of a Rectangular Prism: V = lwh – Formula for calculating the volume of a box-like structure.
• Surface Area of a Sphere: A = 4πr² – Used to find the surface area of a sphere.

By regularly practicing with these formulas and understanding their applications, you’ll be able to solve problems quickly and accurately, making your preparation more efficient.

Practice Problems for Success

One of the most effective ways to reinforce your knowledge and build confidence is by solving practice problems. These exercises help you apply the concepts you’ve learned, identify areas that need improvement, and become comfortable with the format and types of questions you’ll face. Consistent practice ensures you’re ready to handle challenges with ease and accuracy.

Types of Practice Problems

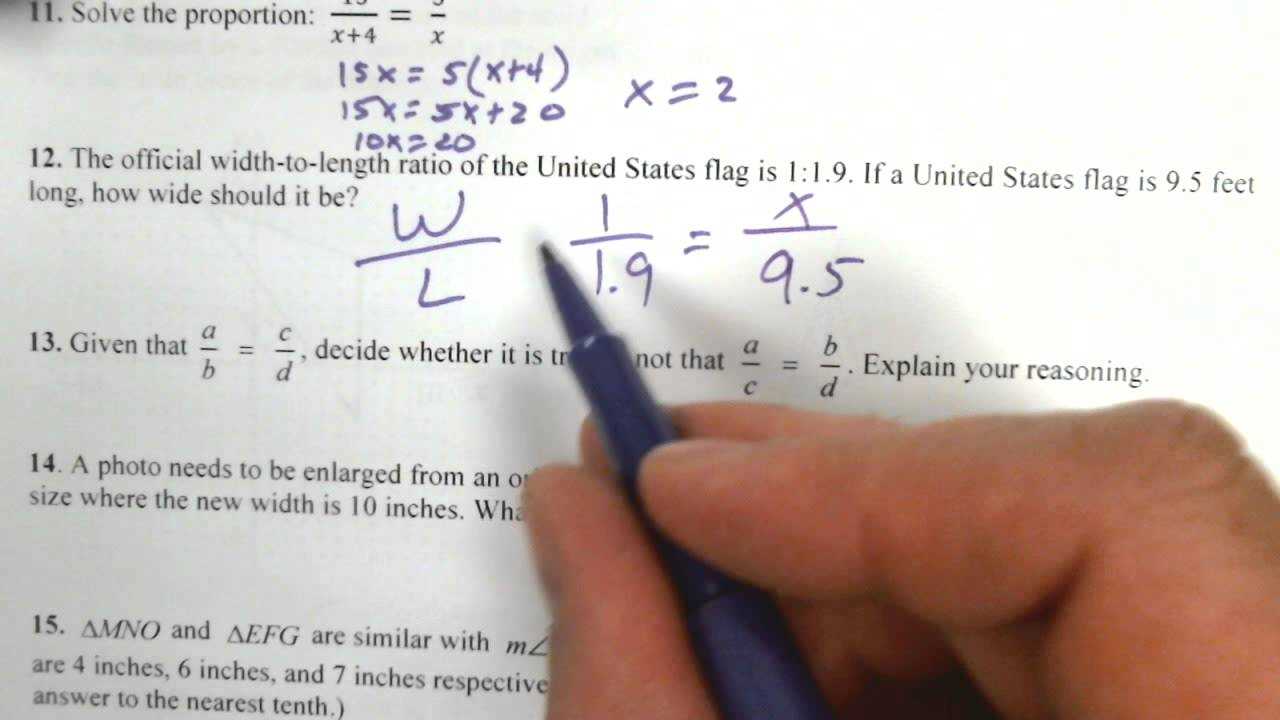
Focusing on a variety of problems will help you build versatility in solving different scenarios. It’s important to not only practice basic calculations but also tackle more complex problems that require multiple steps. Here are some examples of practice problems to help you improve:

• Basic Calculation Problems: These help reinforce foundational skills like solving for areas, volumes, and perimeters.
• Word Problems: These develop your ability to translate real-world scenarios into mathematical equations and solve them logically.
• Proofs and Theorems: Practicing proofs will strengthen your reasoning and understanding of geometric relationships.
• Graphing and Coordinate Geometry: Problems involving coordinates and transformations will improve your spatial reasoning skills.

Maximizing Your Practice

To get the most out of your practice, follow these tips:

• Time Yourself: Try to complete problems within a set time limit to simulate real conditions and improve your time management.
• Review Mistakes: After completing each problem, carefully review your errors to understand what went wrong and learn from them.
• Work in Groups: Discussing problems with peers can provide new perspectives and clarify any confusion.

By regularly practicing and applying these strategies, you’ll be better equipped to solve problems effectively and perform at your best.

Time Management During the Exam

Effective time management is critical to performing well under pressure. When faced with a series of problems, it’s important to balance speed and accuracy to ensure that you can complete all tasks within the allotted time. A strategic approach to how you allocate your time across different sections can make all the difference in achieving a successful outcome.

One of the best ways to manage time effectively is by planning ahead and using your time wisely for each type of question. Prioritize problems based on difficulty, and don’t get stuck on one problem for too long. Keep moving forward to ensure that you give yourself a fair chance to address every question.

Time Allocation Strategy

Section	Recommended Time	Focus Areas
Simple Calculation Problems	30%	Complete these quickly and accurately, focusing on basic equations and formulas.
Word Problems	40%	Carefully read through the problem, extract the relevant information, and set up the correct equations.
Complex or Multi-Step Problems	20%	Work through these step by step, ensuring you don’t miss any critical details.
Review Time	10%	Leave a few minutes to review your answers and correct any mistakes.

By following a structured time management plan, you can improve your efficiency and ensure that you’re able to give your best effort across all sections of the test.

Using Diagrams for Better Accuracy

Diagrams are powerful tools that can significantly enhance your understanding and precision when solving complex problems. Visualizing the problem often makes it easier to grasp relationships between different elements and identify the correct approach. By creating a clear, accurate diagram, you can reduce errors and make the problem-solving process more intuitive.

Whenever you encounter a problem that involves shapes, angles, or spatial relationships, consider drawing a diagram to represent the given information. This step helps organize the details visually, ensuring that nothing is overlooked. Additionally, diagrams can aid in making calculations more straightforward and help you track each step in the process.

Benefits of Using Diagrams

• Clarifies Information: Helps you visualize the relationships between different components, making it easier to apply the correct formulas.
• Reduces Mistakes: Visualizing the problem ensures that you don’t miss important details or misinterpret the given data.
• Simplifies Complex Problems: Breaking down complex problems into a visual representation allows you to focus on one part at a time, preventing confusion.
• Improves Accuracy: Diagrams provide a clear structure that helps you follow the steps correctly and avoid common missteps in the process.

Incorporating diagrams into your problem-solving routine can dramatically improve both the speed and accuracy of your work, making it a critical technique for tackling challenging questions.

Identifying Common Question Types

Recognizing the different types of problems you may encounter allows you to approach them with the right strategy. Each question type often requires a unique method of solving, and by identifying them early, you can allocate your time and energy more efficiently. Understanding these common problem types helps reduce confusion and ensures that you apply the appropriate techniques for each one.

Types of Problems You Might Encounter

• Calculation-Based Problems: These problems typically require you to use formulas to calculate areas, perimeters, volumes, or other related quantities.
• Proof-Based Problems: These questions ask you to logically demonstrate a concept or relationship between geometric elements, often using theorems and postulates.
• Word Problems: Problems presented in written form that describe a scenario requiring you to extract relevant data and translate it into a mathematical equation.
• Transformation Problems: These questions may involve manipulating shapes through various transformations like rotation, reflection, or dilation.
• Coordinate-Based Problems: Problems involving the use of the coordinate plane, where you may need to find distances, midpoints, slopes, or equations of lines.

Approaching Each Problem Type

Once you identify the type of problem, tailor your approach accordingly:

• For Calculation Problems: Ensure that you know all relevant formulas and perform calculations step by step to avoid errors.
• For Proof Problems: Break down the proof into smaller, manageable steps and reference known theorems or axioms to support your argument.
• For Word Problems: Carefully read the entire problem, highlight key information, and translate it into a solvable equation.
• For Transformation Problems: Visualize the shape’s movements and carefully apply transformation rules.
• For Coordinate-Based Problems: Use the coordinate grid to plot points and apply geometric concepts like distance or slope formulas as needed.

By recognizing and understanding these common question types, you’ll be able to solve problems more quickly and with greater accuracy, giving you confidence throughout the test.

What to Do if You’re Stuck

Getting stuck on a challenging problem can be frustrating, but it’s important to remain calm and composed. There are several strategies you can use to regain focus and find a way forward. The key is to approach the problem from different angles, adjust your method if needed, and remember that it’s okay to take a moment to reset your approach.

Steps to Take When You’re Stuck

• Step Back and Breathe: If you’re feeling overwhelmed, take a short break. Step away from the problem for a moment to clear your mind and reduce stress.
• Re-read the Problem: Carefully go over the question again. Often, a second reading will help you notice important details you might have missed the first time.
• Look for Patterns: Try to identify patterns or similarities with problems you’ve solved before. Sometimes applying a familiar method can unlock the solution.
• Work Backwards: Start from the end result or the desired outcome, and see if retracing your steps can help you determine the correct approach.
• Break It Down: Break the problem into smaller, more manageable parts. Solve each part step by step rather than trying to tackle everything at once.

Additional Tips for Getting Unstuck

• Stay Positive: Keep a positive mindset. Stressing about being stuck can hinder your ability to think clearly and find a solution.
• Use a Process of Elimination: If you’re stuck on multiple-choice questions, eliminate obviously incorrect answers first to improve your chances of selecting the correct one.
• Ask for Help (If Available): If you’re really stuck, don’t hesitate to ask for clarification or help from a teacher or fellow student, if permitted.

Remember, getting stuck is a normal part of problem-solving. By using these techniques and maintaining a calm, focused attitude, you’ll increase your chances of overcoming challenges and finishing strong.

Importance of Double-Checking Answers

One of the most valuable habits during any assessment is to review your work before submitting it. Double-checking your solutions can help you catch simple errors, identify overlooked details, and ensure that you’ve used the correct methods. This final step can often be the difference between a good score and a great one.

Why Reviewing Matters

• Catch Calculation Errors: It’s easy to make small arithmetic mistakes or overlook details in complex equations. A second look often helps you spot these issues before they affect your results.
• Ensure Consistency: Re-reading your work ensures that all parts of your solution align with each other and that you haven’t missed any important steps.
• Confirm Correct Application of Methods: Double-checking gives you a chance to ensure you’ve applied the right formulas and techniques throughout the problem-solving process.
• Verify Units and Labels: In problems that involve measurement or specific values, verifying the units used and confirming that labels are correct can save you from costly mistakes.

How to Effectively Review Your Work

• Take Your Time: Don’t rush through your review. Even a few minutes of careful checking can make a big difference.
• Check Key Steps: Focus on the critical steps in your solution. Ensure that each step logically follows from the previous one and that no steps are skipped.
• Use Different Methods: If possible, approach the problem from a different perspective or use an alternate method to confirm the result.

Taking the time to double-check your solutions is a small effort that can significantly improve your performance. By developing this habit, you’ll increase your confidence and accuracy, leading to better outcomes overall.

Strategies for Multiple Choice Questions

Multiple choice questions often present a variety of answer options, and while they may seem straightforward, a strategic approach can significantly improve your chances of selecting the correct response. By applying certain techniques, you can narrow down the choices and increase the accuracy of your answers, even when uncertain.

Effective Approaches for Answering Multiple Choice

• Eliminate Clearly Incorrect Options: Start by removing the answers that are obviously wrong. This increases the likelihood of choosing the correct option from the remaining choices.
• Look for Keywords: Pay attention to keywords in both the question and the answer choices. These can provide hints toward the correct response.
• Consider Each Answer Carefully: Don’t rush through the options. Sometimes, answers may appear similar but contain slight differences that could be key to the solution.
• Work Backwards (If Possible): If you’re unsure, try plugging the answer options back into the question to see which one fits best.
• Don’t Overthink: Trust your initial instincts. Overanalyzing can lead to confusion and second-guessing, which may result in mistakes.

When to Guess and How to Maximize Your Chances

When you’re unsure about a particular question, guessing can still be a viable option, especially if you’ve already narrowed down the choices. Here are a few tips for making an educated guess:

Strategy	Description
Eliminate Extremes	Often, the extreme options (very high or low numbers) are less likely to be correct. Consider this when making a guess.
Pick the Middle Option	If the answers are numerical, the middle value is often a safe bet, as it’s more likely to be the correct answer.
Use Context	Use your understanding of the topic to make a logical guess based on the context of the question.

By applying these strategies, you can increase your chances of selecting the correct answer, even when faced with difficult questions. Proper preparation and careful analysis of the options will give you the edge in answering multiple-choice questions more confidently and accurately.

How to Handle Complex Proofs

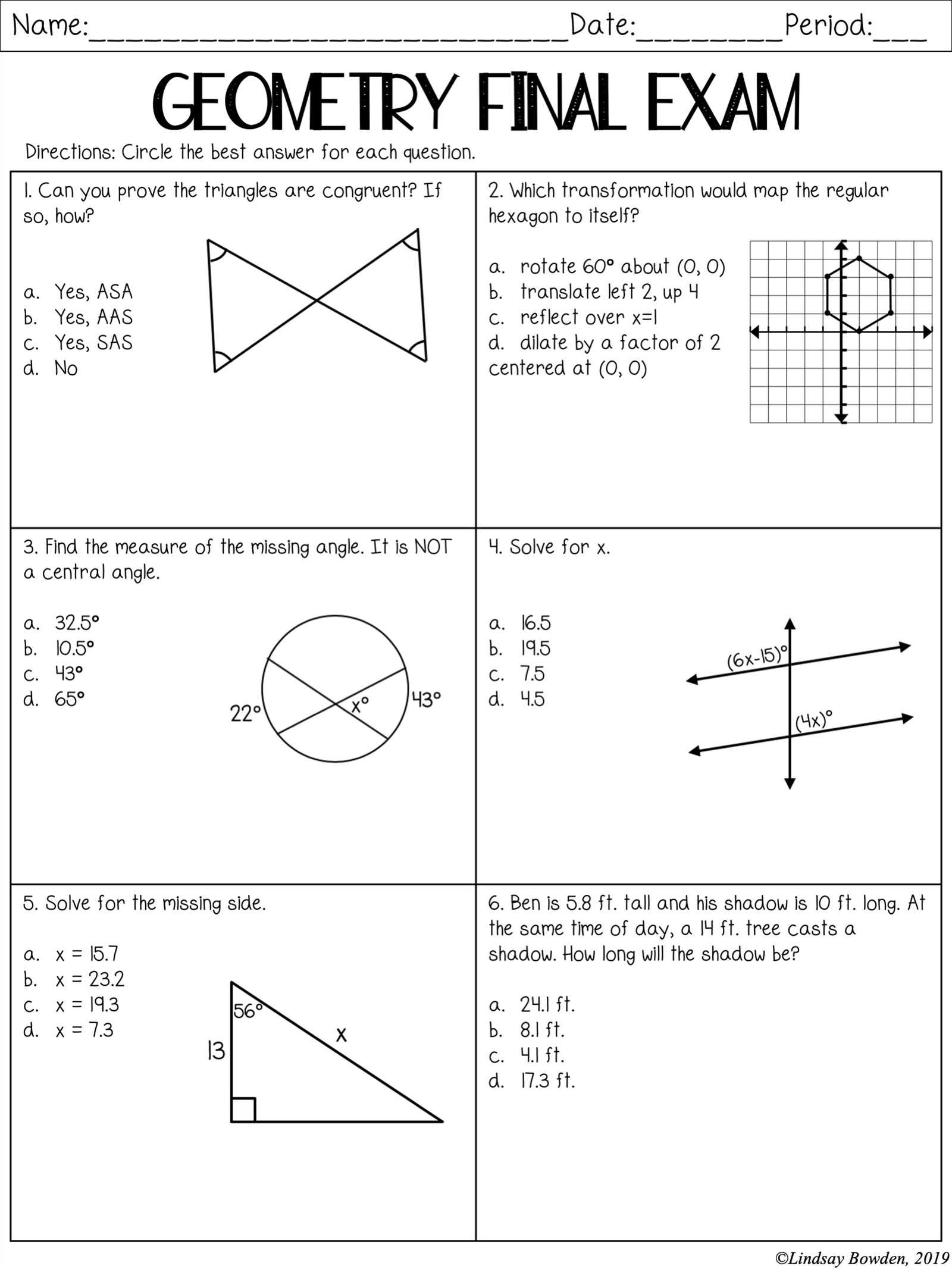
Complex proofs can often feel overwhelming, but with the right approach, they can be broken down into manageable steps. The key is to stay organized and methodical, ensuring that each logical step is properly followed. By understanding the structure of a proof and knowing the strategies to use, you can successfully navigate even the most challenging problems.

Breaking Down the Problem

The first step in tackling a complex proof is to carefully read through the problem. Identify the known information, the goal, and what needs to be proven. Breaking the problem down into smaller parts can make it more manageable. Look for any diagrams or visual aids that can help you understand the relationships between different elements. It’s also useful to recall any relevant properties or theorems that may apply to the situation.

Step-by-Step Approach

• Start with Known Information: Begin by writing down the information you already know. This could include given values, equations, or geometric properties.
• Define Variables: If needed, introduce variables to represent unknown quantities. This can help simplify the process and make the proof more structured.
• Apply Logical Steps: Use logical reasoning to connect your known information to the unknowns. This might involve applying specific theorems, definitions, or algebraic manipulations.
• Stay Organized: Keep track of each step as you go along. Label each part of the proof clearly, whether it’s a statement, justification, or conclusion.
• Conclude with the Goal: Once you’ve reached the end of the proof, make sure your conclusion directly addresses the problem’s objective. Double-check the logic to ensure everything fits together.

By taking a systematic approach and applying a clear, logical structure to the proof, you can handle even the most complex problems with confidence. Practice and familiarity with different types of proofs will help you improve over time.

Reviewing Mistakes for Future Tests

Understanding and analyzing mistakes is one of the most effective ways to improve performance in any assessment. By reviewing errors carefully, you can identify patterns, recognize areas of weakness, and develop strategies for better outcomes in the future. This reflective process is essential for mastering the material and becoming more proficient in problem-solving.

Identifying Common Errors

When reviewing past mistakes, it’s important to categorize the errors. Were they due to misunderstanding a concept, making a simple calculation mistake, or overlooking key information? By grouping mistakes into categories, you can pinpoint the areas that need more focus and practice. Here are some common types of errors:

• Conceptual Mistakes: These occur when the fundamental principles are misunderstood or not applied correctly. For example, misinterpreting a formula or theorem.
• Calculation Mistakes: Simple arithmetic errors or overlooking negative signs can lead to incorrect results.
• Time Management Errors: Rushing through problems without careful thought can lead to overlooked details or incomplete solutions.
• Misreading Questions: Sometimes, the mistake is simply not fully understanding the problem’s requirements, leading to incorrect assumptions.

Using Mistakes to Improve

Once the errors are identified, the next step is to focus on improving in those specific areas. Here are a few strategies:

• Revisit Key Concepts: Spend time reviewing the concepts where mistakes occurred. Reinforce your understanding through additional practice problems and explanations.
• Practice More Problems: Doing a variety of similar problems helps to strengthen your grasp on weak areas and reduces the likelihood of repeating the same mistakes.
• Seek Help When Needed: If a concept remains unclear, don’t hesitate to ask for help. Whether from a teacher, tutor, or peer, getting clarification can prevent future mistakes.
• Simulate Testing Conditions: Practice solving problems under timed conditions to improve both accuracy and speed.

By turning mistakes into learning opportunities, you not only improve your understanding but also boost your confidence for the next assessment. Reviewing mistakes thoroughly will make you more prepared and efficient in the long run.

Staying Calm and Focused on Exam Day

Maintaining composure and concentration on the day of an assessment is crucial for performing at your best. Anxiety and distractions can easily take a toll on your performance, but with the right approach, you can stay focused and navigate through the tasks with clarity. It’s important to implement strategies that help you remain calm and ensure you approach each question with a clear mindset.

Pre-Assessment Preparation

How you prepare before the day of the test can play a significant role in how you feel during it. Here are some steps you can take to minimize stress and increase your focus:

• Get Plenty of Rest: A good night’s sleep is essential for your brain to function optimally. Rest helps with memory retention and cognitive function.
• Eat a Balanced Meal: Eating a healthy breakfast ensures your body has the energy needed to maintain focus throughout the session. Avoid sugary or heavy foods that could cause a sugar crash.
• Arrive Early: Arriving at the location with plenty of time allows you to settle in, calm your nerves, and review any last-minute materials without rushing.

During the Assessment

Once the assessment begins, staying calm and focused is essential for completing the tasks efficiently. Follow these tips to maintain your concentration:

• Start with Easy Questions: Tackling the simpler questions first can help build confidence and warm up your brain before tackling more difficult ones.
• Take Deep Breaths: If you start feeling anxious or overwhelmed, take a few deep breaths. This helps reduce stress and brings your focus back to the task at hand.
• Work at Your Own Pace: While time is important, don’t rush through the questions. Read each one carefully and take your time to think through the steps needed to find a solution.
• Stay Positive: Don’t dwell on mistakes or tough questions. If you don’t know the answer to a question, move on and return to it later if needed.

By preparing properly and staying calm and focused throughout the assessment, you can maximize your chances of success. Keeping a level head will help you think clearly and approach each challenge with confidence.